A light rod of length of length 2m is suspended from a ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross - section 10−3m2 and the other is of brass of cross- section 2×10−3m2.x is the distance from the steel wire end, at which a weight may be hung. Ysteel=2×1011PaandYbrass=1011Pa
Which of the following statement(s) is /are correct ?
The correct Answer is:A, B, C
To solve the problem, we need to analyze the forces acting on the rod and the conditions for equilibrium. We will follow these steps:
Step 1: Understand the Setup
We have a horizontal rod of length 2 m suspended by two vertical wires: one made of steel and the other made of brass. The cross-sectional areas are given, and we need to find the point x from the steel wire end where a weight can be hung such that the stresses in both wires are equal.
Step 2: Define the Variables
- Let TS be the tension in the steel wire.
- Let TB be the tension in the brass wire.
- The cross-sectional area of steel wire AS=10−3m2.
- The cross-sectional area of brass wire AB=2×10−3m2.
- Young's modulus for steel YS=2×1011Pa.
- Young's modulus for brass YB=1011Pa.
Step 3: Apply the Condition of Equal Stress
Since the stresses in both wires are equal, we have:
TSAS=TBAB
Substituting the areas:
TS10−3=TB2×10−3
This simplifies to:
TB=2TS(1)
Step 4: Apply the Condition of Equilibrium
For the rod to be in equilibrium, the sum of moments about any point must be zero. Taking moments about the point where the brass wire is attached (let's call this point B):
TS⋅x=TB⋅(2−x)
Substituting TB from equation (1):
TS⋅x=2TS⋅(2−x)
Dividing both sides by TS (assuming TS≠0):
x=2(2−x)
Expanding this gives:
x=4−2x
Rearranging gives:
3x=4⟹x=43m≈1.33m
Step 5: Conclusion
The distance x from the steel wire end at which a weight may be hung such that the stresses in both wires are equal is approximately 1.33m.
We have a horizontal rod of length 2 m suspended by two vertical wires: one made of steel and the other made of brass. The cross-sectional areas are given, and we need to find the point x from the steel wire end where a weight can be hung such that the stresses in both wires are equal.
- Let TS be the tension in the steel wire.
- Let TB be the tension in the brass wire.
- The cross-sectional area of steel wire AS=10−3m2.
- The cross-sectional area of brass wire AB=2×10−3m2.
- Young's modulus for steel YS=2×1011Pa.
- Young's modulus for brass YB=1011Pa.
Since the stresses in both wires are equal, we have:
TSAS=TBAB
Substituting the areas:
TS10−3=TB2×10−3
This simplifies to:
TB=2TS(1)
For the rod to be in equilibrium, the sum of moments about any point must be zero. Taking moments about the point where the brass wire is attached (let's call this point B):
TS⋅x=TB⋅(2−x)
Substituting TB from equation (1):
TS⋅x=2TS⋅(2−x)
Dividing both sides by TS (assuming TS≠0):
x=2(2−x)
Expanding this gives:
x=4−2x
Rearranging gives:
3x=4⟹x=43m≈1.33m
The distance x from the steel wire end at which a weight may be hung such that the stresses in both wires are equal is approximately 1.33m.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Exercise 15.14videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Exercise 15.22videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Solved Examples6videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions469videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
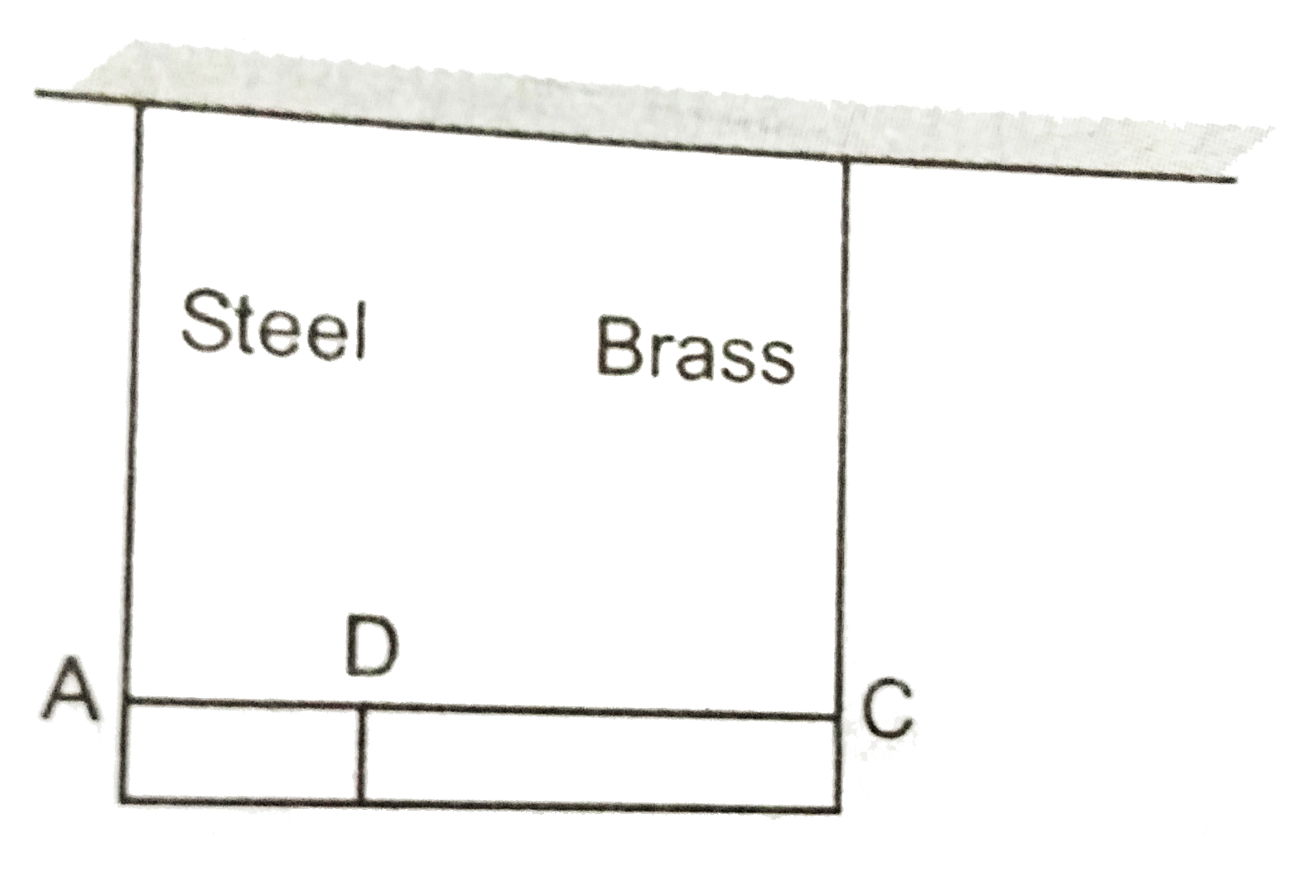
A light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]
 View Solution
View SolutionA light rod of length 2m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross section 0.1cm2. The other wire is a brass of cross section 0.2cm2. A weight is suspended from a certain point of the rod such that equal stress are produced in both the wires. Which of the following are correct?
View Solution
Knowledge Check
- Question 1 - Select One
A light rod of length 2 m is suspended from ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 0.1 cm sq. and the other of brass of cross-section 0.2 cm sq. Along the rod at what distance a weight may be hung to produce equal stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wire
A 2 m long light metal rod AB is suspened form the c eiling horizontally by means of two vertices wires of equal length, tied to the ends. One brass and has corss section of 0.3×10−4m2 and the other is of steel with 0.1×10−4m2 corss-section. In order to have equal stresses in the two wires, a weight is hung from the rod. The position of weight along the rod from end A should be.
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
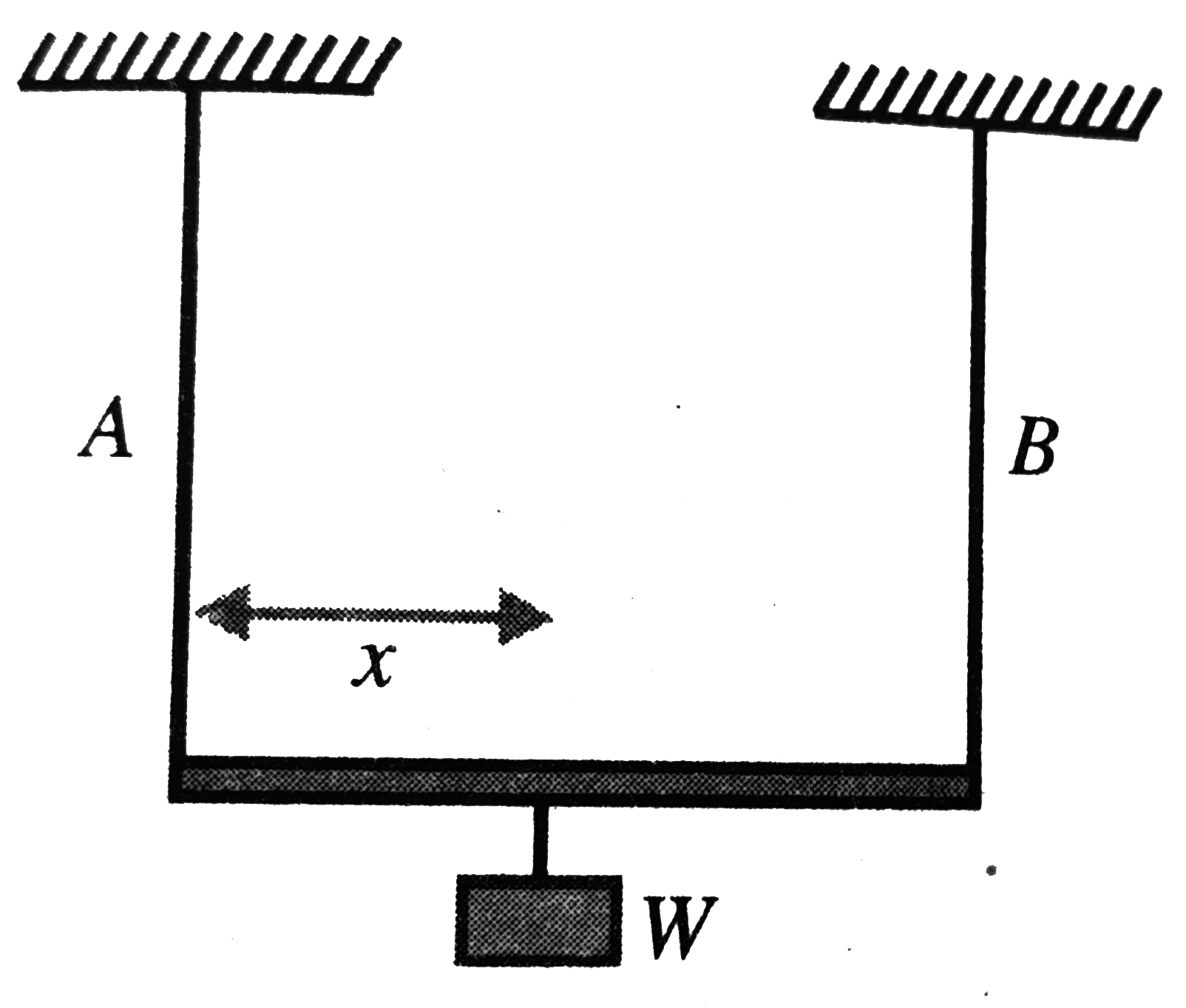
Determine the value of x so that equal stresses are produced in each wire.View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
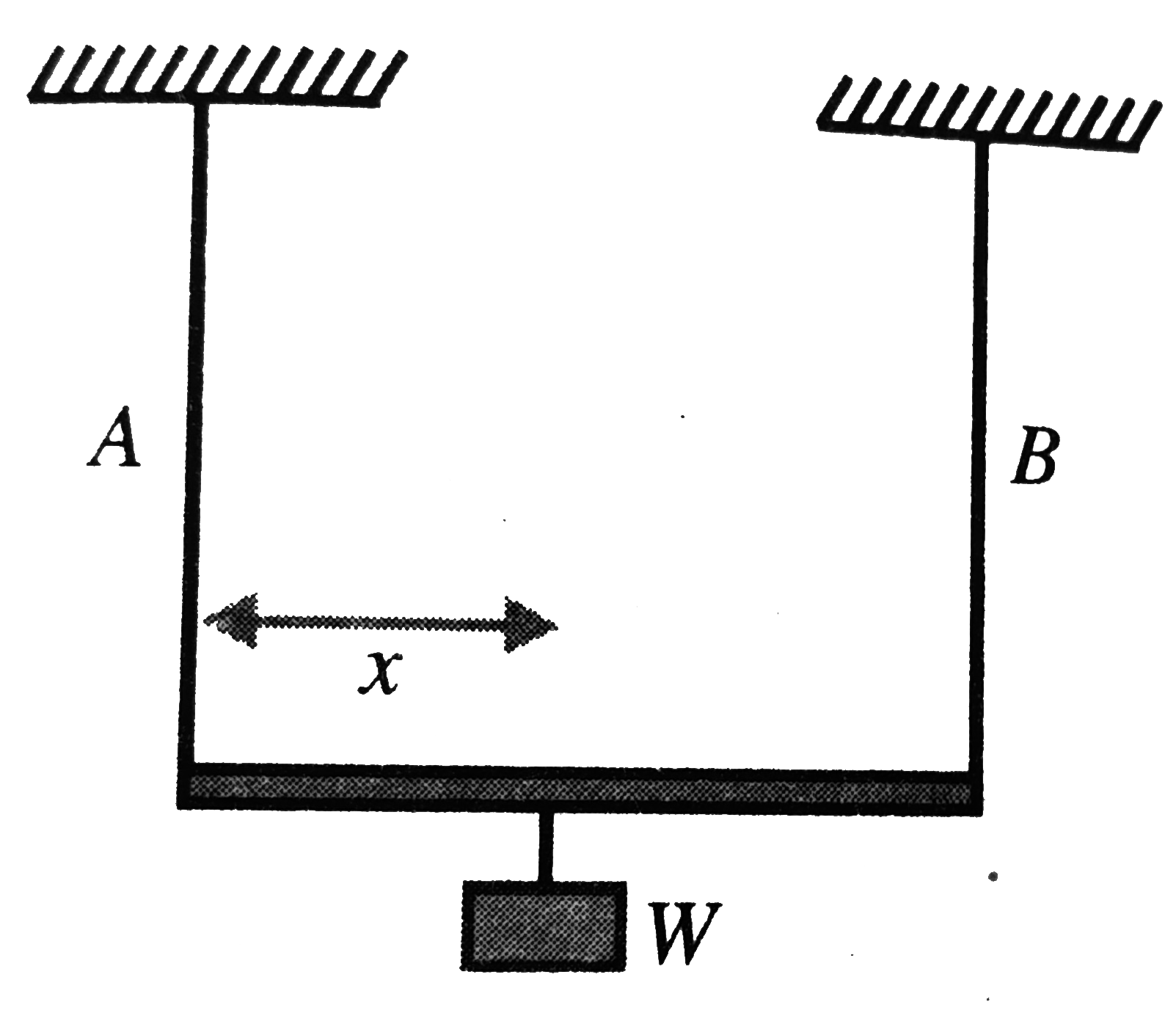
Determine the value of x so that equal strains are produced in each wireView SolutionA copper wire of cross - sectional area 3.4 mm2 and length of the wire 400m, specific resistivity of copper is 1.7×10−8Ω−m. Then the resistance of the wire is
View SolutionDetermine the force required to double the length of the steel wire of area of cross-section 5×10−5m2. Give Y for steel =2×1011Nm−2.
View SolutionFour wires of equal length 2 m are arranged as shown in the figure. Wires , 2, 3 and 4 are of equal cross-sectional area and wire 1 is of half the cross section of these wires. By how much distance pointer at point 5 must be moved to get null point ?
 View Solution
View SolutionA steel wire 2m long is suspended from the ceiling. When a mass is hung from its lower end, the increase in length recorded is 1cm. Determine the strain in the wire.
View Solution

