Question

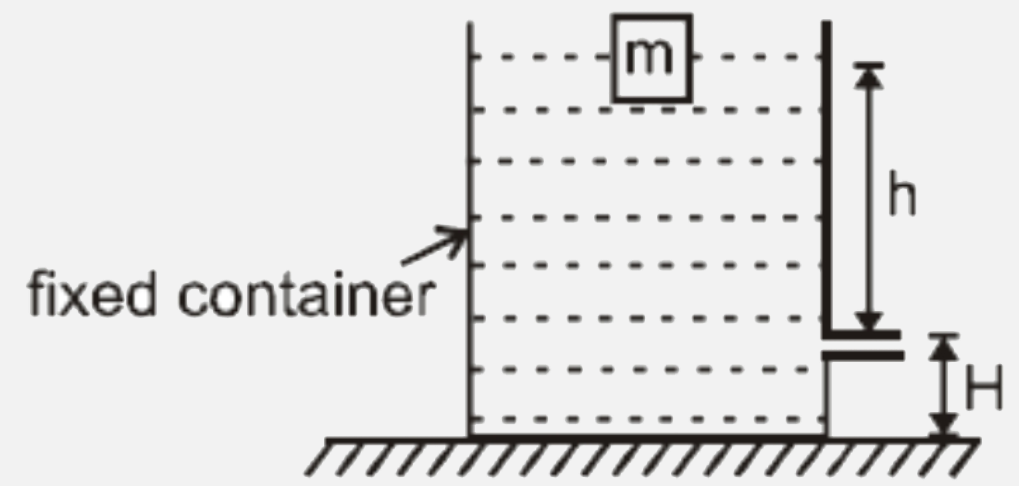
A solid sphere of radius $R$ made of a material of bulk modulus $B$ is surrounded by a liquid in a cylindrical container. $A$ massless piston of area $A$ (the area of container is also $A$) floats on the surface of the liquid. When a mass $M$ is placed on the piston to compress the liquid , fractional change in radius of the sphere is $\frac{Mg}{\alpha AB}$. Find the value of $\alpha$.

Answer

C

Explanation

To solve the problem step by step, we need to analyze the situation involving a solid sphere submerged in a liquid, surrounded by a piston. Here’s the solution:

Step 1: Understand the System
We have a solid sphere of radius \( R \) made of a material with bulk modulus \( B \). The sphere is surrounded by a liquid in a cylindrical container, and a mass \( M \) is placed on a massless piston that floats on the liquid.

Step 2: Determine the Change in Pressure
When the mass \( M \) is placed on the piston, it exerts a force on the liquid, creating a change in pressure (\( \Delta P \)). The change in pressure can be calculated as:
\( \Delta P = \frac{F}{A} = \frac{Mg}{A} \)
where \( g \) is the acceleration due to gravity and \( A \) is the area of the piston.

Step 3: Relate Bulk Modulus to Pressure and Volume Change
The bulk modulus \( B \) is defined as:
\( B = -\frac{\Delta P}{\frac{\Delta V}{V}} \)
Rearranging gives:
\( \frac{\Delta V}{V} = -\frac{\Delta P}{B} \)

Step 4: Substitute the Change in Pressure
Substituting the expression for \( \Delta P \) into the bulk modulus equation:
\( \frac{\Delta V}{V} = -\frac{\frac{Mg}{A}}{B} = -\frac{Mg}{AB} \)
Taking the absolute value, we have:
\( \left| \frac{\Delta V}{V} \right| = \frac{Mg}{AB} \)

Step 5: Relate Volume Change to Radius Change
The volume \( V \) of a sphere is given by:
\( V = \frac{4}{3} \pi R^3 \)
The change in volume \( \Delta V \) can be expressed in terms of the change in radius \( \Delta R \):
\( \Delta V = V' - V = \frac{4}{3} \pi (R + \Delta R)^3 - \frac{4}{3} \pi R^3 \)
Using the binomial expansion for small changes, we can approximate:
\( \Delta V \approx 4 \pi R^2 \Delta R \)
Thus:
\( \frac{\Delta V}{V} \approx \frac{4 \pi R^2 \Delta R}{\frac{4}{3} \pi R^3} = \frac{3 \Delta R}{R} \)

Step 6: Set the Two Expressions for Volume Change Equal
From the previous steps, we have:
\( \frac{Mg}{AB} = \frac{3 \Delta R}{R} \)
Rearranging gives:
\( \Delta R = \frac{MgR}{3AB} \)

Step 7: Find the Fractional Change in Radius
The fractional change in radius is given by:
\( \frac{\Delta R}{R} = \frac{Mg}{3AB} \)

Step 8: Compare with Given Expression
The problem states that the fractional change in radius is also given by:
\( \frac{Mg}{\alpha AB} \)
By comparing the two expressions:
\( \frac{Mg}{3AB} = \frac{Mg}{\alpha AB} \)
This implies:
\( \alpha = 3 \)

Final Answer
Thus, the value of \( \alpha \) is:
\( \alpha = 3 \)