A uniform copper bar of density ρ , length L , cross - sectional area S and young's modulus Y is moving horizontally on a frictionless surface with constant acceleration a0. Find
(a) the stress at the center of the wire ,
(b) total elongation of the wire .
The correct Answer is:A, C, D
To solve the problem step by step, we will find the stress at the center of the copper bar and then calculate the total elongation of the wire.
Step 1: Understanding the Problem
We have a uniform copper bar with:
- Density: ρ
- Length: L
- Cross-sectional area: S
- Young's modulus: Y
- Acceleration: a0
The bar is moving horizontally on a frictionless surface with constant acceleration a0.
Step 2: Finding the Stress at the Center of the Wire
1. Identify the forces acting on the bar:
- The tension in the bar due to the acceleration can be considered. The total mass of the bar is m=ρ⋅V=ρ⋅(S⋅L).
2. Divide the bar:
- Consider the left half of the bar, which has a length of L2 and a mass of m2.
3. Calculate the tension (T):
- The tension at the center of the bar due to the acceleration is given by:
T=m2⋅a0=ρSL2⋅a0
4. Calculate the stress:
- Stress is defined as force per unit area. Therefore,
Stress=TS=ρSL2⋅a0S=ρLa02
Step 3: Finding the Total Elongation of the Wire
1. Consider a small element of the wire:
- Take a small segment of the wire of length dx at a distance x from one end.
2. Calculate the tension at this segment:
- The tension in this segment is given by:
T(x)=mL⋅x⋅a0=ρSLL⋅x⋅a0=ρSa0x
3. Calculate the elongation of the small segment dx:
- The elongation dL of the small segment is given by:
dL=T(x)⋅dxY⋅S=ρSa0x⋅dxY⋅S=ρa0x⋅dxY
4. Integrate to find the total elongation:
- The total elongation ΔL of the entire wire is obtained by integrating dL from 0 to L:
ΔL=∫L0ρa0x⋅dxY=ρa0Y∫L0x⋅dx=ρa0Y⋅(x22)L0=ρa0L22Y
Final Answers
(a) The stress at the center of the wire is:
Stress=ρLa02
(b) The total elongation of the wire is:
ΔL=ρa0L22Y
We have a uniform copper bar with:
- Density: ρ
- Length: L
- Cross-sectional area: S
- Young's modulus: Y
- Acceleration: a0
1. Identify the forces acting on the bar:
- The tension in the bar due to the acceleration can be considered. The total mass of the bar is m=ρ⋅V=ρ⋅(S⋅L).
- Consider the left half of the bar, which has a length of L2 and a mass of m2.
- The tension at the center of the bar due to the acceleration is given by:
T=m2⋅a0=ρSL2⋅a0
- Stress is defined as force per unit area. Therefore,
Stress=TS=ρSL2⋅a0S=ρLa02
1. Consider a small element of the wire:
- Take a small segment of the wire of length dx at a distance x from one end.
- The tension in this segment is given by:
T(x)=mL⋅x⋅a0=ρSLL⋅x⋅a0=ρSa0x
- The elongation dL of the small segment is given by:
dL=T(x)⋅dxY⋅S=ρSa0x⋅dxY⋅S=ρa0x⋅dxY
- The total elongation ΔL of the entire wire is obtained by integrating dL from 0 to L:
ΔL=∫L0ρa0x⋅dxY=ρa0Y∫L0x⋅dx=ρa0Y⋅(x22)L0=ρa0L22Y
(a) The stress at the center of the wire is:
Stress=ρLa02
ΔL=ρa0L22Y
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.1
15 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.2
15 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Comprehension Based
6 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A smooth uniform, string of natural length l, cross-sectional area A and Young’s modulus Y is pulled along its length by a force F on a horizontal surface. Find the elastic potential energy stored in the string.
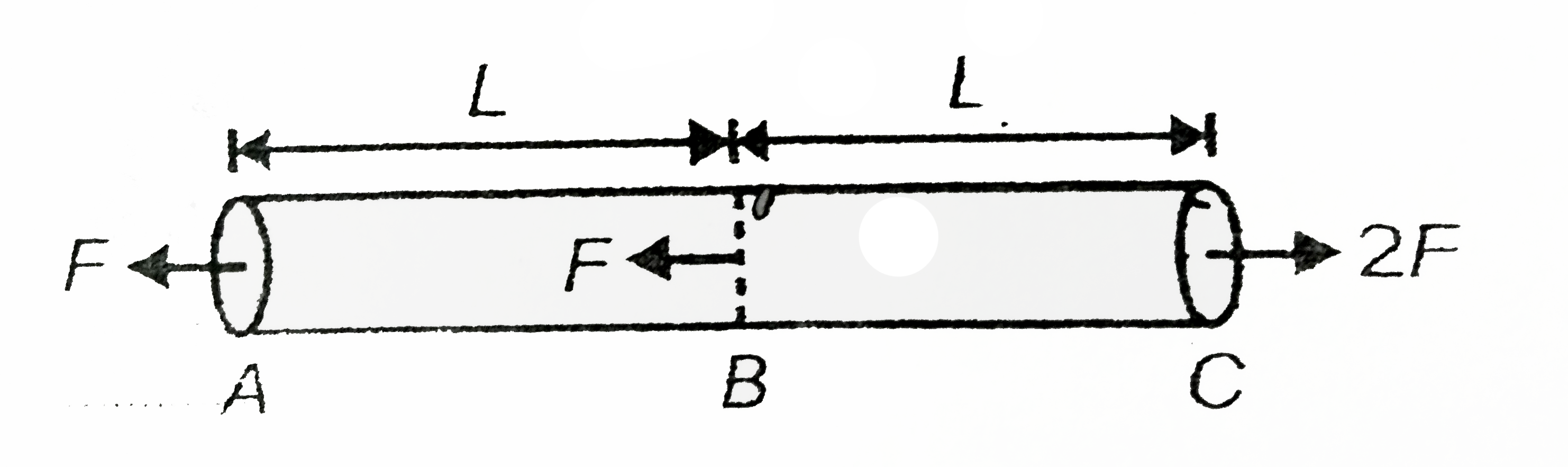
View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
View Solution
Knowledge Check
A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2LA cord of mass m length L, area of cross section A and Young's modulus y is hanging from a ceiling with the help of a rigid support. The elogation developed in the wire due to its own weight is
Aμgl2YABμgl22YAC2μgl2YAD2μgl23YA
A uniform rod of length l, mass m, cross-sectional area A and Young's modulus Y is rotated in horizontal plane about a fixed vertical axis passing through one end, with a constant angular velocity ω. Find the total extension in the rod due to the tension produced in the rod.
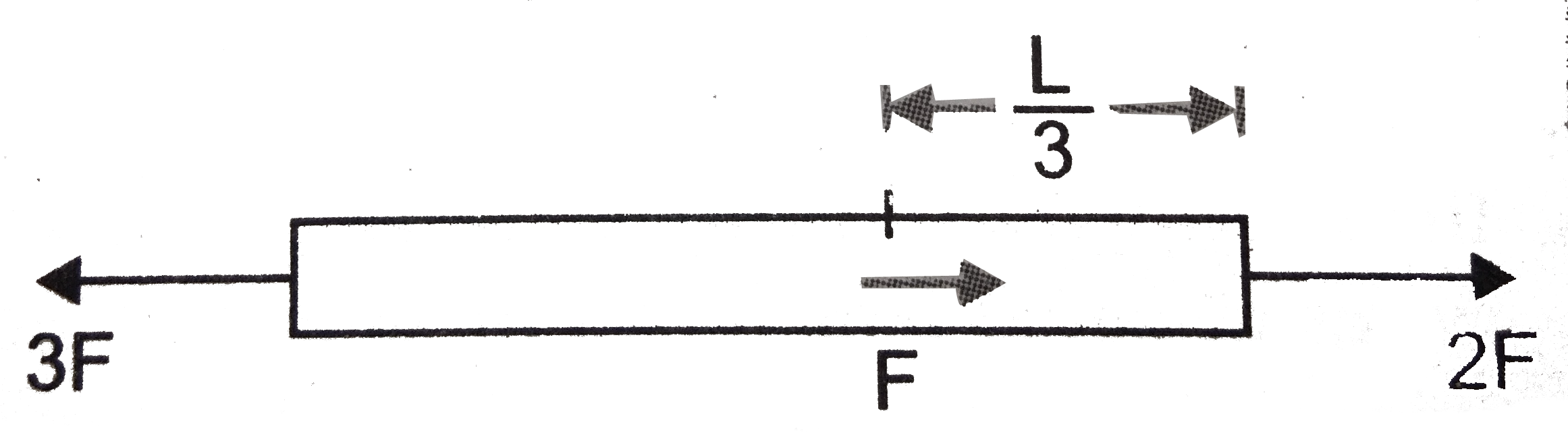
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
Select the correct alternatives.
View SolutionA metal wire of length L, area of cross-section A and young's modulus Y is stretched by a variable force F such that F is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is l
View SolutionA wire of uniform cross-sectional area A and young's modulus Y is stretched within the elastic limits. If s is stress in the wire, the elastic energy density stored in the wire in terms of the given parameters is
View SolutionA ring of radius R is made of a thin wire of material of density ρ, having cross-section area a and Young's modulus y. The ring rotates about an axis perpendicular to its plane and through its centre. Angular frequency of rotation is ω.
The tension in the ring will be
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View Solution
