A metallic sphere floats in an immiscible mixture of water (ρw=103kg/m3) and a liquid (ρL=13.5×103kg/m3) such that its 45th volume is in water and 15th volume in the liquid. Find the density of metal.
The correct Answer is:A, C
To solve the problem, we need to apply the principle of buoyancy, which states that the weight of the fluid displaced by the submerged part of the sphere is equal to the weight of the sphere itself.
1. Identify the given values:
- Density of water, ρw=103kg/m3
- Density of liquid, ρL=13.5×103kg/m3
- Volume of the sphere submerged in water, Vw=45V
- Volume of the sphere submerged in the liquid, VL=15V
2. Calculate the buoyant force:
The buoyant force is equal to the weight of the fluid displaced by the submerged parts of the sphere. This can be calculated as:
Fb=Weight of water displaced+Weight of liquid displaced
Fb=(Vw⋅ρw⋅g)+(VL⋅ρL⋅g)
Substituting the volumes:
Fb=(45V⋅ρw⋅g)+(15V⋅ρL⋅g)
3. Substitute the densities:
Fb=(45V⋅103⋅g)+(15V⋅13.5×103⋅g)
4. Factor out common terms:
Fb=V⋅g(45⋅103+15⋅13.5×103)
5. Calculate the total buoyant force:
Fb=V⋅g(4⋅103+13.5×1035)
Fb=V⋅g(4+13.55×103)=V⋅g(17.55×103)
Fb=V⋅g(3.5×103)
6. Weight of the sphere:
The weight of the sphere is given by:
W=V⋅ρm⋅g
where ρm is the density of the metal.
7. Set the buoyant force equal to the weight of the sphere:
V⋅g(3.5×103)=V⋅ρm⋅g
8. Cancel out common terms (V and g):
3.5×103=ρm
9. Final answer:
ρm=3.5×103kg/m3
Conclusion:
The density of the metal sphere is ρm=3.5×103kg/m3.
- Density of water, ρw=103kg/m3
- Density of liquid, ρL=13.5×103kg/m3
- Volume of the sphere submerged in water, Vw=45V
- Volume of the sphere submerged in the liquid, VL=15V
The buoyant force is equal to the weight of the fluid displaced by the submerged parts of the sphere. This can be calculated as:
Fb=Weight of water displaced+Weight of liquid displaced
Fb=(Vw⋅ρw⋅g)+(VL⋅ρL⋅g)
Substituting the volumes:
Fb=(45V⋅ρw⋅g)+(15V⋅ρL⋅g)
Fb=(45V⋅103⋅g)+(15V⋅13.5×103⋅g)
Fb=V⋅g(45⋅103+15⋅13.5×103)
Fb=V⋅g(4⋅103+13.5×1035)
Fb=V⋅g(4+13.55×103)=V⋅g(17.55×103)
Fb=V⋅g(3.5×103)
The weight of the sphere is given by:
W=V⋅ρm⋅g
where ρm is the density of the metal.
V⋅g(3.5×103)=V⋅ρm⋅g
3.5×103=ρm
ρm=3.5×103kg/m3
The density of the metal sphere is ρm=3.5×103kg/m3.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
21 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A metallic sphere floats in immiscible mixture of water (density 103kgm−3) and a liquid (density 8×103kgm−3) such that its (2/3) part is in water and (1/3) part in the liquid. The density of the metal is
View SolutionA cube of 1 kg is floating at the interface of two liquids of density ρ1=3/4gm/cm3andρ2=2.5gm/cm3 The cube has (3/5)th part in ρ2 and (2/5)th part in ρ1 .Find the density of the cube .

View Solution
Knowledge Check
A metallic sphere floats in an immiscible mixture of water (ρW=103kg/m3) and a liquid (ρ1=13.5×103kg/m3) such that is (4/5) th portion is in water and (1/5) th portion in the liquid. The density of metal is
A4.5×103kg/m3B4.0×103kg/m3C3.5×103kg/m3D1.9×103kg/m3A vessel contains two immiscible liquids of density ρ1=1000kg/m3 and ρ2=1500kg/m3. A solid block of volume V=103m3 and density d=800kg/m3 is tied to one end of a string and the outer end is tied to the bottom of the vessel as shown in figure.
The block is immersed with two fifths of its volume in the liquid of lower density. The entire system is kept in an elevator which is moving upwards with an acceleration of a=g2. Find the tension in the string. A1. 8NB2. 6NC3. 10ND4. 12N
A1. 8NB2. 6NC3. 10ND4. 12N
A tank is filled with water of density 103kg/m3 and oil of density 0.9×103kg/m3.The height of water layer is 1m and that of the oil layer is 4M. The velocity of efflux front an opening in the bottom of the tank is
View SolutionTwo immisible liquids are pured in a U-tube having densities ρ1=1.0×102kg/m2andρ23.0×102kg/m3. Find the ratio of heights (of the liquids above their interface) n1h2

View SolutionWhat fraction of an iceberg ice beneath the surface of the sea? Density of sea water (ρ)=1.028×103kg/m3, density of ice d. =0.917×103kg/m3
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
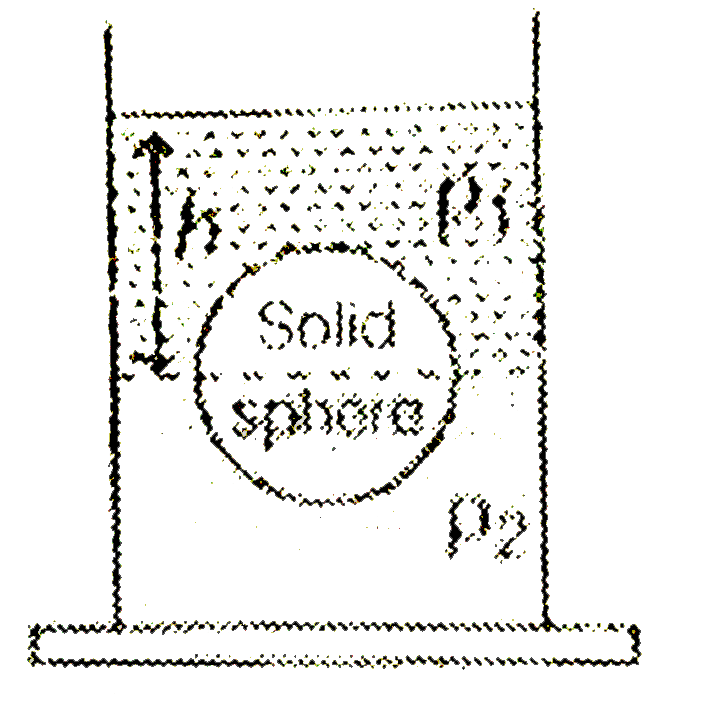
View SolutionA cubical tank of side 1 m is filled with 800 kg of a liquid. Find the density of liquid in kg m−3
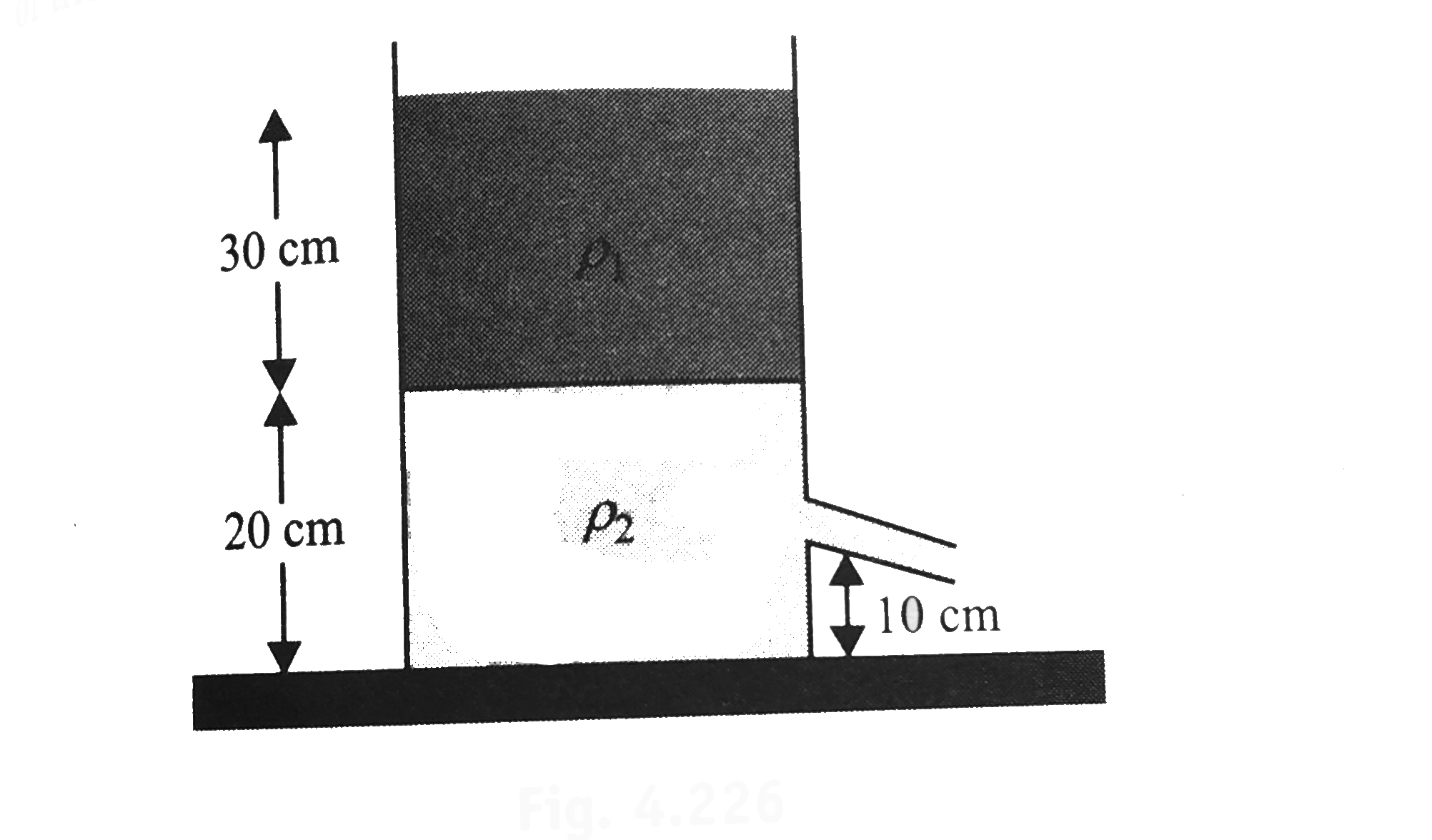
View SolutionA cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density ρ1=600kg/m3 and ρ2=1200kg/m3 as shown in the figure.
A small hole having cross sectional area 5cm2 is made in right side vertical wall as shown. Take atmospheric pressure as p0=105N/m2,g=10m/s2. For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as 1000cm2. Neglect the mass of the vessel.
View Solution
