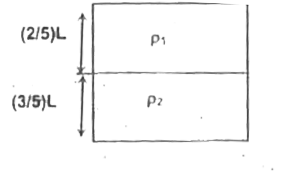
A cube of 1 kg is floating at the interface of two liquids of density ρ1=3/4gm/cm3andρ2=2.5gm/cm3 The cube has (3/5)th part in ρ2 and (2/5)th part in ρ1 .Find the density of the cube .

The weight of the cube = (force acting by the liquid of density ρ1) + (force acting by the liquid of density of ρ2)
Let mass of the block = m
mg=v1ρ1g+v2ρ2g
⇒(ApL)={A(2/5)L}ρ1g+v2ρ2g
⇒(AρL)={A(2/5)L}ρ1+{A(3/5)L}ρ2
⇒=2ρ1+3ρ26
⇒ρ=2(3/4)+3(2.5)5=1.5+7.55=1.8gmcm3
Similar Questions
A metallic sphere floats in an immiscible mixture of water (ρw=103kg/m3) and a liquid (ρL=13.5×103kg/m3) such that its 45th volume is in water and 15th volume in the liquid. Find the density of metal.
View SolutionThe light cone is in equilibrium under the action of hydrostatic forces of two liquids of densities ρ1 and ρ2. Find ρ1/ρ2. Find ρ1 and ρ2.

View Solution
Knowledge Check
A metallic sphere floats in an immiscible mixture of water (ρW=103kg/m3) and a liquid (ρ1=13.5×103kg/m3) such that is (4/5) th portion is in water and (1/5) th portion in the liquid. The density of metal is
A4.5×103kg/m3B4.0×103kg/m3C3.5×103kg/m3D1.9×103kg/m3
A solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
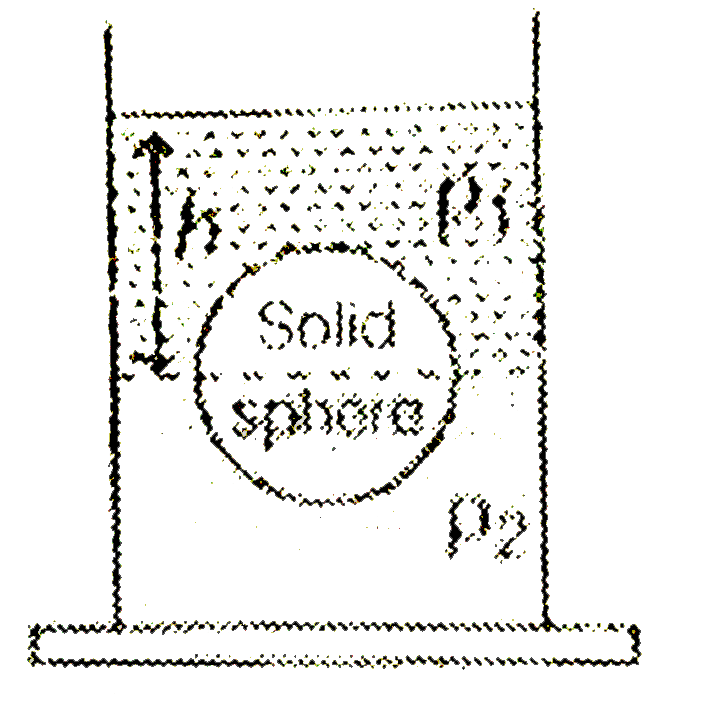
View SolutionA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
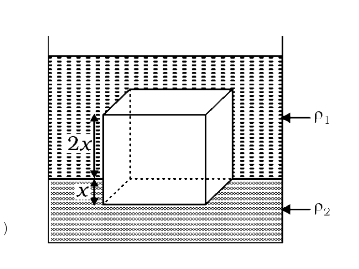
View SolutionA cubical block of density ρ floats completely immersed in two non-mixing liquids of densities ρ1andρ2 as shown in figure. The relation between ρ,ρ1andρ2 is :
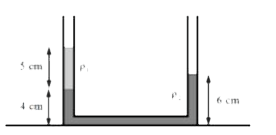
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
View SolutionA solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

View SolutionA rectangular tube of uniform cross section has three liquids of densities ρ1,ρ2 and ρ3. Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density ρ1 in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane.

View Solution
