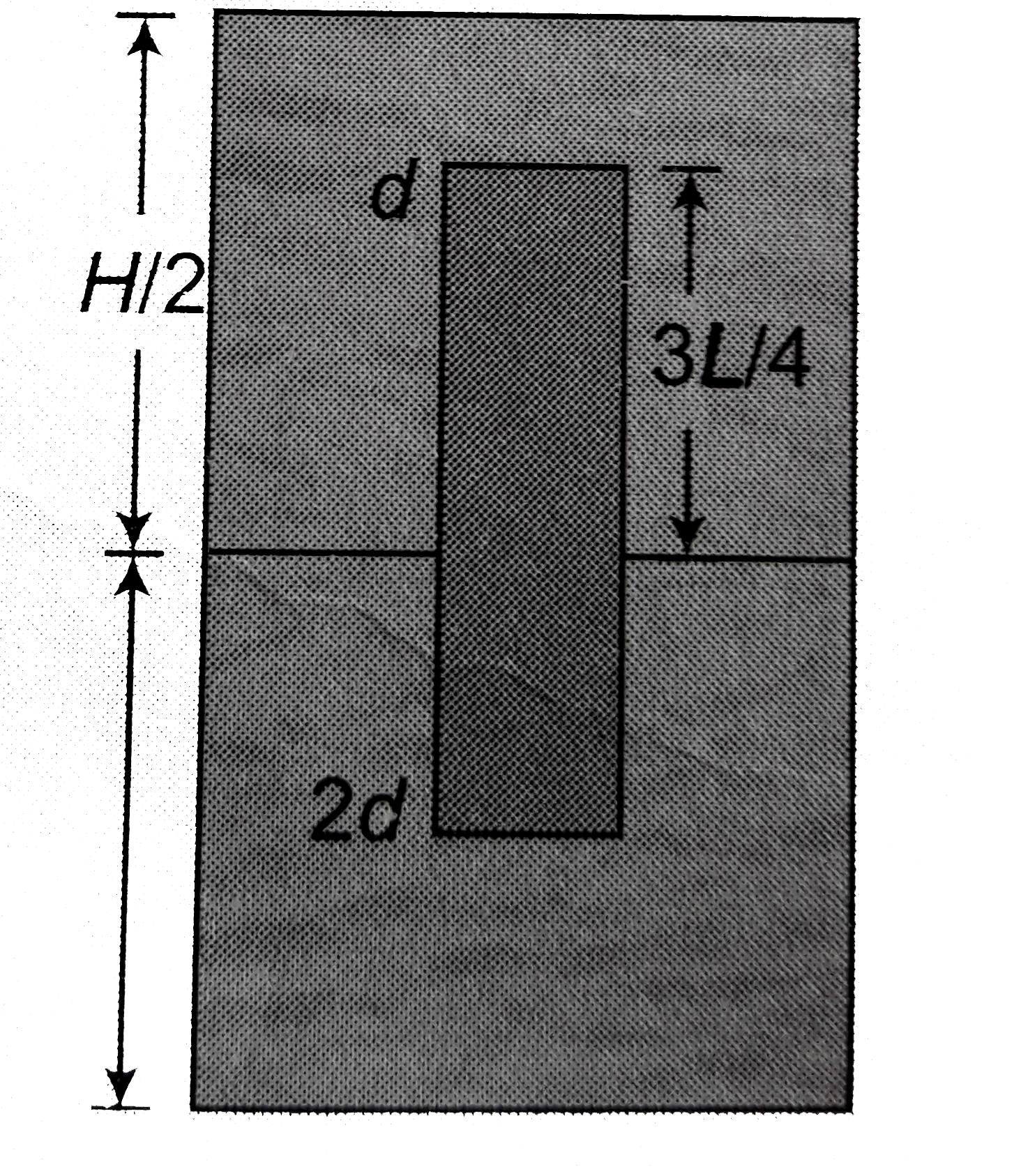
A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height as shown in the figure. The lower density liquid is open to the atmosphere having pressure . A homogeneous solid cylinder of length and cross-sectional area is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length in the denser liquid,

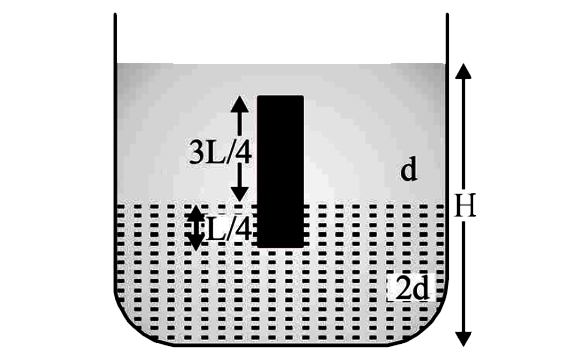
The cylinder is then removed and the original arrangement is restroed. a tiny hole of area is punched on the vertical side of the container at a height . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
The correct Answer is:B
weight of two liquids + weight of cylinder
.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective24videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.11videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct10videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial value of x isView SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,
The density D of the material of the floating cylinder is View Solution
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L<H2), cross-sectional area A/5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L/4 denser liquid. Determine
(a) density D of the solid and
(b) the total pressure at the bottom of the container. (Atmospheric pressure =P0).
 .View Solution
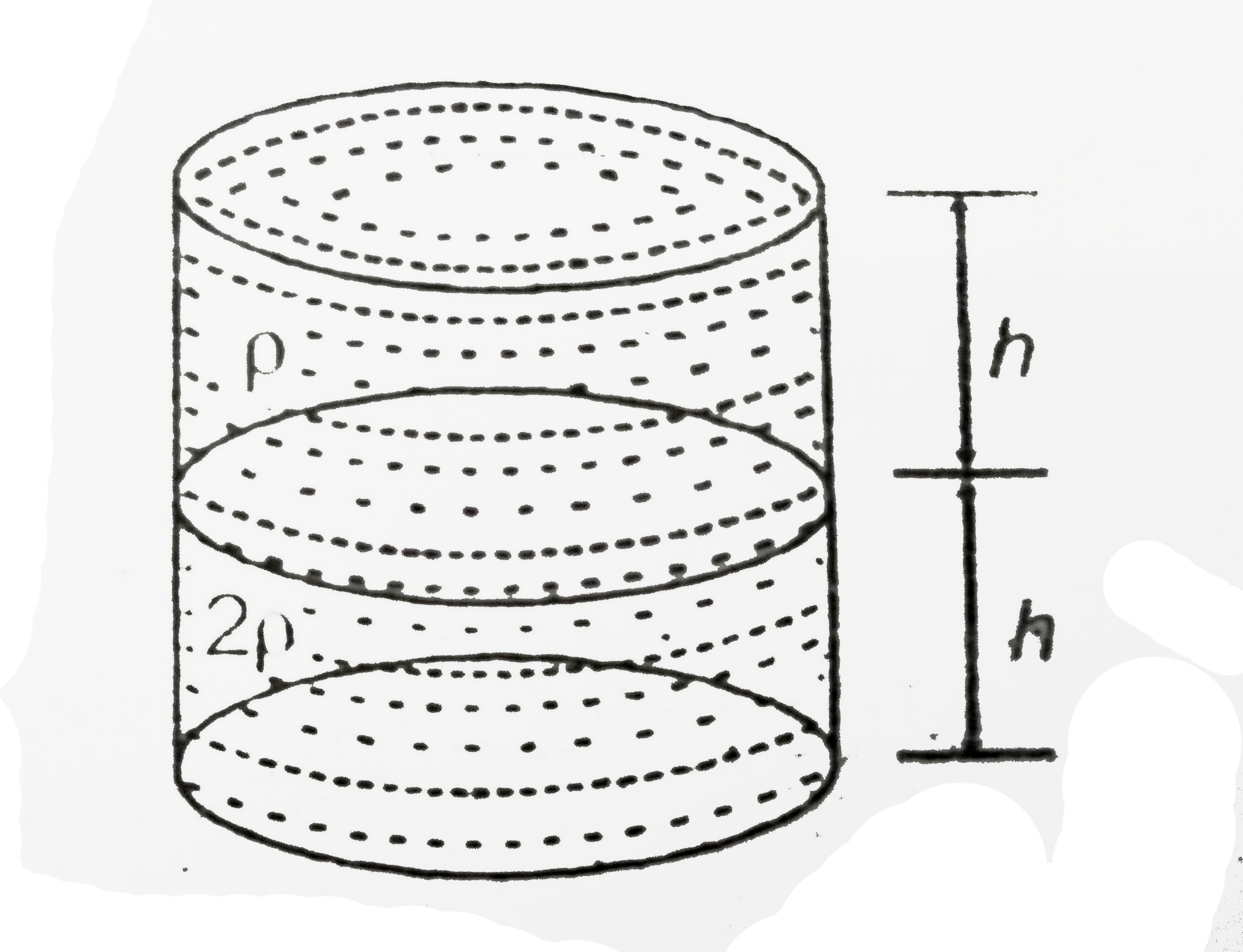
.View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
 View Solution
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
 View Solution
View SolutionA container of large uniform cross sectional area A, resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density d and 2d, each of height H2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area (s(s<<A) is punched on the vertical side of the container at a height h(h<H2). Determine

the initial speed of efflux of the liquid at the holeView SolutionA container of large uniform cross sectional area A, resting on horizontal surface, holds two immiscible non viscous and incompressible liquids of density d and 2d, each of height H2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area (s(s<<A) is punched on the vertical side of the container at a height h(h<H2). Determine

The horizontal distance traveled by the liquid, initially, is :View SolutionA container of large uniform cross sectonal area A, resting on horizontal surface, holds two immiscible non viscous and incompresible liquids of density d and 2d, each of height H2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H2). Determine

a.the initial speed of efflux of the liquid at the hole
b. the horizontal disance x travelled by the liquid initially
c. the height hm at which at the hole should be punched so that the liquid travels the maximum distance xm initially. also calculate xm (neglect air resistance inte calculations).View SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation I:
A homogeneous solid cylinder of length L(L<H/2). cross sectional area A/5 is immersed such that it floats with its axis vertical at liquid -liquid interface with lenght L/4 in the denser liquid.
The total pressure at the bottom of the container isView SolutionFluids at rest exert a normal force to the walls of the container or to the sruface of the body immersed in the fluid. The pressure exerted by this force at a point inside the liqid is the sum of atmospheric pressure and a factor which depends on the density of the liquid, the acceleration due to gravity and the height of the liquid, above that point. The upthrust acting on a body immersed in a stationary liquid is the net force acting on the body in the upward direction. A number of phenomenon of liquids in motion can be explain by Bernoulli's theorem which relates the pressure, flow speed and height for flow of an ideal incompressible fluid.
A container of large uniform corss sectional area. A resting on a horizontal surface holds two immiscible, non viscous and incompressile liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
Situation II:
A cyliner is removed and the original arrangement is restoreed.A tiny hole of area s(s<<A) is punched on the veritical side of the containier at a height h(h<H/2)
The height hm at which the hole should be punched so that the liquid travels the maximum distance isView Solution

