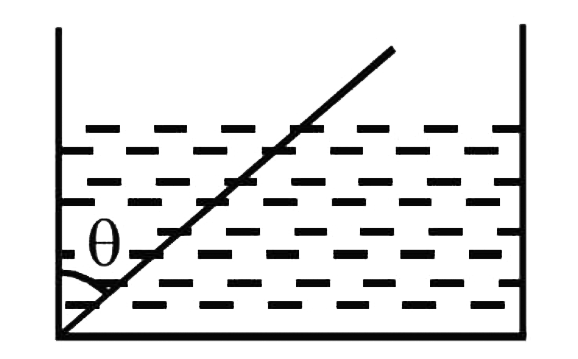
A wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
The correct Answer is:D
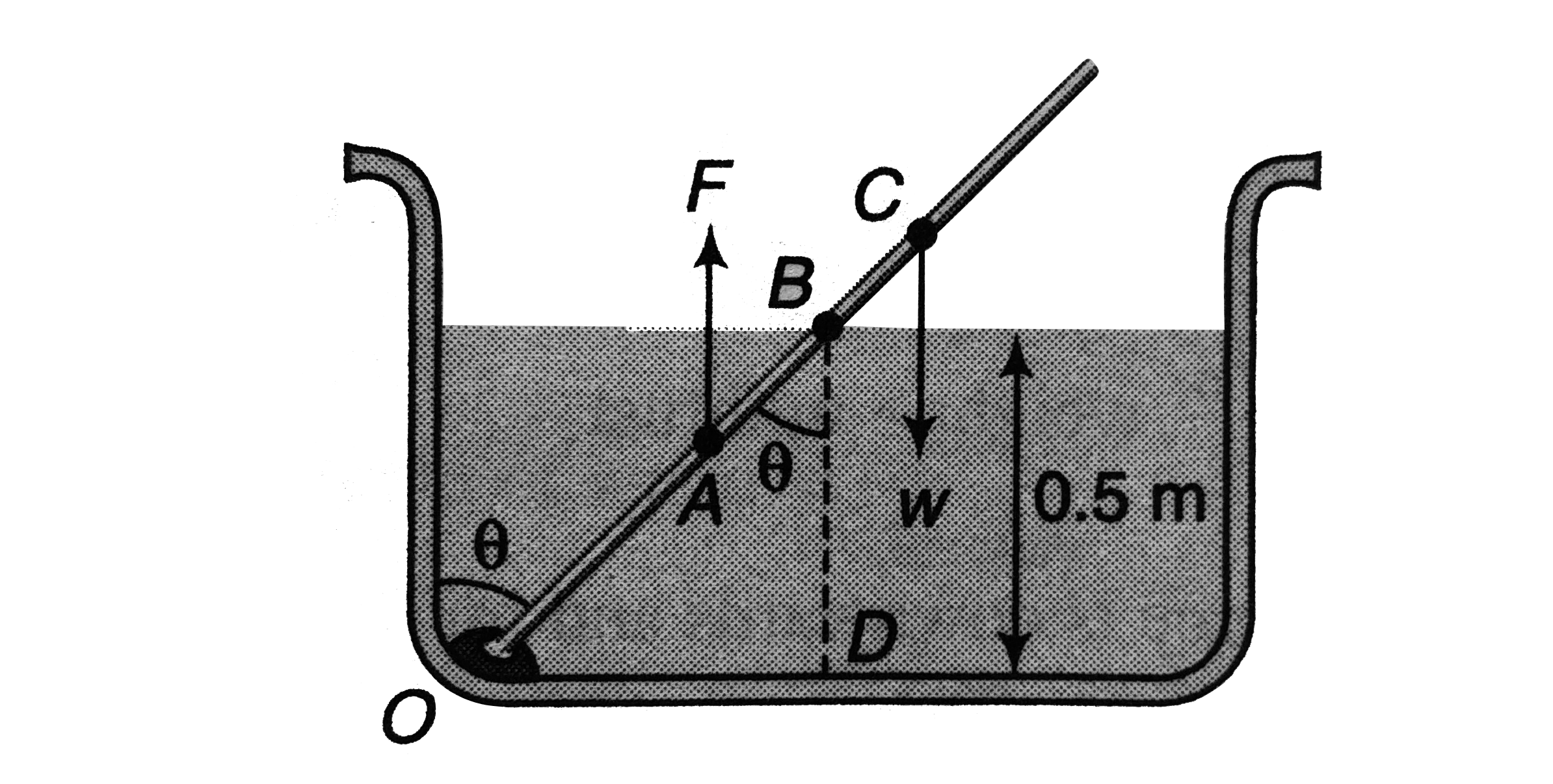
OA=OB2=0.5secθ2=0.25sec(θ)
About point O, clockwise moment of
w= anticlockwise moment of F.
∴w(L2sinθ)=F(OAsinθ)=F(0.25sinθ.secθ)
Given, L=1m
∴cosθ=F2w=(0.5secθ)(A)(1.0)g2(1)(A)(0.5)g
or, cos2θ=12,cosθ=1√2
∴θ=45∘
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.1
1 Video
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.2
1 Video
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
The wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,
,
View SolutionA wooden rod of a uniform cross section and of length 120cm is hinged at the bottom of the tank which is filled with water to a height of 40cm. In the equilibrium position, the rod makes an angle of 60∘ with the vertical. The centre of buoyancy is located on the rod at a distance (from the hinge) of
View Solution
Knowledge Check
A liquid of density ρ0 is filled in a wide tank to a height h. A solid rod of length L, cross-section A and density ρ is suspended freely in the tank. The lower end of the rod touches the base of the tank and h=L/n (where n gt 1). Then the angle of inclination θ of the rod with the horizontal in equilibrium position is
Asin−1(√ρ0ρ)Bsin−1(n√ρ0ρ)Csin−1(1n√ρ0ρ)Dsin−1(1n√ρρ0)
Two non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
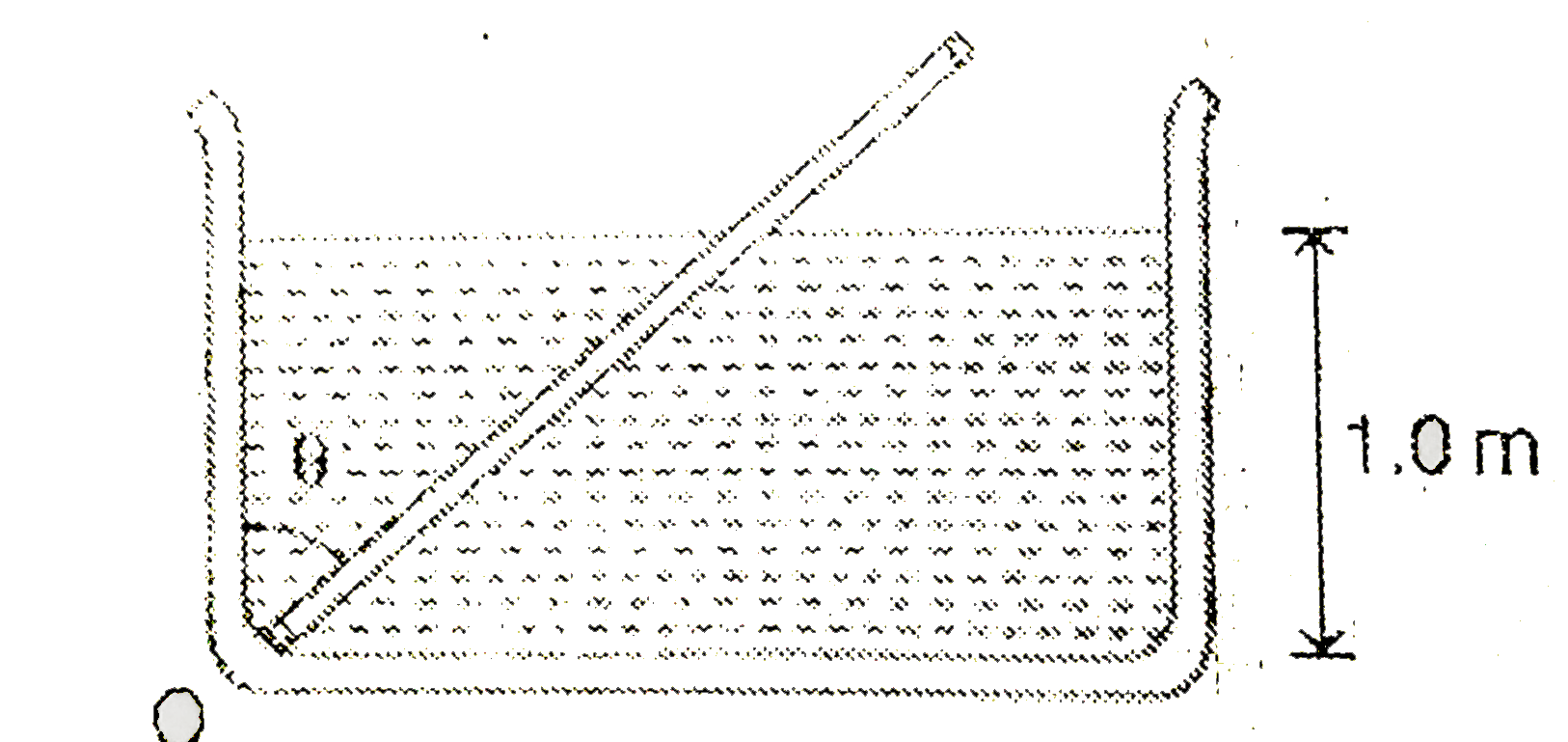
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
View SolutionA tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
View SolutionA uniform wooden bar of length l and mass m hinged on a vertical wall of a containing water, at one end.

3/5th part of the bar is submerged in water. Find the ratio of densities of the liquid and the bar.
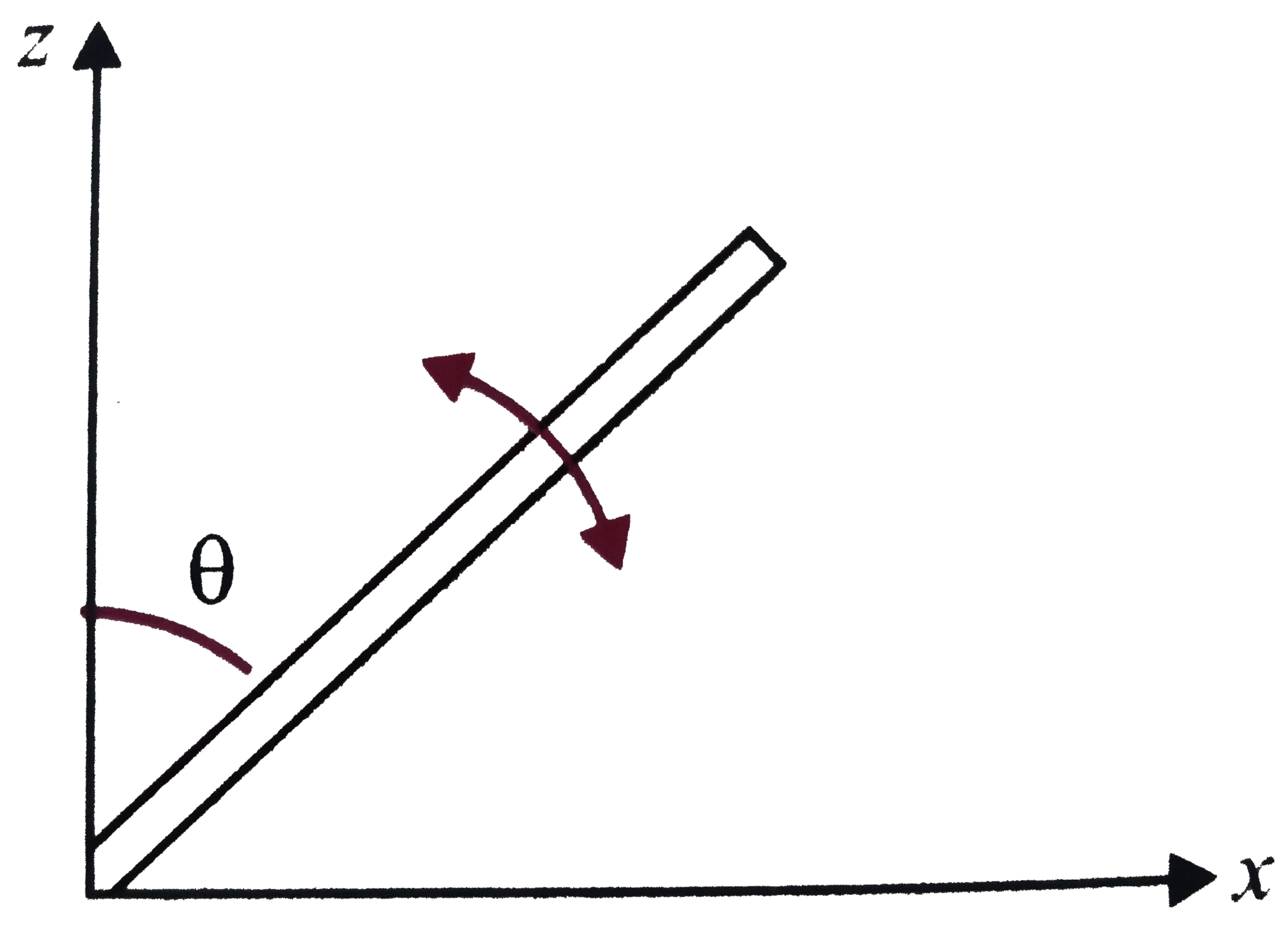
View SolutionA slender uniform rod of mass M and length l is pivoted at one end so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
View SolutionAn L shaped uniform rod of mass 2M and length 2L(AB=BC=L) is held as shown in Fig. with a string fixed between C and wall so that AB is vertical and BC is horizontal. There is no friction between the hinge and the rod at A.

If the string is burnt, find the angle between AB and the vertical at equilibrium position.
View SolutionA large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular path which lies in a horizantal plane. The length of the string from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
View Solution