A ball of density d is dropped on to a horizontal solid surface. It bounces elastically from the surface and returns to its original position in a time t1. Next, the ball is released and it falls through the same height before striking the surface of a liquid of density of dL
(a) If d<dL, obtain an expression (in terms of d, t1 and dL) for the time t2 the ball takes to come back to the position from which it was released.
(b) Is the motion of the ball simple harmonic?
(c) If d=dL, how does the speed of the ball depend on its depth inside the liquid? Neglect all frictional and other dissipative forces. Assume the depth of the liquid to be large.
The correct Answer is:A, B, C, D
In elastic collision with the surface, direction of velicity is reversed but its magnitude remains the same,
Therefore, time of fall=time of rise,
or, time of fall =t12
Hence, velocity of the ball just before it collides with liquids is
v=g(t1)2
Retardation inside the liquid
a=upthrust-weightmass=VdLg−VdgVd
=(dL−dd)g
Time taken to come to rest under this retardation will be
t=va=gt12a=gt12(dL−dd)g
=dt12(dL−d)
Same will be the time to come to back on the liquid surface.
therefore,
(a) (t2)= time the ball takes to came back to the position from where it was released
=t1+2t=t1+dt1dL−d
=t1[1+ddL−d] or t2=t1dLdL−d
(b) The motion of the ball is periodic but not simple harminic because the acceleration of the ball is g in air and (dL−dd)g inside the liqudi which is not proportional to the displacenent, which is necessary and sufficient condition for SHM.
(c ) When (dL=d), retardation or acceleration inside teh liquid becones zero (upthrust-weight). Therefore, the ball will continue to move with constant velocity v=>12 inside the liquid.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.11videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Example 13.21videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based7videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
A ball of density ρ is dropped from a height on the surface of a non-viscous liquid of density 2ρ. Choose the correct options.
 View Solution
View SolutionA ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. A. What are the initial and final kinetic energies of the ball? b. What is the work done by the kinetic friction?
View SolutionA ball is dropped at t=0 from a height on a elastic surface. Identify the gragh which correctly represents relation of kinetic energy K with time t.
View SolutionA small ball is dropped from a certain height on the surface of a non-viscous liquid of density less than the density of ball. The motion of the ball is
View SolutionA ball is dropped on a horizontal surface from height h. If it rebounds upto height h2 after first collision then coefficient of restitution between ball and surface is
View Solution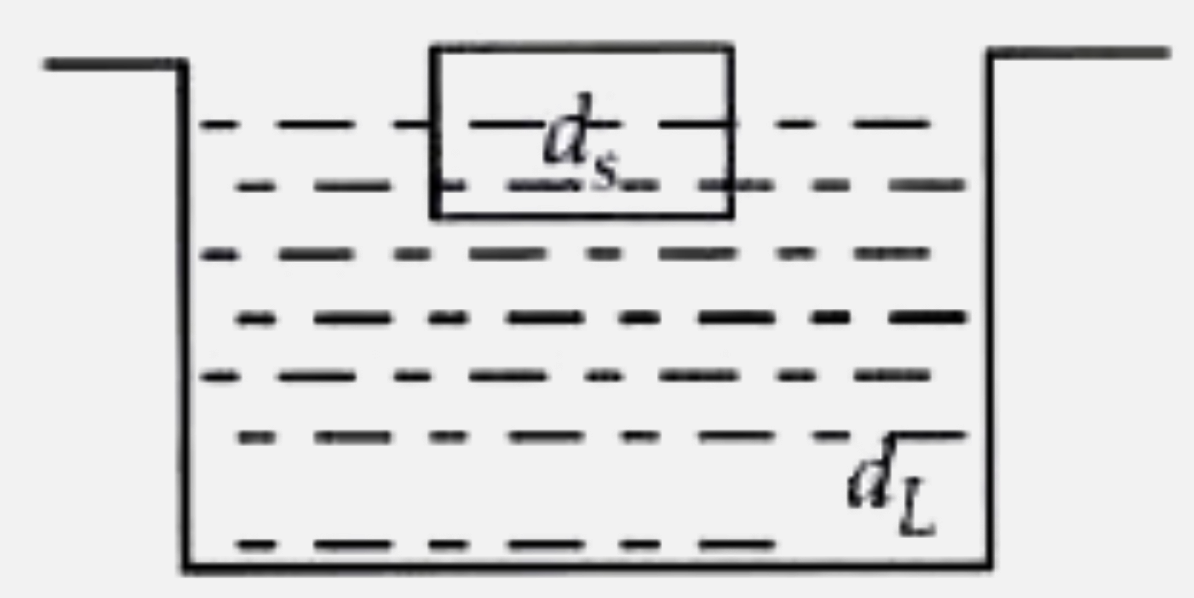
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the relation between dS and dL in the above case?View SolutionA wooden ball of density D is immersed in water of density d to a depth h//2 below the surface of water and then relased. To what height will the ball jump out of water ?
View SolutionA ball of mass m is dropped onto a floor from a certain height. The collision is perfectly elastic and the ball rebounds to the same height and again falls. Find the average force exerted by the ball on the floor during a long time interval.
View SolutionA ball rises to the surface of a liquid with constant velocity. The density of the liquid is four time the density of the material of the ball. The frictional force of the liquid on the rising ball is greater than the weight of the ball by a factor of
View SolutionA ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
View Solution

