A ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
h
h/2
2h
3h
The correct Answer is:C
To solve the problem of how high a ball of mass m and density ρ will jump above the surface of a liquid of density 3ρ when released from a depth h, we can follow these steps:
1. Identify the Forces Acting on the Ball:
- The ball experiences two main forces when submerged in the liquid:
- Weight (W): The weight of the ball is given by:
W=ρVg
where V is the volume of the ball and g is the acceleration due to gravity.
- Buoyant Force (F_b): The buoyant force acting on the ball is given by Archimedes' principle:
Fb=3ρVg
since the density of the liquid is 3ρ.
2. Calculate the Net Upward Force:
- The net upward force Fnet acting on the ball when it is released can be calculated as:
Fnet=Fb−W=3ρVg−ρVg=2ρVg
3. Determine the Acceleration of the Ball:
- Using Newton's second law, the acceleration a of the ball can be found:
a=Fnetm=2ρVgρV=2g
- Here, the mass m of the ball is ρV, which cancels out.
4. Calculate the Velocity of the Ball at the Surface:
- Using the kinematic equation v2=u2+2as, where:
- u=0 (initial velocity),
- a=2g (acceleration),
- s=h (distance submerged),
- We find:
v2=0+2⋅2g⋅h=4gh
- Therefore, the velocity v of the ball when it reaches the surface of the liquid is:
v=2√gh
5. Determine the Height the Ball Will Rise Above the Surface:
- Once the ball reaches the surface, it will continue to move upward until its velocity becomes zero. We again use the kinematic equation:
0=v2−2gs
where s is the height above the surface of the liquid that we want to find. Rearranging gives:
s=v22g=(2√gh)22g=4gh2g=2h
Thus, the height to which the ball will jump above the surface of the liquid is 2h.
Final Answer:
The ball will jump to a height of 2h above the surface of the liquid.
- The ball experiences two main forces when submerged in the liquid:
- Weight (W): The weight of the ball is given by:
W=ρVg
where V is the volume of the ball and g is the acceleration due to gravity.
- Buoyant Force (F_b): The buoyant force acting on the ball is given by Archimedes' principle:
Fb=3ρVg
since the density of the liquid is 3ρ.
- The net upward force Fnet acting on the ball when it is released can be calculated as:
Fnet=Fb−W=3ρVg−ρVg=2ρVg
- Using Newton's second law, the acceleration a of the ball can be found:
a=Fnetm=2ρVgρV=2g
- Here, the mass m of the ball is ρV, which cancels out.
- Using the kinematic equation v2=u2+2as, where:
- u=0 (initial velocity),
- a=2g (acceleration),
- s=h (distance submerged),
- We find:
v2=0+2⋅2g⋅h=4gh
- Therefore, the velocity v of the ball when it reaches the surface of the liquid is:
v=2√gh
- Once the ball reaches the surface, it will continue to move upward until its velocity becomes zero. We again use the kinematic equation:
0=v2−2gs
where s is the height above the surface of the liquid that we want to find. Rearranging gives:
s=v22g=(2√gh)22g=4gh2g=2h
The ball will jump to a height of 2h above the surface of the liquid.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A small ball of density ρ is immersed in a liquid of density σ(>ρ) to a depth h and released. The height above the surface of water up to which the ball will jump is
View SolutionA wooden ball of density D is immersed in water of density d to a depth h//2 below the surface of water and then relased. To what height will the ball jump out of water ?
View Solution
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
A ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
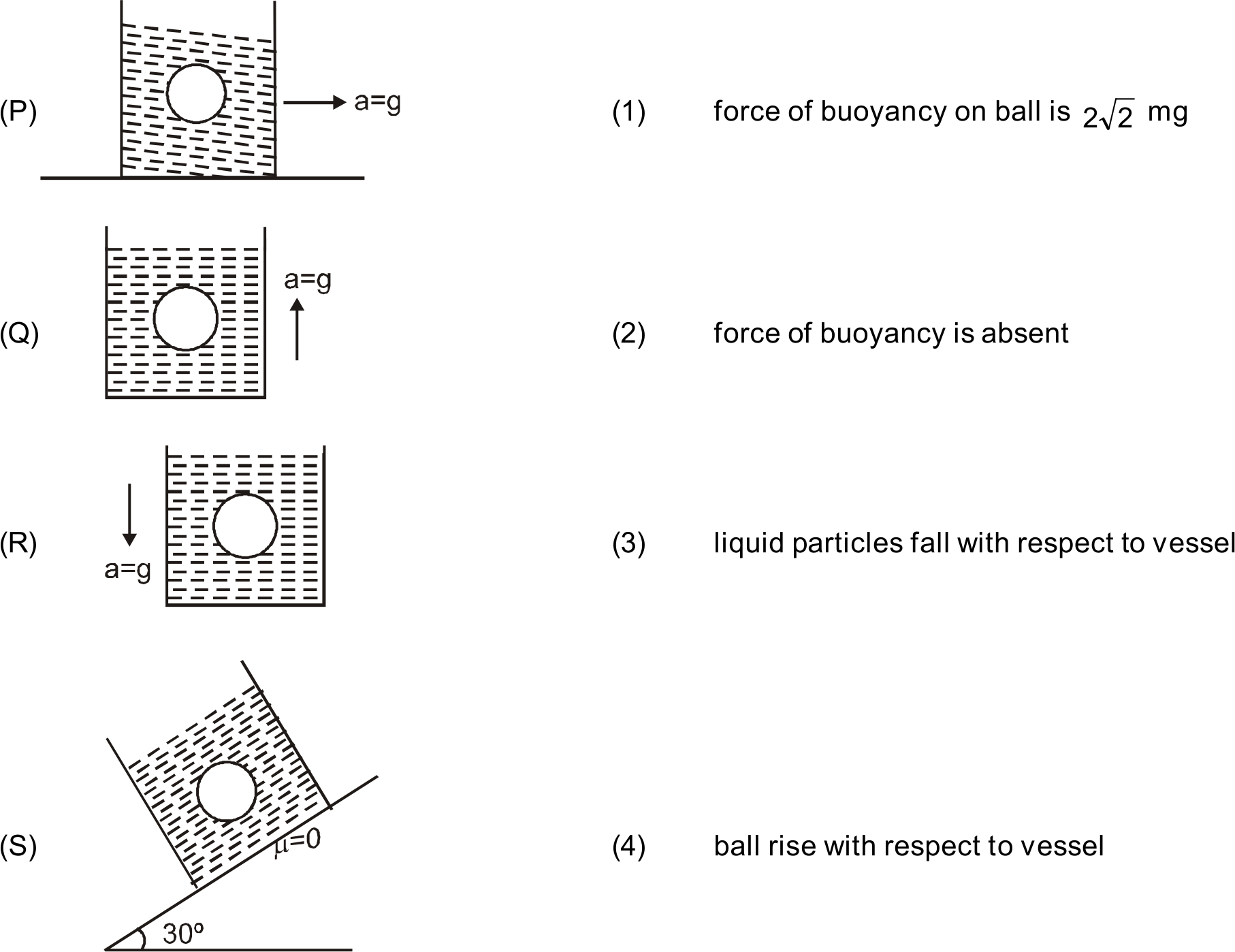
View SolutionA ball of mass m and density ρ2 is completely immersed in a liquid of density ρ, contained in an accelerating vessel as shown.Select the correct answer using the codes given below the columns.
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionA cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
View SolutionA beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
View SolutionA ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.

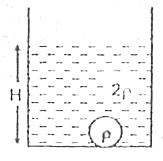
View SolutionA small ball of density ρ is placed from the bottom of a tank in which a non viscous liquid of density 2ρ is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )
View Solution
