Is their any relationship between wave speed and the maximum partcle speed for a wave travelling on a string? If so, what is it?
The correct Answer is:A
To find the relationship between wave speed and the maximum particle speed for a wave traveling on a string, we can follow these steps:
Step 1: Understand the Definitions
- Maximum Particle Speed (V_max): This is the maximum speed of the particles of the medium (in this case, the string) as the wave passes through.
- Wave Speed (v): This is the speed at which the wave travels along the string.
Step 2: Write the Expression for Maximum Particle Speed
The maximum particle speed can be expressed as:
Vmax=ω⋅A
where:
- ω is the angular frequency of the wave,
- A is the amplitude of the wave.
Step 3: Write the Expression for Wave Speed
The wave speed can be expressed as:
v=ωk
where:
- k is the wave number.
Step 4: Relate Angular Frequency to Wave Speed
From the first equation, we can express ω as:
ω=VmaxA
From the second equation, we can express ω as:
ω=v⋅k
Step 5: Equate the Two Expressions for Angular Frequency
Now, we can set the two expressions for ω equal to each other:
VmaxA=v⋅k
Step 6: Solve for Maximum Particle Speed
To find Vmax, we rearrange the equation:
Vmax=v⋅A⋅k
Conclusion
Thus, the relationship between wave speed and maximum particle speed is given by:
Vmax=v⋅A⋅k
- Maximum Particle Speed (V_max): This is the maximum speed of the particles of the medium (in this case, the string) as the wave passes through.
- Wave Speed (v): This is the speed at which the wave travels along the string.
The maximum particle speed can be expressed as:
Vmax=ω⋅A
where:
- ω is the angular frequency of the wave,
- A is the amplitude of the wave.
The wave speed can be expressed as:
v=ωk
where:
- k is the wave number.
From the first equation, we can express ω as:
ω=VmaxA
ω=v⋅k
Now, we can set the two expressions for ω equal to each other:
VmaxA=v⋅k
To find Vmax, we rearrange the equation:
Vmax=v⋅A⋅k
Thus, the relationship between wave speed and maximum particle speed is given by:
Vmax=v⋅A⋅k
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 Single Correct5videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 More Than One Correct6videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 1 Objective6videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
Knowledge Check
- Question 1 - Select One
The speed of transverse wave on a stretched string is
Adirectly proportional to the tension in the stringBdirectly proportional to the square root of the tensionCinversely proportional to liveDinversely proportional to sqyare of tension
State two factors on which the speed of a wave travelling in a medium depends.
View SolutionMark out the correct statement (S) e.r.t. wave speed and particle velocity for a transverse travelling mechanical wave on a string.
View SolutionState the factors on which the speed of a wave travelling along a stretched ideal string depends.
View SolutionA string of length 2L, obeying hooke's law, is stretched so that its extension is L. the speed of the transverse wave travelling on the string is v. If the string is further stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionA string of length 2L, obeying Hooke's Law, is stretched so that its extension is L. The speed of the tranverse wave travelling on the string is v. if the string is futher stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionA uniform circular hoop of string is rotating clockwise in the absence of gravity. The tangential speed is v0. Find the speed of the wave travelling on this string.
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
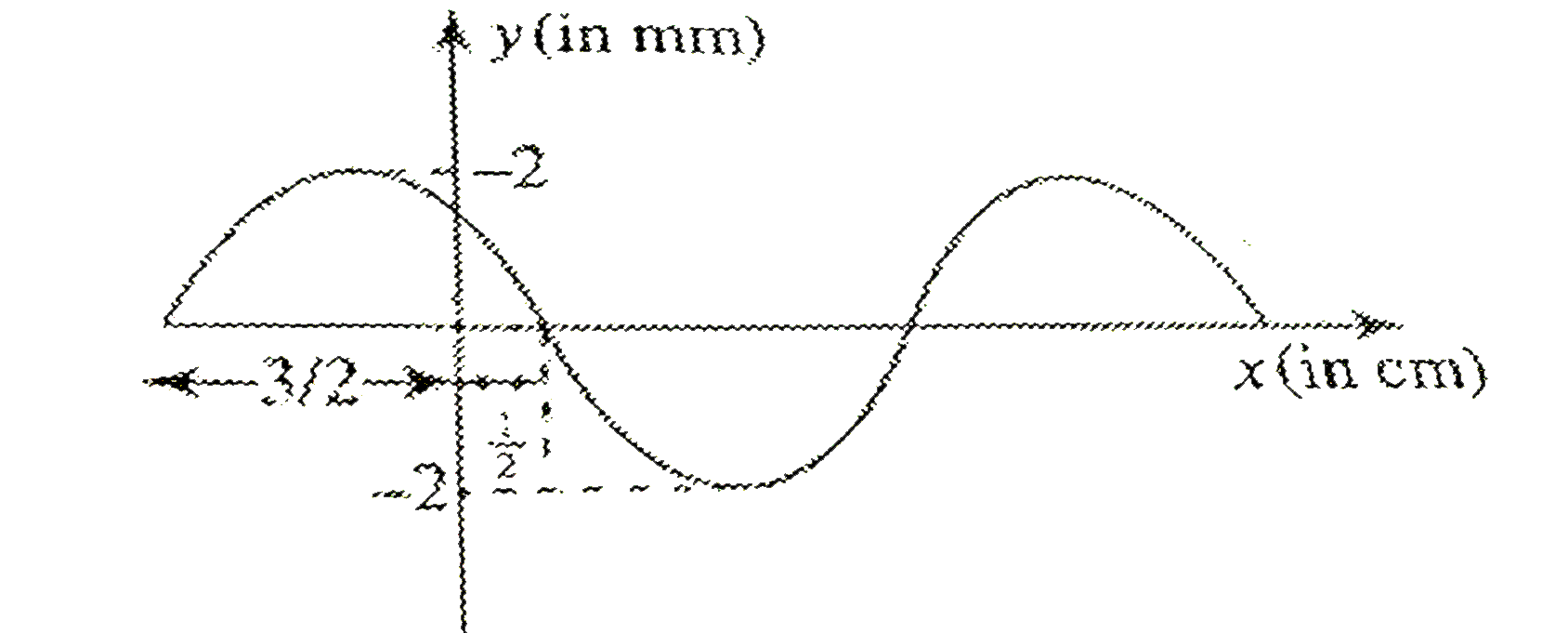
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.View Solution

