A loop of rope is whirled at a high angular velocity, so that it becomes a taut circle of radius. A kink develops in the whirling rope. 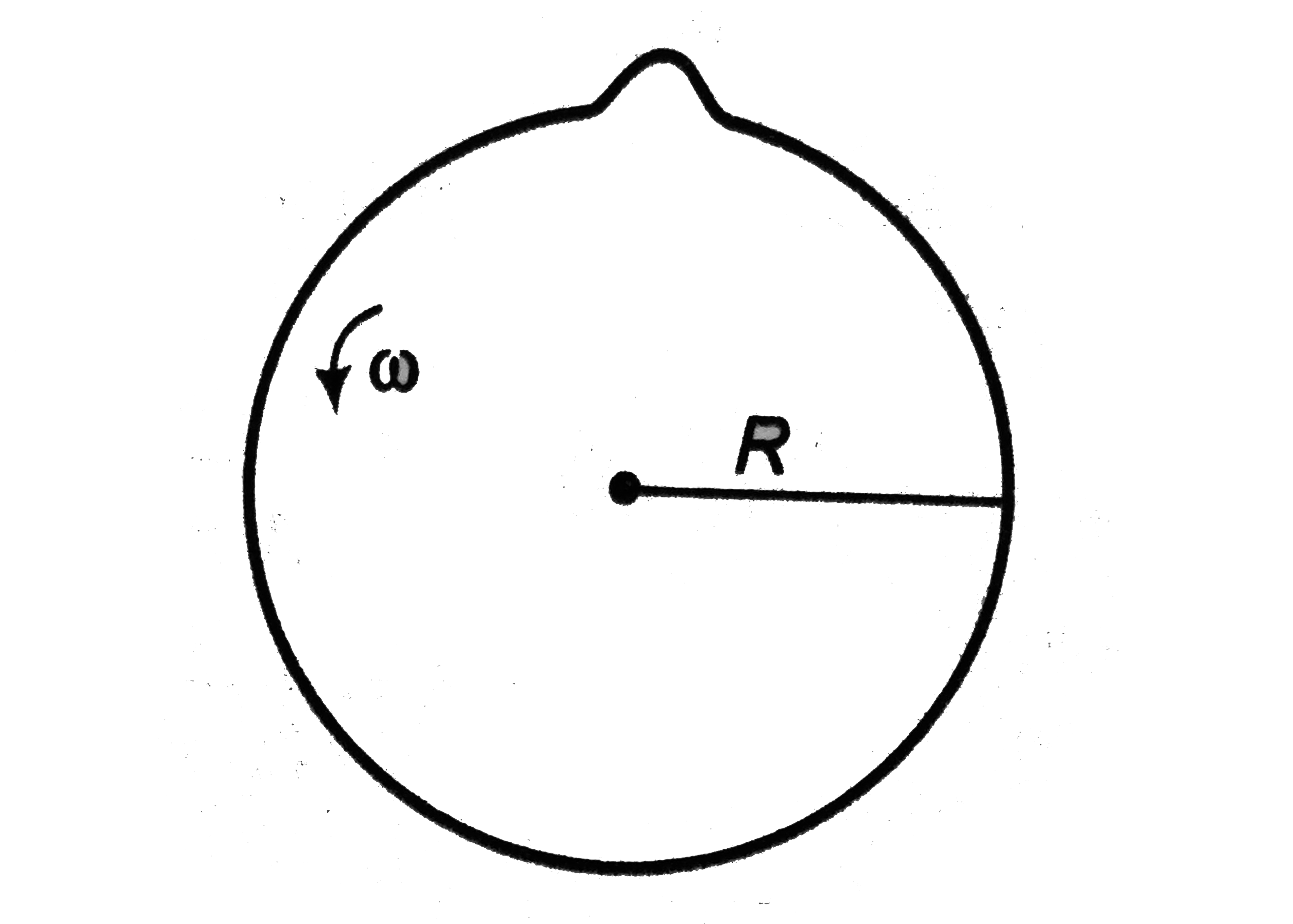
(a) Show that the speed of the kink in the rope is .
(b) Under what conditions does the kink remains stationary relative to an observer on the ground?
The correct Answer is:A, B, C, D
(a) components are cancelled. components provided the necessary centriprtal force to .

For small angles
Solving thr equation, we get
Topper's Solved these Questions
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Level 2 Single Correct
Explore 5 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Level 2 More Than One Correct
Explore 6 Videos
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Level 1 Objective
Explore 6 Videos
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Medical enrances gallery
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
Similar Questions
A loop of rope is whirled at a high angular velocityω, so that it becomes a taut circle of radius r.
(a) Find the tension in the rope it the linear mass density of the rope is μ
(b) A kink develops in the whirling rope. Under what condition does the kink remain stationary relative to an observer on the ground?
View SolutionA hoop of mass m is projected on a floor with linear velocity v0 and reverse spin ω0. The coefficient of friction between the hoop and the ground is μ.
a. Under what condition will the hoop return back?
b. How far will it go?
c. How long will it continue to slip when its centre of mass becomes stationary?
d. What is the velocity of return?
View SolutionA string is wrapped several times on a cylinder of mass M and radius R. the cylinder is pivoted about its adxis of block symmetry. A block of mass m tied to the string rest on a support positioned so that the string has no slack. The block is carefully lifted vertically a distance h, and the support is removed as shown figure.
a. just before the string becomes taut evalute the angular velocity ω0 of the cylinder ,the speed v0 of the falling body, m and the kinetic energy K0 of the system.
b. Evaluate the corresponding quanitities ω1,v1 and K1 for the instant just after the string becomes taut.
c. Why is K1 less than K0? Where does the energy go?
d. If M=m, what fraction of the kinetic energy is lost when the string becomes taut?
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. If the sphere in previous question has mass of 1×10−5kg what is its terminal velocity when falling through water? (η=1×10−3Pa−s)
A. 1.3m/s
B. 3.4m/s
C. 5.2m/s
D. 6.5m/s
View Solution