Assertion: A wire is stretched and then fixed at two ends. It oscillates in its second overtone mode. There are total four nodes and three antinodes.
Reason: In second overtone mode, length of wire should be l=3λ2, where λ is wavelength.
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:B
To solve the problem, we need to analyze both the assertion and the reason provided in the question.
1. Understanding the Assertion:
- The assertion states that a wire fixed at both ends oscillates in its second overtone mode, resulting in four nodes and three antinodes.
- In a standing wave pattern, nodes are points where the amplitude is zero, and antinodes are points where the amplitude is maximum.
2. Identifying Nodes and Antinodes:
- In the second overtone mode (which is the third harmonic), the pattern consists of:
- Nodes: 4 (including the ends)
- Antinodes: 3 (the points between the nodes)
- This matches the assertion, confirming that it is true.
3. Understanding the Reason:
- The reason states that in the second overtone mode, the length of the wire L is given by the formula L=3λ2, where λ is the wavelength.
- To verify this, we need to understand the relationship between the length of the wire and the wavelength in the context of standing waves.
4. Calculating the Length of the Wire:
- In the second overtone mode, the pattern consists of 3 antinodes and 4 nodes.
- The distance between two consecutive nodes is λ2 (half a wavelength).
- Therefore, the length of the wire can be calculated as:
- The distance from the first node to the last node (which includes 3 segments of λ2):
- L=3×λ2=3λ2
- This confirms that the reason is also true.
5. Conclusion:
- Both the assertion and the reason are true.
- However, the reason does not explain the assertion directly; it merely states a property of the second overtone mode.
Final Answer:
- Assertion: True
- Reason: True
- Conclusion: Both statements are true, but the reason does not directly relate to the assertion.
- The assertion states that a wire fixed at both ends oscillates in its second overtone mode, resulting in four nodes and three antinodes.
- In a standing wave pattern, nodes are points where the amplitude is zero, and antinodes are points where the amplitude is maximum.
- In the second overtone mode (which is the third harmonic), the pattern consists of:
- Nodes: 4 (including the ends)
- Antinodes: 3 (the points between the nodes)
- This matches the assertion, confirming that it is true.
- The reason states that in the second overtone mode, the length of the wire L is given by the formula L=3λ2, where λ is the wavelength.
- To verify this, we need to understand the relationship between the length of the wire and the wavelength in the context of standing waves.
- In the second overtone mode, the pattern consists of 3 antinodes and 4 nodes.
- The distance between two consecutive nodes is λ2 (half a wavelength).
- Therefore, the length of the wire can be calculated as:
- The distance from the first node to the last node (which includes 3 segments of λ2):
- L=3×λ2=3λ2
- This confirms that the reason is also true.
- Both the assertion and the reason are true.
- However, the reason does not explain the assertion directly; it merely states a property of the second overtone mode.
- Assertion: True
- Reason: True
- Conclusion: Both statements are true, but the reason does not directly relate to the assertion.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Objective11videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Objective Questions1videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.43videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
Similar Questions
A wire is stretched and fixed at two ends. Transverse stationary waves are formed in it. It oscillates in its third overtone mode. The equation of stationary wave is
y=Asinkxcosωt
Choose the correct options.View SolutionAssertion: If we see the oscillations of a stretched wire at higher overtone mode, frequency of oscillation increases but wavelength decreases.
Reason: From v=fλ,λ∝1f as v = constant.View SolutionA stretched wire is oscillating in third overtone mode. Equation of transverse stationary wave produced in this wire is
y=Asin(6πx)sin(20πt)
Here, x is in metres. Find the length of the wire.View SolutionLength of a stretched wire is 2m. It is oscillating in its fourth overtone mode. Maximum amplitude of oscillations is 2mm. Find amplitude of oscillation at a distance of 0.2m from one fixed end.
View SolutionTransverse waves are produced in a stretched wire. Both ends of the string are fixed. Let us compare between second overtone mode (in numerator) and fifth harmonic, mode (in denominator).
match the following column-I with column-II
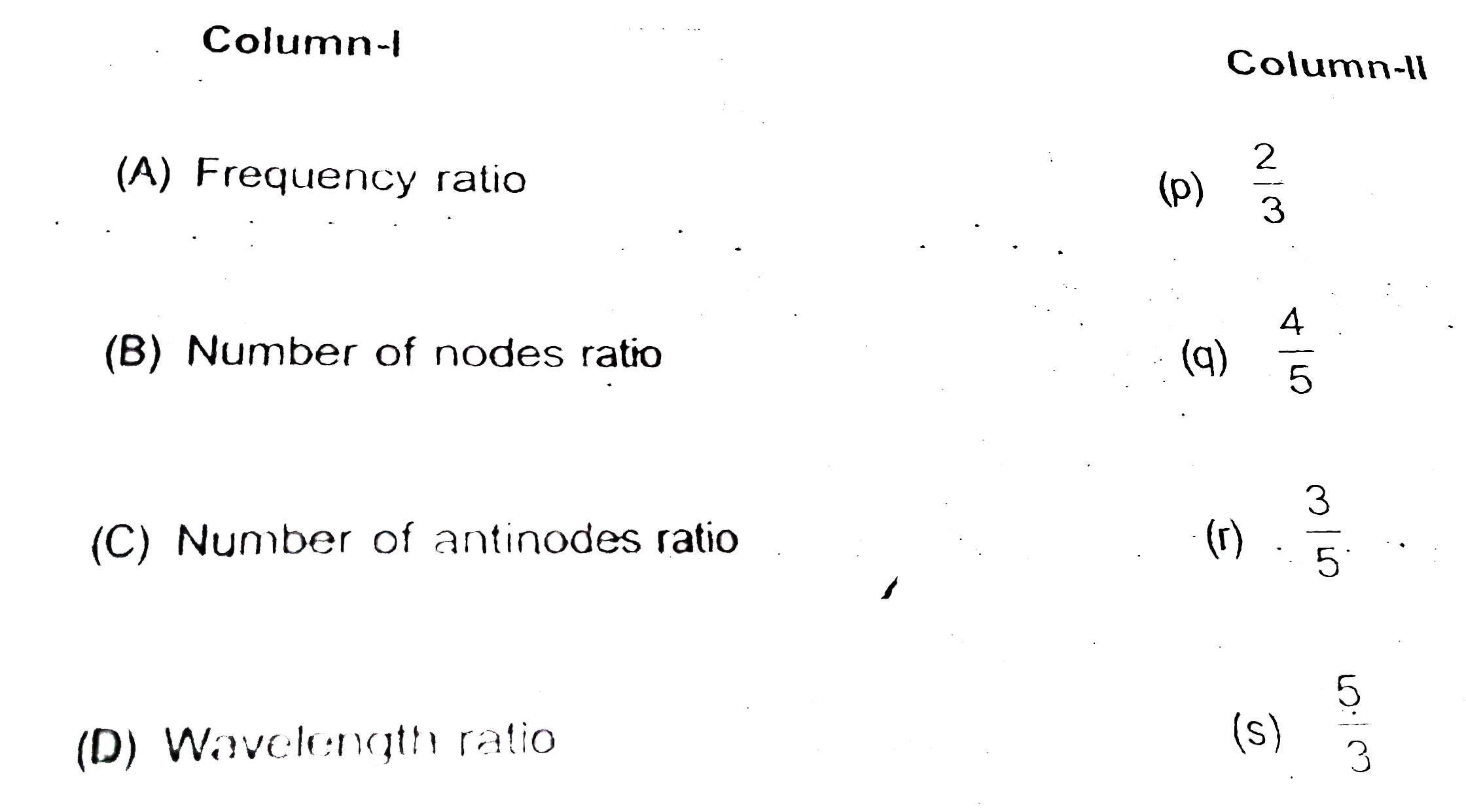 View Solution
View SolutionA wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire.
 View Solution
View SolutionA wire of length 40 cm which has a mass of 4 gms oscillates in its second harmonic and sets the air column in the tube to vibrations in its fundamental mode as shown in figure. Assuming speed of sound in air as 340 m/s, find the tension in the wire.
 View Solution
View SolutionA string of linear mass density 5.0×10−3 kg//m is stretched under a tension of 65 N between two rigid supports 60 cm apart.
(a) If the string is vibrating in its second overtone so that the amplitude at one of its antinodes is 0.25 cm, what are the maximum transverse speed and acceleration of the string at antinodes?
(b) What are these quantities at a distance 5.0 cm from an node?View SolutionTwo different stretched wires have same tension and mass per unit length. Fifth overtone frequency of the first wire is equal to second harmonic frequency of the second wire. Find the ratio of their lengths.
View SolutionA tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .View Solution

