In a standing wave, node is a point of
maximum strain
maximum pressure
maximum density
All of these
The correct Answer is:D
To solve the question "In a standing wave, node is a point of", we need to analyze the characteristics of nodes in standing waves. Here’s a step-by-step solution:
Step 1: Understand the Concept of Standing Waves
A standing wave is formed by the superposition of two waves traveling in opposite directions. It consists of nodes and antinodes. Nodes are points where there is no displacement, while antinodes are points of maximum displacement.
Hint: Recall that nodes are points of no movement in a standing wave.
Step 2: Define a Node
At a node, the displacement of the medium is always zero. This means that the particles at the node do not oscillate; they remain stationary.
Hint: Think about what happens to particles at a node in terms of their motion.
Step 3: Analyze Pressure Variation
In a standing wave, the pressure variation is related to the displacement. At a node (where displacement is zero), the pressure variation is at a maximum. This is because when particles are at rest, they are compressed, leading to higher pressure.
Hint: Consider the relationship between displacement and pressure in wave mechanics.
Step 4: Consider Density
Density is also affected by pressure. According to the principles of fluid dynamics, when pressure increases, the density of the medium also increases. Therefore, at a node, where pressure is maximum, the density will also be maximum.
Hint: Reflect on how pressure and density are related in a compressible medium.
Step 5: Strain in the Medium
Strain is a measure of deformation representing the displacement between particles in a material body. At a node, since the particles are compressed and not moving, the strain is also at its maximum.
Hint: Think about how strain relates to the movement of particles in a wave.
Conclusion
Thus, at a node in a standing wave, we find that:
- The displacement is zero.
- The pressure is at a maximum.
- The density is at a maximum.
- The strain is also at a maximum.
Therefore, the correct answer to the question is that a node is a point of maximum strain, maximum pressure, and maximum density.
Final Answer: All of the above (maximum strain, maximum pressure, maximum density).
A standing wave is formed by the superposition of two waves traveling in opposite directions. It consists of nodes and antinodes. Nodes are points where there is no displacement, while antinodes are points of maximum displacement.
At a node, the displacement of the medium is always zero. This means that the particles at the node do not oscillate; they remain stationary.
In a standing wave, the pressure variation is related to the displacement. At a node (where displacement is zero), the pressure variation is at a maximum. This is because when particles are at rest, they are compressed, leading to higher pressure.
Density is also affected by pressure. According to the principles of fluid dynamics, when pressure increases, the density of the medium also increases. Therefore, at a node, where pressure is maximum, the density will also be maximum.
Strain is a measure of deformation representing the displacement between particles in a material body. At a node, since the particles are compressed and not moving, the strain is also at its maximum.
Thus, at a node in a standing wave, we find that:
- The displacement is zero.
- The pressure is at a maximum.
- The density is at a maximum.
- The strain is also at a maximum.
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Subjective
24 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Subjective Questions
6 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Objective
11 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
Similar Questions
In a standing wave 4 nodes and 3 antinodes are formed between two fixed end of string of length 6 m.Then the wave length of the standing wave is
View SolutionAssertion: In a standing wave x=0 is a node. Then, total mechanical energy lying between x=0 and x=(λ8) is not equal to the energy lying between x=λ8 and x=λ4.
Reason: In standing waves different particles oscillate with different amplitudes.
View Solution
Knowledge Check
In a stationary longitudinal wave, nodes are points of
Aminimum displacement and minimum pressure change.Bminimum displacement and maximum pressure changeCmaximum displacement and maximum pressure changeDmaximum displacement and minimum pressure change.
Statement I : In a standing wave on a string , the spacing between nodes is Δx. If the tension in string is increased wave same as before , then the separation between nearest nodes will be increased.
Statement II : Spacing between nodes ( consecutive) in the standing wave is equal to half of the wavelength of component waves.
View SolutionIn a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is328ms−1 what is the frequency of the source ?
View SolutionIn a standing wave particles at the positions A and B, have a phase difference of
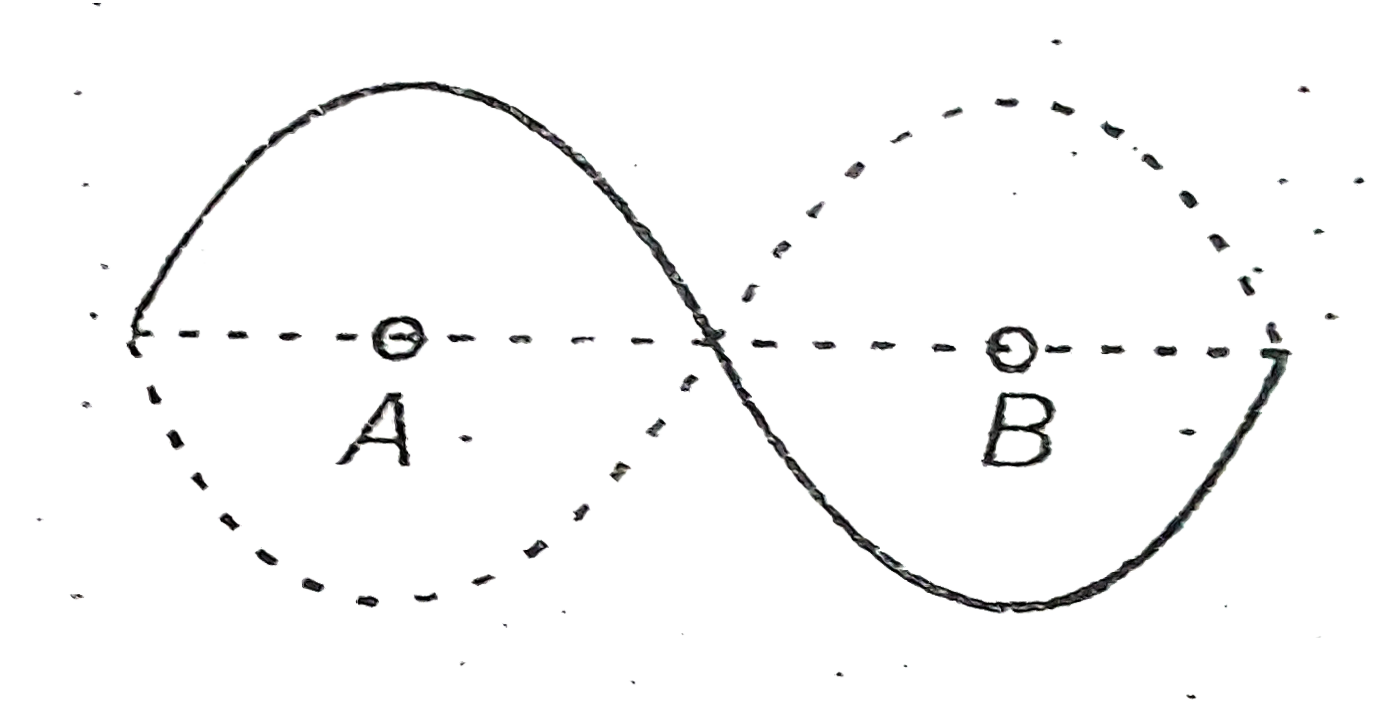
View SolutionLet the two waves y1=Asin(kx−ωt) and y2=Asin(kx+ωt) from a standing wave on a string . Now if an additional phase difference of ϕ is created between two waves , then
View SolutionSpacing between two successive nodes in a standing wave on a string is x. If frequency of the standing wave is kept unchanged but tension in the string is doubled, then new sapcing between successive nodes will become:
View SolutionWhich of the following travelling wave will produce standing wave , with nodes at x=0, when superimosed on y=Asin(ωt−kx)
View SolutionWhich of the following travelling wave will produce standing wave , with nodes at x=0, when superimosed on y=Asin(ωt−kx)
View Solution
