A string tied between x=0andx=l vibrates in fundamental mode. The amplitude A, tension T and mass per unit length μ is given. Find the total energy of the string.

The correct Answer is:A, B, D
l=λ2
or λ=2l,k=2πλ=πl

The amplitude at a distance x from x = 0 is given by
A=asinkx
Total mechanical energy at x of length dx is
dE=12(dm)A2ω2
=12(μdx)(asinkx)2(2πf)2
or dE=2π2μf2a2sin2kxdx .........(i)
Here, f=(v2λ2)=(Tμ)(4l2)andk=πl
Substituting these values in Eq. (i) and integrating it from x = 0 to x = l , we get total energy of string.
E=π2a2T4l .
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Comprehension Based3videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
Similar Questions
A string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).
 View Solution
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA uniform string is clamped at x=0 and x = L and is vibrating in its fundamental mode. Mass per unit length of the string is μ, tension in it is T and the maximum displacement of its midpoint is A. Find the total energy stored in the string. Assume to be small so that changes in tension and length of the string can be ignored
View SolutionA sonometer wire of length l vibrates in fundamental mode when excited by a tunning fork of frequency 416 Hz. If the length is double keeping other things same the string will
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
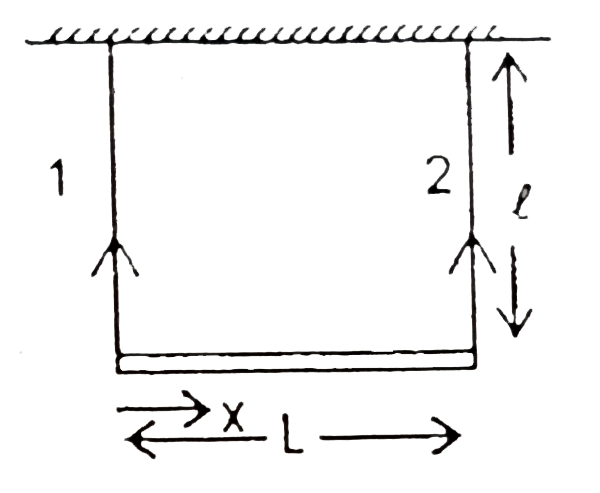 View Solution
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View SolutionA middle C string on a piano has a fundamental frequency of 262Hz, and the A note has fundamental frequency of 440Hz. (a) Calculate the frequencies of the next two harmonics of the C string. (b) If the strings for the A and C notes are assumed to have the same mass per unit length and the same length, determine the ratio of tension in the two strings.
View SolutionCalculate the time taken for a disturbance to pass through a string of length I and of mass per unit length m when the tension in the string is mI2gN.
View SolutionDerive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
View Solution

