A fighter plane moving in a vertical loop with constant speed of radius R . The center of the loop is as a height h directly overhead of an observer standing on the ground. The observer receives maximum frequency of the sound produced by the plane when it is nearest to him . Find the speed of the plane. Velocity of sound in air is υ .
The correct Answer is:A, B
To find the speed of the fighter plane moving in a vertical loop with radius R, we can use the concept of the Doppler effect and the geometry of the situation. Here’s a step-by-step solution:
Step 1: Understand the Geometry
The observer is standing on the ground at a distance h directly below the center of the loop. When the plane is at its nearest point to the observer, it is directly above the observer. The distance from the center of the loop to the observer is h, and the radius of the loop is R.
Step 2: Identify the Relevant Distances
When the plane is at the nearest point, the distance from the plane to the observer (let's call this distance SO) can be calculated using the Pythagorean theorem:
SO=√h2+R2
Step 3: Use the Doppler Effect
The observer receives the maximum frequency when the plane is moving directly towards him. According to the Doppler effect, the frequency heard by the observer is maximized when the source (the plane) is moving towards the observer. The time taken for the sound to travel from the plane to the observer must equal the time taken for the plane to move a small distance towards the observer.
Step 4: Set Up the Time Equations
Let vs be the speed of the plane and v be the speed of sound in air. The time taken for sound to travel from the plane to the observer is:
t=SOv
The time taken for the plane to move a distance Δs towards the observer is:
t=Δsvs
Step 5: Relate the Distances and Speeds
For maximum frequency, these two times must be equal:
SOv=Δsvs
Rearranging gives:
vs=Δs⋅vSO
Step 6: Determine Δs
The distance Δs is the arc length the plane travels in a very small time interval. For small angles, this can be approximated as:
Δs=R⋅θ
where θ is the angle subtended at the center of the loop.
Step 7: Substitute Back
Substituting Δs into the equation gives:
vs=R⋅θ⋅vSO
Now, substituting SO=√h2+R2:
vs=R⋅θ⋅v√h2+R2
Step 8: Find θ
Using trigonometry, we find θ using the cosine function:
cosθ=Rh⟹θ=cos−1(Rh)
Step 9: Final Expression
Substituting θ back into the equation gives:
vs=R⋅cos−1(Rh)⋅v√h2+R2
Conclusion
The speed of the plane vs can be expressed as:
vs=R⋅v⋅cos−1(Rh)√h2+R2
The observer is standing on the ground at a distance h directly below the center of the loop. When the plane is at its nearest point to the observer, it is directly above the observer. The distance from the center of the loop to the observer is h, and the radius of the loop is R.
When the plane is at the nearest point, the distance from the plane to the observer (let's call this distance SO) can be calculated using the Pythagorean theorem:
SO=√h2+R2
The observer receives the maximum frequency when the plane is moving directly towards him. According to the Doppler effect, the frequency heard by the observer is maximized when the source (the plane) is moving towards the observer. The time taken for the sound to travel from the plane to the observer must equal the time taken for the plane to move a small distance towards the observer.
Let vs be the speed of the plane and v be the speed of sound in air. The time taken for sound to travel from the plane to the observer is:
t=SOv
The time taken for the plane to move a distance Δs towards the observer is:
t=Δsvs
For maximum frequency, these two times must be equal:
SOv=Δsvs
Rearranging gives:
vs=Δs⋅vSO
The distance Δs is the arc length the plane travels in a very small time interval. For small angles, this can be approximated as:
Δs=R⋅θ
where θ is the angle subtended at the center of the loop.
Substituting Δs into the equation gives:
vs=R⋅θ⋅vSO
Now, substituting SO=√h2+R2:
vs=R⋅θ⋅v√h2+R2
Using trigonometry, we find θ using the cosine function:
cosθ=Rh⟹θ=cos−1(Rh)
Substituting θ back into the equation gives:
vs=R⋅cos−1(Rh)⋅v√h2+R2
The speed of the plane vs can be expressed as:
vs=R⋅v⋅cos−1(Rh)√h2+R2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 1 Assertion And Reason10videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 1 Objective34videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - TYPE 5.2videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective8videos
SUPERPOSITION OF WAVES
Similar Questions
An observer standing on a railway crossing receives frequencies 2.2 kHz and 1.8 kHz when the tran approaches and recedes from the observer. Find the velocity of the train (speed of sound in air is 300 m/s).
View Solution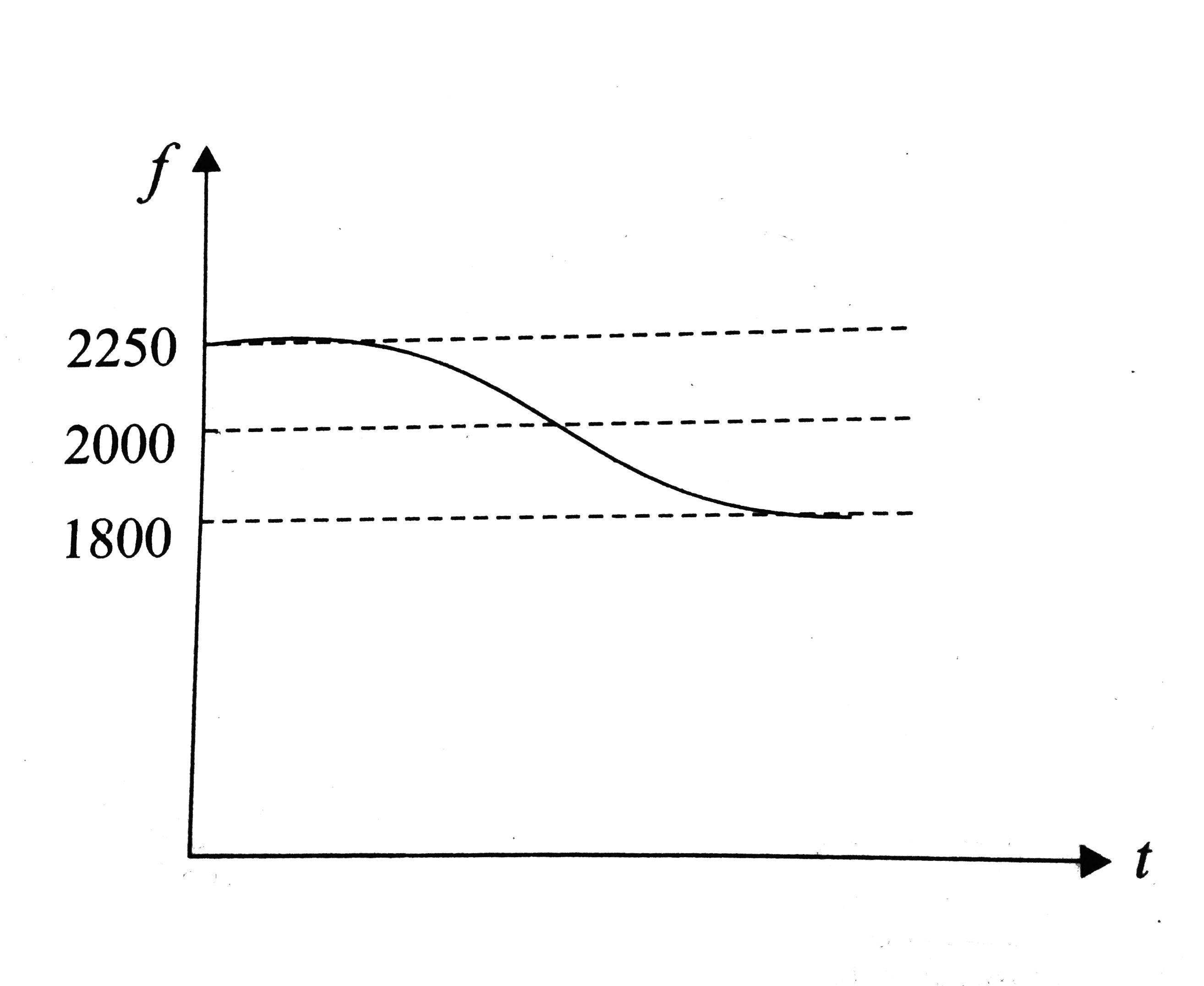
A statinary observer receives a sound of frequency 2000 Hz. The variation of apparent frequency and time is shown. Find the speed of source, if velocity of sound is 300msView SolutionThe ratio of the apparent frequencies of a car when approaching and receding a stationary observer is 11:9 What is the speed of the car, if the velocity of sound in air is 330 m/s?
View SolutionA siren emitting a sound of frequency 800 Hz moves away from an observer towards a cliff at a speed of 15ms−1. Then the frequency of sound that the observer hears in the echo reflected from the cliff is (Take velocity of sound in air =330ms−1)
View SolutionA block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
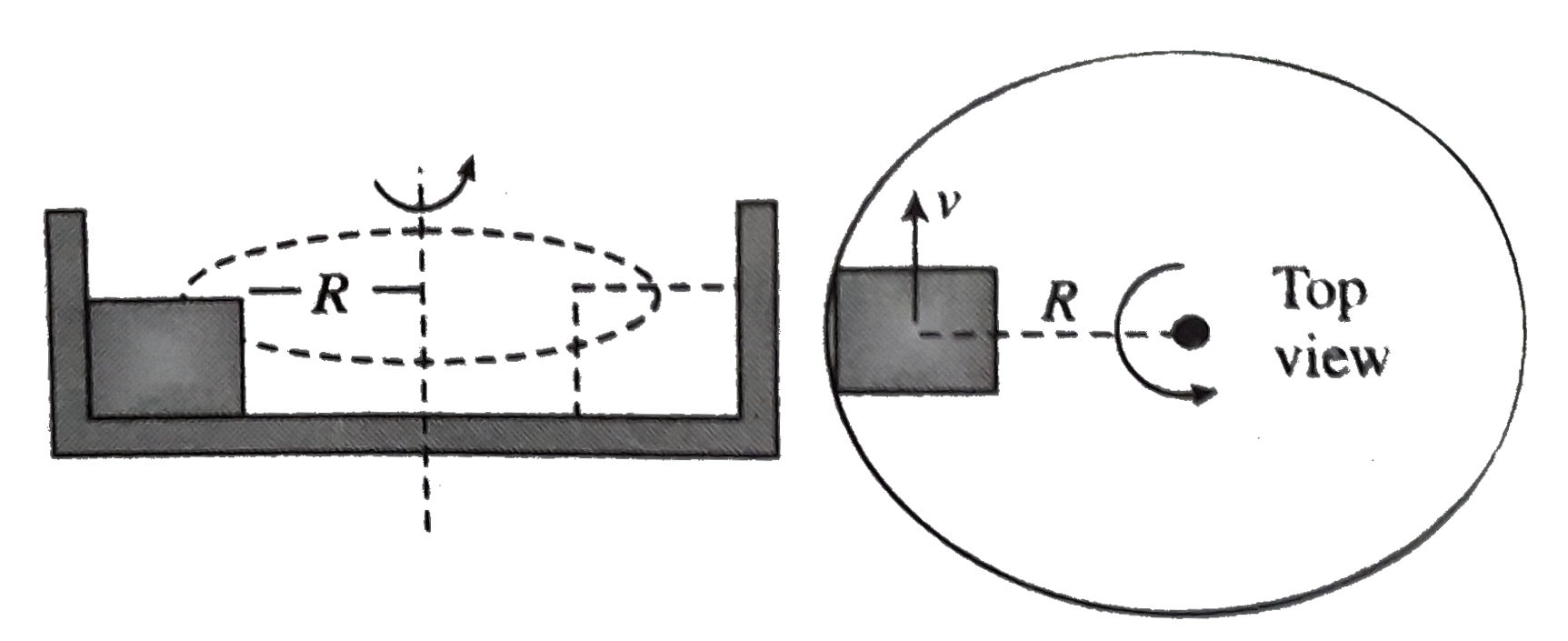 View Solution
View SolutionTwo tuning forks with natural frequencies 340HZ each move relative to a stationary observer . One forks moves away from the oberver while the other moves towards him at the same speed . The observer hears beats of frequency 3HZ . Find the speed the of the tuning fork (velocity of sound in air is 340m/s) .
View SolutionA van is moving with a speed of 3ms−1 towards a large wall. A person standing on the line of motion of the van observes the van to be moving away from him. The horm of the van is now blown. The frequency of the sound produced by the horn is 600 Hz. what is
(i) The frequency of sound heard by the person for the sound produced directly by the horn?
(ii) The freuquency of sound reflected by the wall.
(iii) The baat frequency heard by the driver. the speed of sound in air is 330ms−1?View SolutionSource and observer start moving simulatneously along x and y-axis respectively. The speed of source is twice the speed of observer V0. If the ratio of observer frequency to the frequency of the source is 0.75, find the velocity of sound.
View SolutionSource and observer start moving simulatneously along x and y-axis respectively. The speed of source is twice the speed of observer V0. If the ratio of observer frequency to the frequency of the source is 0.75, find the velocity of sound.
View SolutionA train of length l is moving with a constant speed υ along a circular track of radius R. The engine of the train emits a sound of frequency f. Find the frequency heard by a guard at the rear end of the train.
View Solution

