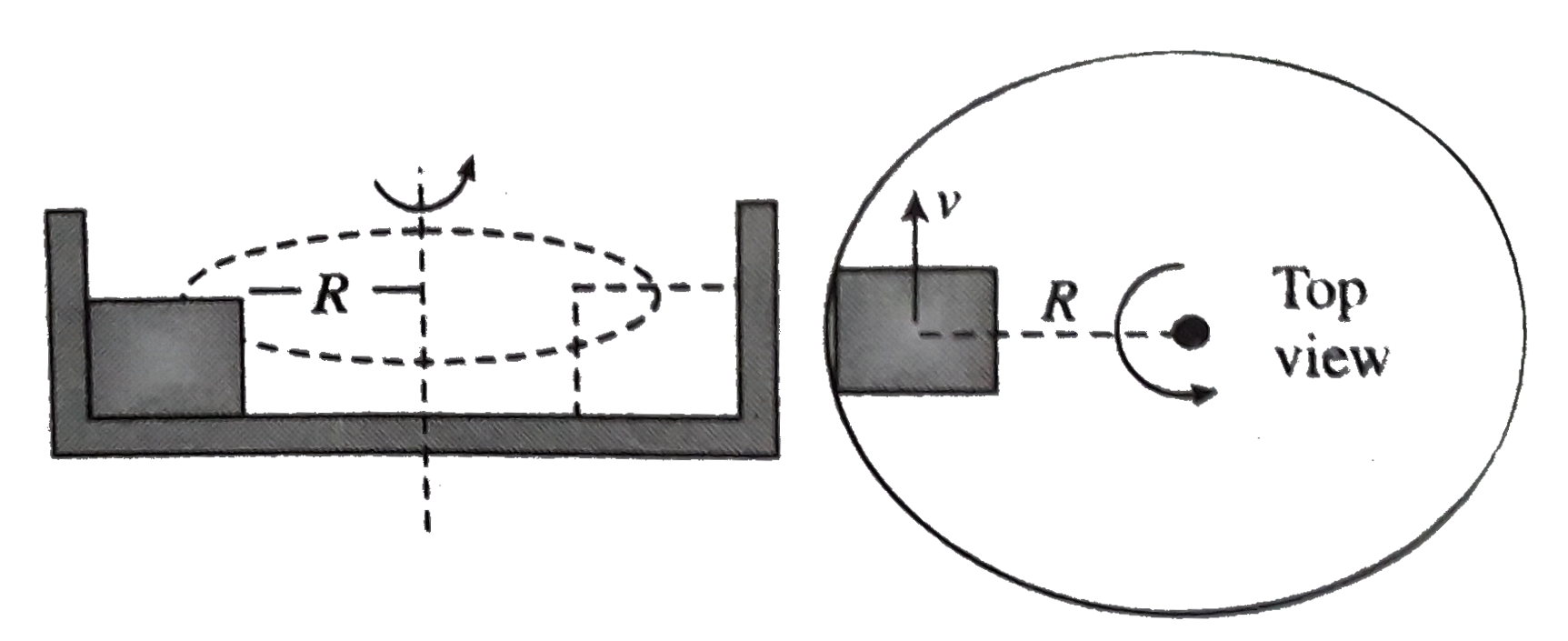
A block of mass $m$ is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block

A

$\frac{m v^{2}}{R}$

B

$m g$

C

$m \sqrt{\frac{v^{4}}{R^{2}} + 4 g^{2}}$

D

$m \sqrt{\frac{v^{4}}{R^{2}} + g^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

FBD Let $N_{1} N_{2} ↑$ be the normal reaction offered by the vetrical and horizontal surface respectively $N_{1}$ pushes the block toward the center of circle and $N_{2}$ equilibrium the block in vertical by millifying the weight $m g^{- 2}$ ) force equation

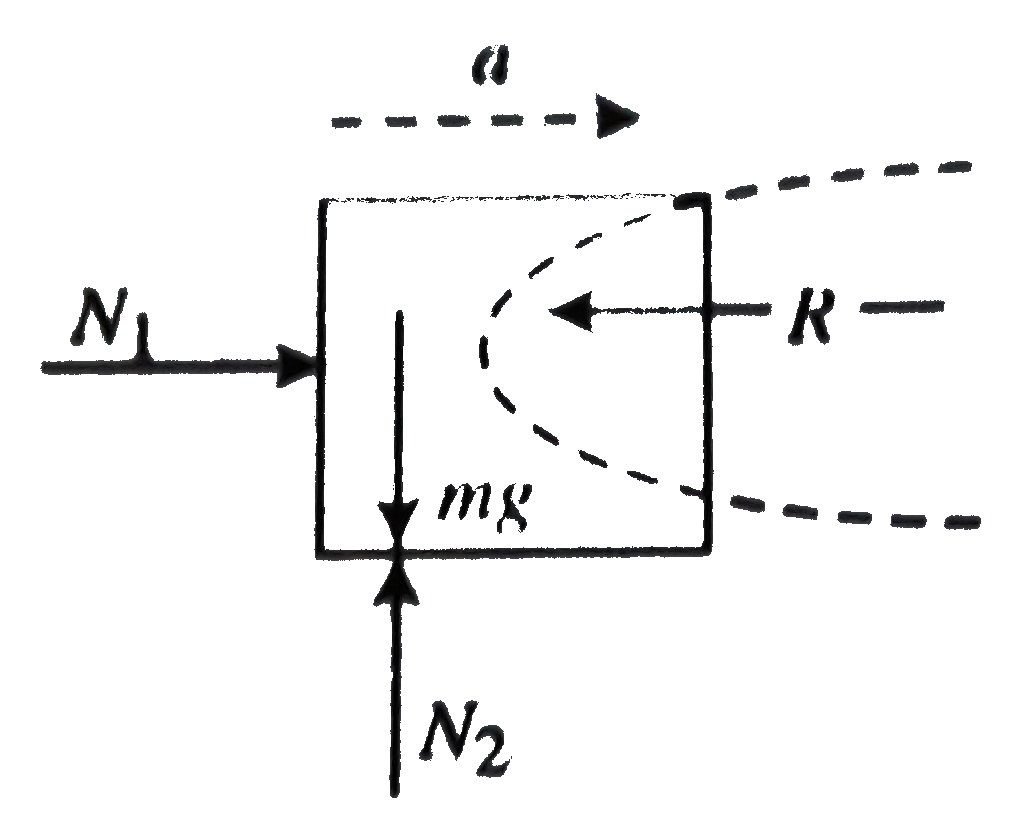
$N_{1} = m a_{1} = \frac{m v^{2}}{R}$ ...(i)
$N_{2} = m g$ ...(ii)
Hence the net reaction (contact) force is $\to N = {\to N}_{1} + {\to N}_{2}$
$∣ ∣ \to N ∣ ∣ = ∣ ∣ {\to N}_{2} ∣ ∣ = \sqrt{N_{2}^{2} + N_{1}^{2}}$
Substinuting $N_{1} and N_{2}$ we have
$N = m \sqrt{\frac{v^{4}}{R^{2}} + g^{2}}$

Updated on:21/07/2023

|

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

A body of mass m is moving in a circle of radius r with a constant speed v. The work done by the centripetal force in moving the body over half the circumference of the circle is
A $m v^{2} / r$
Bzero
C $m v^{2} / r$
D $r^{2} / m v^{2}$

CENGAGE PHYSICS ENGLISH-NEWTON'S LAWS OF MOTION 2-Single Correct

Home
Ask Doubt
Profile