Consider an 1100 particels gas system with speeds distribution as follows :
1000 particles each with speed 100m/s
2000 particles each wityh speed 200m/s
4000 particles each with speed 300m/s
3000 particles each with speed 400m/s and 1000 particles each with speed 500m/s
Find the average speed, and rms speed.
The correct Answer is:A, B, C
To solve the problem of finding the average speed and the root mean square (RMS) speed of a gas system with given particle speeds and their distributions, we can follow these steps:
Step 1: Identify the given data
We have the following data for the gas particles:
- 1000 particles with speed V1=100m/s
- 2000 particles with speed V2=200m/s
- 4000 particles with speed V3=300m/s
- 3000 particles with speed V4=400m/s
- 1000 particles with speed V5=500m/s
Step 2: Calculate the total number of particles
The total number of particles N is the sum of all particles:
N=1000+2000+4000+3000+1000=11000
Step 3: Calculate the average speed
The formula for average speed ¯V is given by:
¯V=N1V1+N2V2+N3V3+N4V4+N5V5N
Substituting the values:
¯V=1000×100+2000×200+4000×300+3000×400+1000×50011000
Calculating each term:
- 1000×100=100000
- 2000×200=400000
- 4000×300=1200000
- 3000×400=1200000
- 1000×500=500000
Adding these values:
100000+400000+1200000+1200000+500000=3200000
Now, substituting back into the average speed formula:
¯V=320000011000≈290.91m/s
Step 4: Calculate the RMS speed
The formula for RMS speed Vrms is given by:
Vrms=√N1V21+N2V22+N3V23+N4V24+N5V25N
Substituting the values:
Vrms=
⎷1000×1002+2000×2002+4000×3002+3000×4002+1000×500211000
Calculating each term:
- 1000×1002=10000000
- 2000×2002=80000000
- 4000×3002=360000000
- 3000×4002=480000000
- 1000×5002=250000000
Adding these values:
10000000+80000000+360000000+480000000+250000000=1170000000
Now, substituting back into the RMS speed formula:
Vrms=√117000000011000≈√106363.6363≈326.13m/s
Final Results
- Average Speed ¯V≈290.91m/s
- RMS Speed Vrms≈326.13m/s
We have the following data for the gas particles:
- 1000 particles with speed V1=100m/s
- 2000 particles with speed V2=200m/s
- 4000 particles with speed V3=300m/s
- 3000 particles with speed V4=400m/s
- 1000 particles with speed V5=500m/s
The total number of particles N is the sum of all particles:
N=1000+2000+4000+3000+1000=11000
The formula for average speed ¯V is given by:
¯V=N1V1+N2V2+N3V3+N4V4+N5V5N
Substituting the values:
¯V=1000×100+2000×200+4000×300+3000×400+1000×50011000
Calculating each term:
- 1000×100=100000
- 2000×200=400000
- 4000×300=1200000
- 3000×400=1200000
- 1000×500=500000
100000+400000+1200000+1200000+500000=3200000
Now, substituting back into the average speed formula:
¯V=320000011000≈290.91m/s
The formula for RMS speed Vrms is given by:
Vrms=√N1V21+N2V22+N3V23+N4V24+N5V25N
Substituting the values:
Vrms=
⎷1000×1002+2000×2002+4000×3002+3000×4002+1000×500211000
Calculating each term:
- 1000×1002=10000000
- 2000×2002=80000000
- 4000×3002=360000000
- 3000×4002=480000000
- 1000×5002=250000000
10000000+80000000+360000000+480000000+250000000=1170000000
Now, substituting back into the RMS speed formula:
Vrms=√117000000011000≈√106363.6363≈326.13m/s
- Average Speed ¯V≈290.91m/s
- RMS Speed Vrms≈326.13m/s
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Example Type 11videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Example Type 21videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason2videos
UNIT AND DIMENSIONS
Similar Questions
Find average speed of 40m/s and 50m/s.
View SolutionA man travels 200 km distance with the speed of 40 m/s and next 50 km with the speed of 10 m/s . Find the average speed of man.
View SolutionDefine average speed and r.m.s. speed of a gas molecule.
View SolutionA particle moves along x-axis with speed 6m/s for the first half distance of a journey and the second half distance with a speed 3m/s. The average speed in the total journey is
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:
 View Solution
View SolutionA car moves a distance of 100 m. It coveres first half with speed of 10 m/s and another half with speed of v m/s. If the average speed of car is 18 m/s, then value of v is
View Solutions-t graph of a particle in motion is shown in Fig. Calculate
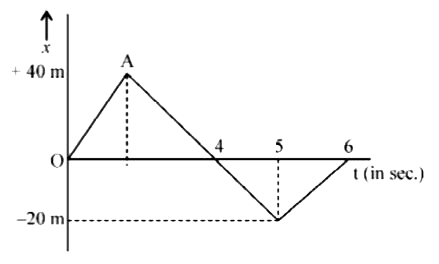
Average speedView SolutionA particle travels half of the time with constant speed 2m/s, In remaining half of the time it travels, 14th distance with constant speed of 4m/s and 34th distance with 6m/s. Find average speed during the complete journey.
View SolutionFour particles have speed 2,3,4 and 5 cm/s respectively Their RMS speed is .
View SolutionA particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
View Solution

