Choose the wrong options
Translational kinetic energy of all ideal gases at same temperature is same.
In one degree of freedom all ideal gases has interal energy = 12RT
Translational degree of freedom of all ideal gases is three
Translational kinetic energy of one mole of all ideal gases is 32RT
The correct Answer is:A, B
To solve the question of choosing the wrong options regarding the translational kinetic energy and internal energy of ideal gases, we will analyze the statements one by one.
1. Understanding Translational Kinetic Energy:
- The translational kinetic energy of an ideal gas is given by the formula:
KE=F2RT
where F is the number of degrees of freedom, R is the gas constant, and T is the temperature in Kelvin.
2. Degrees of Freedom:
- For ideal gases, the degrees of freedom for translational motion is 3 (x, y, z directions). Therefore, the translational kinetic energy for one mole of an ideal gas is:
KE=32RT
- This means that the translational kinetic energy of all ideal gases at the same temperature is indeed the same, which makes this statement true.
3. Internal Energy of Ideal Gases:
- The internal energy U of an ideal gas is given by:
U=F2RT
- For one degree of freedom, the internal energy would be:
U=12RT
- However, the statement in the question claims that for one degree of freedom, the internal energy is 12RT for all ideal gases, which is misleading. The correct expression for one molecule in one degree of freedom is:
U=12kT
- Therefore, the statement regarding the internal energy being 12RT for one degree of freedom is false.
4. Conclusion:
- Based on the analysis, the wrong option is the one that states "in one degree of freedom, all ideal gases' internal energy is equal to 12RT". This is incorrect because the correct expression should involve the Boltzmann constant k for a single molecule and not R for one mole.
Final Answer:
The wrong option is Option B.
---
- The translational kinetic energy of an ideal gas is given by the formula:
KE=F2RT
where F is the number of degrees of freedom, R is the gas constant, and T is the temperature in Kelvin.
- For ideal gases, the degrees of freedom for translational motion is 3 (x, y, z directions). Therefore, the translational kinetic energy for one mole of an ideal gas is:
KE=32RT
- This means that the translational kinetic energy of all ideal gases at the same temperature is indeed the same, which makes this statement true.
- The internal energy U of an ideal gas is given by:
U=F2RT
- For one degree of freedom, the internal energy would be:
U=12RT
- However, the statement in the question claims that for one degree of freedom, the internal energy is 12RT for all ideal gases, which is misleading. The correct expression for one molecule in one degree of freedom is:
U=12kT
- Therefore, the statement regarding the internal energy being 12RT for one degree of freedom is false.
- Based on the analysis, the wrong option is the one that states "in one degree of freedom, all ideal gases' internal energy is equal to 12RT". This is incorrect because the correct expression should involve the Boltzmann constant k for a single molecule and not R for one mole.
The wrong option is Option B.
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Single Correct
12 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
A small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionThe vessel shown in the figure has a two sections of areas of cross-section A1 and A2. A liquid of density ρ fills both th sections, up to a height h in each Neglect atmospheric pressure. Choose the wrong option.
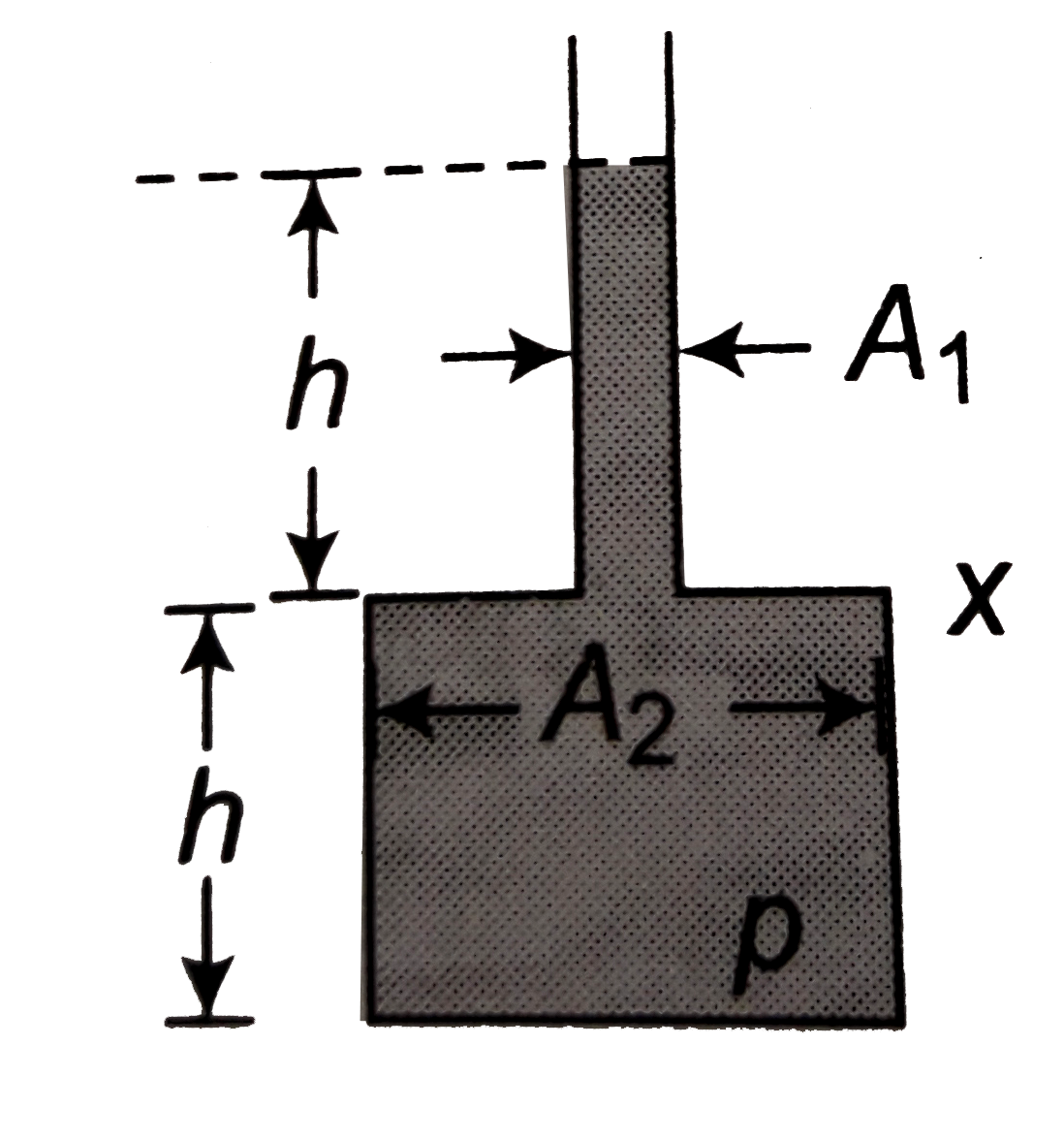 .
.
View SolutionPassage V) In SHM displacement, velocity and acceleration all oscillate simple harmonically with same angular frequency ω. Phase difference between any two is π2 except that between displacement and acceleration which is π.
v-t graph of a particle is SHM is as shown in figure Choose the wrong option.

View SolutionAn object is weighted at the North Pole by a beam balance and a spring balance, giving readings of WB and WS respectively. It is again weighed in the same manner at the equator, giving readings of W'B and W'S respectively. Assume that the acceleration due to gravity is the same everywhere and that the balance are quite sensitive, Choose the wrong option
View SolutionA block of mass m is at rest on wedge as shown in figure. Let N be the normal reaction between two and f the force of friction, then choose the wrong option.
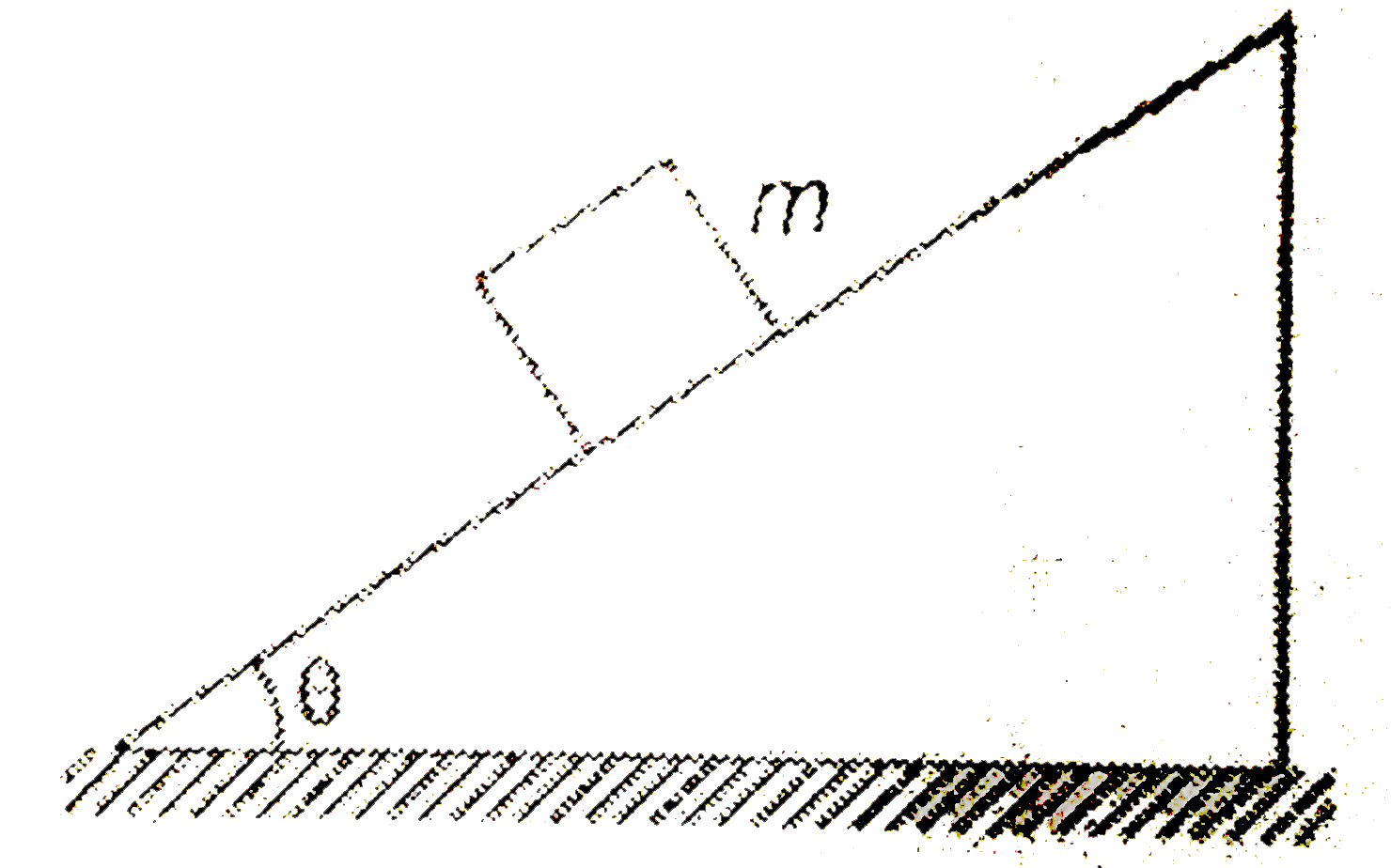
View SolutionA ball of mass 'm' is rotating in a circle of radius 'r' with speed v inside a smooth cone as shown in figure. Let N be the normal reaction on the ball by the cone .then choose the wrong option.

View SolutionChoose the wrong pair
View SolutionChoose the wrong one on the basis of Bohr 's theory :-
View SolutionChoose the wrong match
View SolutionChoose the wrong alternative.
View Solution