Choose the correct options.
In p=mMRT, (m) is mass of gas per unit volume.
In pV=mMRT, (m) is mass of one molecule of gas.
In p=13mNVv2rms, (m) is total mass of gas.
In vrms=√3kTm , (m) is mass of one molecule of gas.
The correct Answer is:A, D
To solve the question of choosing the correct options related to the ideal gas equation and properties of gases, we will analyze each option step by step.
1. Understanding the Ideal Gas Equation:
The ideal gas equation is given by:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is temperature.
2. Analyzing Option A:
The first option states:
P=mMRT
Here, m is the mass of gas per unit volume. We can express n (number of moles) as:
n=mM
where M is the molar mass. Substituting this into the ideal gas equation gives:
PV=(mM)RT
Dividing both sides by V:
P=mMVRT
For unit volume, V=1:
P=mMRT
Thus, this option is correct.
3. Analyzing Option B:
The second option states:
m is the mass of one molecule of gas.
In the previous derivation, m represents the total mass of the gas, not the mass of one molecule. Therefore, this option is incorrect.
4. Analyzing Option C:
The third option states:
P=13mnVv2rms
Here, vrms is the root mean square velocity. We know:
vrms=√3RTM
Substituting this into the equation:
P=13mnV(3RTM)
Simplifying gives:
P=mnRTMV
Here, m is the mass of one molecule, and n is Avogadro's number. Therefore, this option incorrectly states m as the total mass of gas. Thus, this option is incorrect.
5. Analyzing Option D:
The fourth option states:
vrms=√3RTm
Here, m is claimed to be the mass of one molecule. We know:
vrms=√3kTm
where k is Boltzmann's constant. Since m is indeed the mass of one molecule, this option is correct.
Final Conclusion:
- Correct Options: A and D
- Incorrect Options: B and C
The ideal gas equation is given by:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is temperature.
The first option states:
P=mMRT
Here, m is the mass of gas per unit volume. We can express n (number of moles) as:
n=mM
where M is the molar mass. Substituting this into the ideal gas equation gives:
PV=(mM)RT
Dividing both sides by V:
P=mMVRT
For unit volume, V=1:
P=mMRT
Thus, this option is correct.
The second option states:
m is the mass of one molecule of gas.
In the previous derivation, m represents the total mass of the gas, not the mass of one molecule. Therefore, this option is incorrect.
The third option states:
P=13mnVv2rms
Here, vrms is the root mean square velocity. We know:
vrms=√3RTM
Substituting this into the equation:
P=13mnV(3RTM)
Simplifying gives:
P=mnRTMV
Here, m is the mass of one molecule, and n is Avogadro's number. Therefore, this option incorrectly states m as the total mass of gas. Thus, this option is incorrect.
The fourth option states:
vrms=√3RTm
Here, m is claimed to be the mass of one molecule. We know:
vrms=√3kTm
where k is Boltzmann's constant. Since m is indeed the mass of one molecule, this option is correct.
- Correct Options: A and D
- Incorrect Options: B and C
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective9videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Single Correct12videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason2videos
UNIT AND DIMENSIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the following
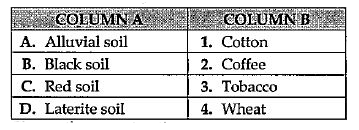
Choose the correct option:AA-3, B-2, C-1, D-4BA-4, B-1, C-3, D-2CA-2, B-4, C-1, D-3DA-4, B-1, C-2, D-3 - Question 2 - Select One
Match the following
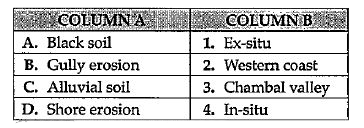
Choose the correct option:AA-1, B-3, C-4, D-2BA-4, B-1, C-3, D-2CA-2, B-4, C-1, D-3DA-4, B-3, C-1, D-2
Choose the correct option(s) for the given sitution.
 View Solution
View SolutionMatch the following and choose the correct option.
 View Solution
View SolutionObserve figures and choose the correct option.
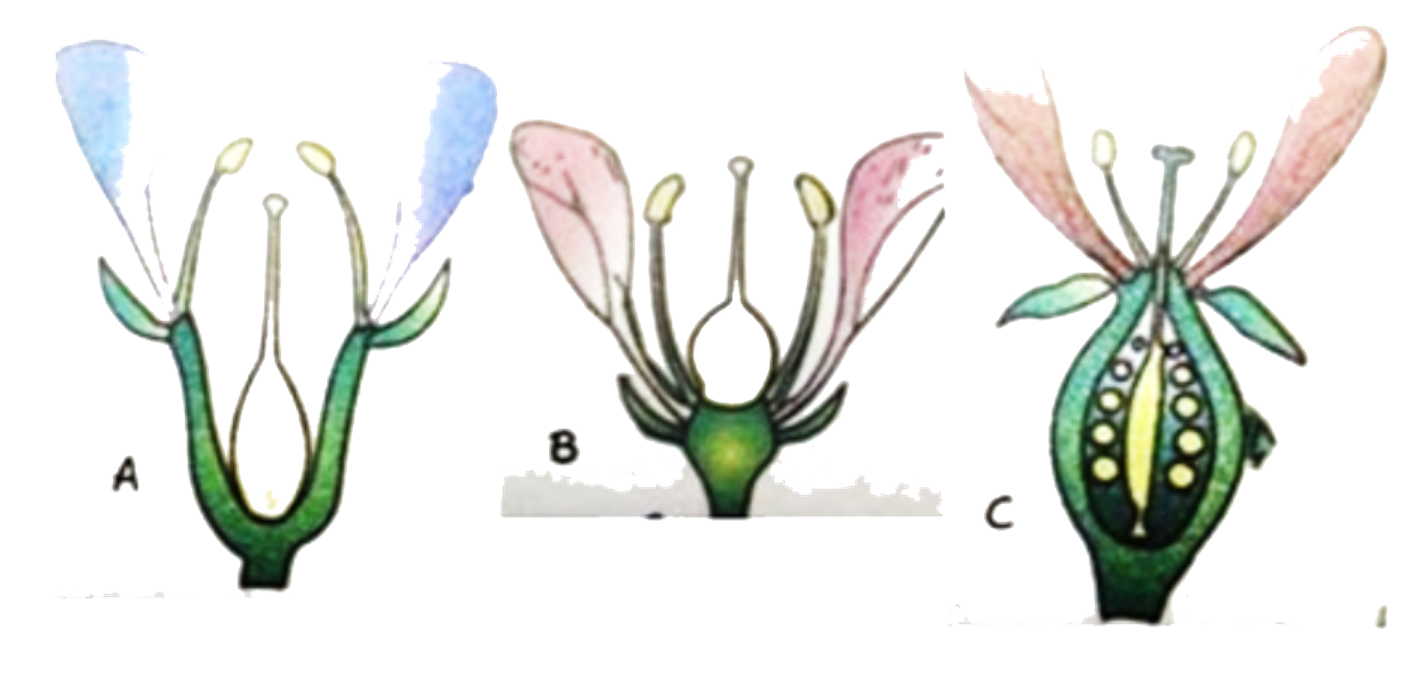 View Solution
View SolutionMatch the following and choose the correct option.
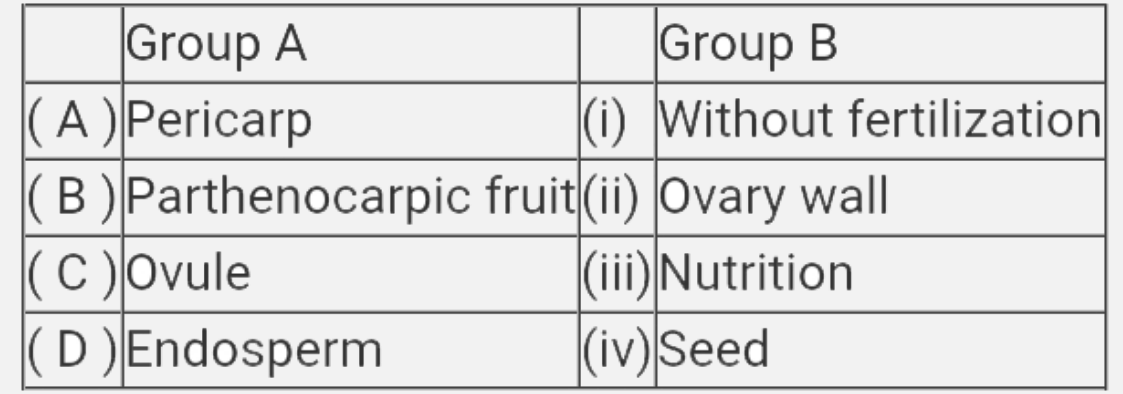 View Solution
View SolutionStudy the following flow chart and choose the correct option.
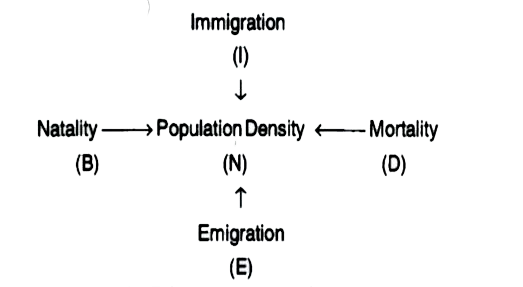 View Solution
View SolutionConsider the diagram given below and choose the correct option.
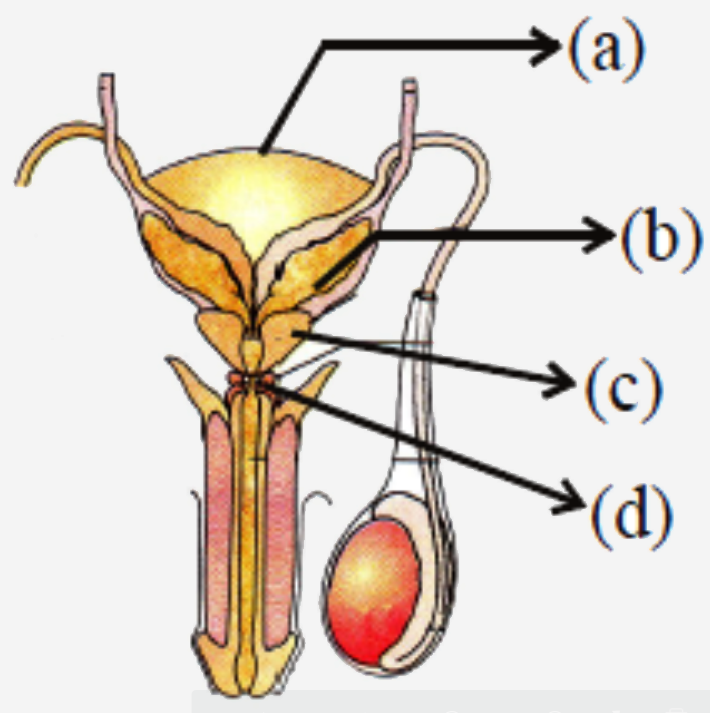 View Solution
View Solution


_CHE_E06_278.png) Choose the correct option.
Choose the correct option.