Starting with the same initial conditions, an ideal gas expands from volume V1 to V2 in three different ways, the work done by the gas is W1 if the process is purely isothermal, W2 if purely isobaric and W3 if purely adiabatic, then
(a) W2>W1>W3
(b) W2>W3>W1
(c) W1>W2>W3
(d) W1>W3>W2
The correct Answer is:A
To find the relationship between the work done by an ideal gas during expansion in three different processes (isothermal, isobaric, and adiabatic), we can analyze the work done in each process using the area under the pressure-volume (P-V) curves.
1. Understanding the Processes:
- Isothermal Process (W1): The gas expands at a constant temperature. The P-V curve is a hyperbola. The work done can be calculated using the formula:
W1=nRTln(V2V1)
- Isobaric Process (W2): The gas expands at a constant pressure. The P-V curve is a horizontal line. The work done is given by:
W2=P(V2−V1)
- Adiabatic Process (W3): The gas expands without heat exchange. The P-V curve is steeper than the isothermal curve. The work done can be calculated using the formula:
W3=P1V1−P2V2γ−1
where γ is the heat capacity ratio (C_p/C_v).
2. Analyzing the Areas Under the Curves:
- The work done by the gas in each process corresponds to the area under the respective P-V curve.
- For the isobaric process (W2), the area is the largest because it represents a constant pressure over a change in volume.
- The isothermal process (W1) has a smaller area than the isobaric process but larger than the adiabatic process (W3).
- The adiabatic process (W3) has the smallest area under the curve, indicating the least work done.
3. Establishing the Relationship:
- From the analysis of the areas under the curves, we can conclude:
W2>W1>W3
- This means that the work done during the isobaric process is greater than that done during the isothermal process, which in turn is greater than that done during the adiabatic process.
Final Relation:
Thus, the relationship between the work done in the three processes is:
W2>W1>W3
- Isothermal Process (W1): The gas expands at a constant temperature. The P-V curve is a hyperbola. The work done can be calculated using the formula:
W1=nRTln(V2V1)
- Isobaric Process (W2): The gas expands at a constant pressure. The P-V curve is a horizontal line. The work done is given by:
W2=P(V2−V1)
- Adiabatic Process (W3): The gas expands without heat exchange. The P-V curve is steeper than the isothermal curve. The work done can be calculated using the formula:
W3=P1V1−P2V2γ−1
where γ is the heat capacity ratio (C_p/C_v).
- The work done by the gas in each process corresponds to the area under the respective P-V curve.
- For the isobaric process (W2), the area is the largest because it represents a constant pressure over a change in volume.
- The isothermal process (W1) has a smaller area than the isobaric process but larger than the adiabatic process (W3).
- The adiabatic process (W3) has the smallest area under the curve, indicating the least work done.
- From the analysis of the areas under the curves, we can conclude:
W2>W1>W3
- This means that the work done during the isobaric process is greater than that done during the isothermal process, which in turn is greater than that done during the adiabatic process.
Thus, the relationship between the work done in the three processes is:
W2>W1>W3
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 12videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Example Type 21videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions10videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
Starting from the same initial conditions, an ideal gas expands from volume V1→V2 in three different ways. The work done by the gas is W1 if he process is purely isothermal, W2 if purely isobaric and W3 if purely adiabatic. Then
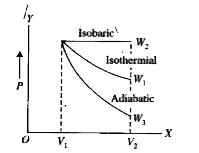 AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2
AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2 - Question 2 - Select One
A gas expands from i to f along the three paths indicated. The work done along the three paths denoted by W1,W2andW3 have the relationship
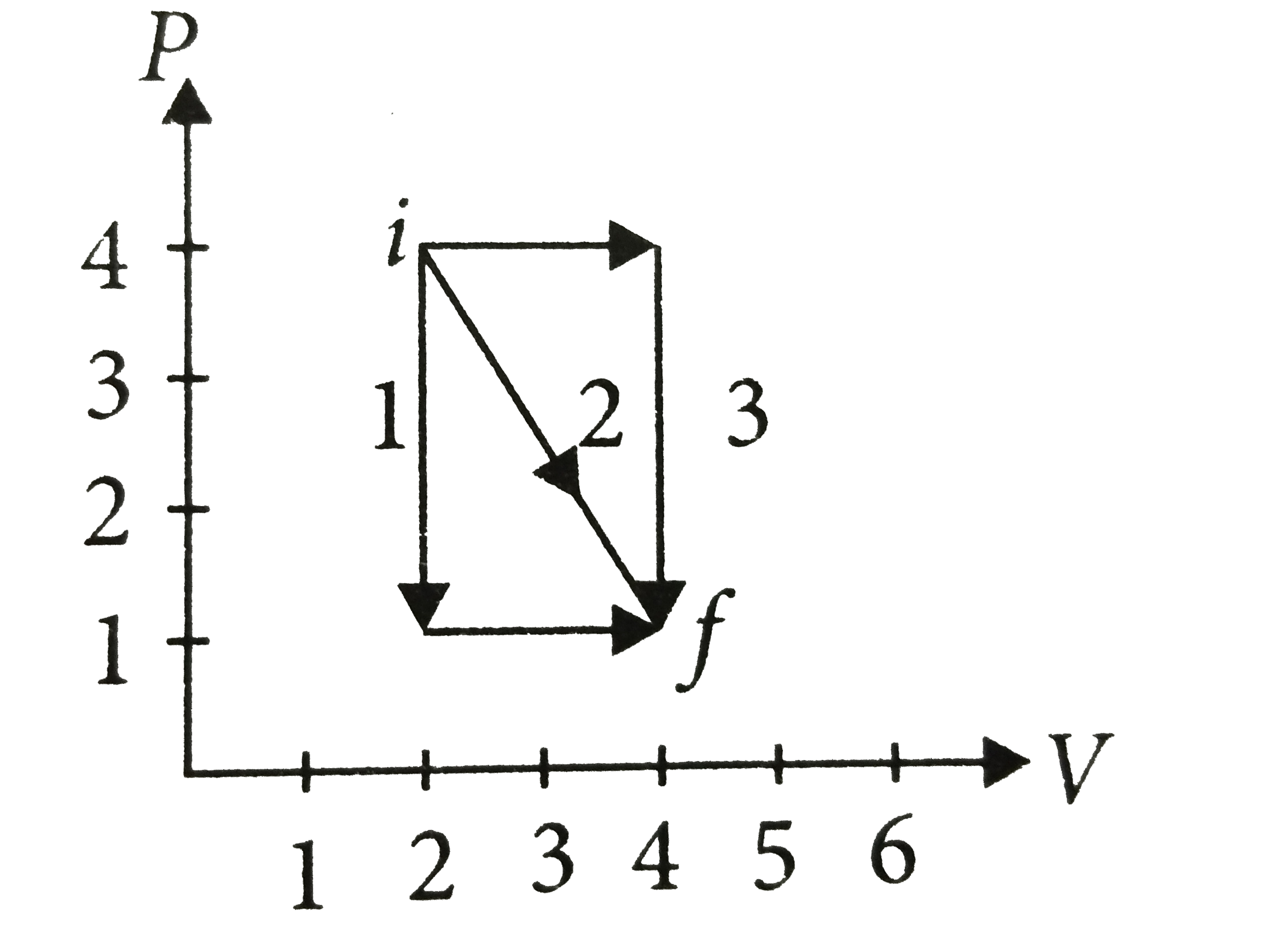 AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3
AW1<W2<W3BW2<W1=W3CW2<W1<W3DW1>W2>W3
The work done by 1 mole of ideal gas during an adiabatic process is (are ) given by :
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
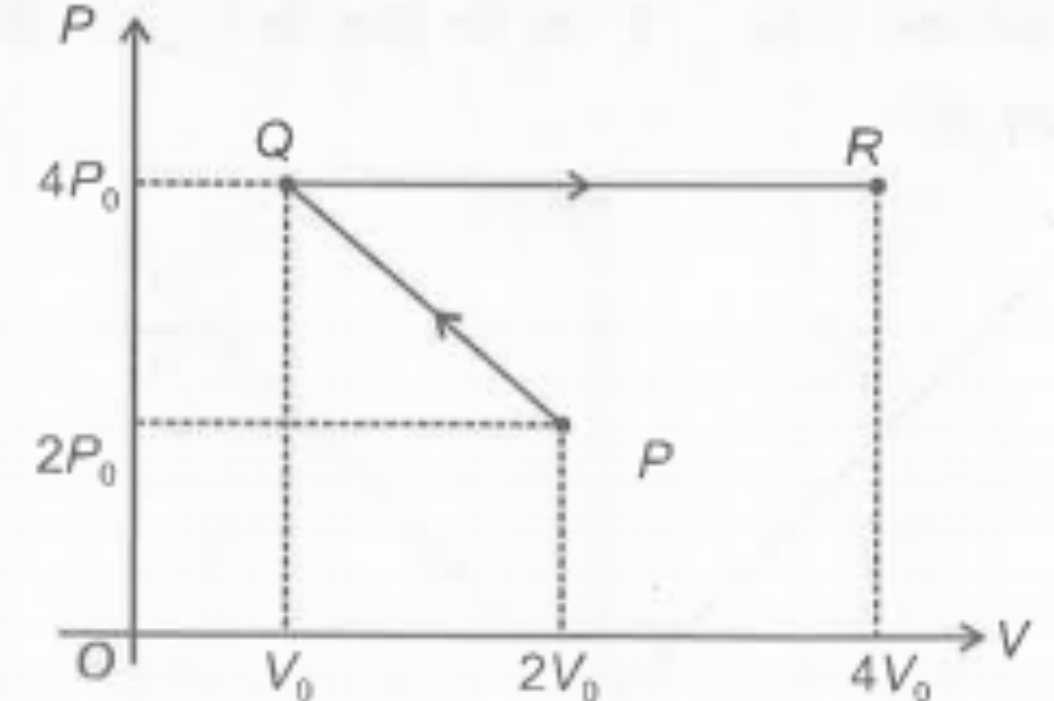 View Solution
View Solution2 mol of an ideal gas at 27∘C expand isothermally and reversibly
from a volume of 2L to 20L. The work done (in KJ) by the gas is :-View SolutionLet Q and W denote the amount of heat given to an ideal gas the work done by it in an isothermal process.
View SolutionIf x mole of ideal gas at 27∘C expands isothermally and reversibly from a volume of y to 10 y, then the work done is
View SolutionAn ideal gas has initial volume V and pressure p. In doubling its volume the minimum work done will be in the process (of the given processes)
View Solution

