A sample of gas expands from volume V1 to V2. The amount of work done by the gas is greatest when the expansion is
adiabatic
isobaric
isothermal
Equal in all above cases
The correct Answer is:b
To determine when the work done by a gas during expansion is greatest, we need to analyze the different thermodynamic processes: isobaric, isothermal, and adiabatic.
1. Understanding Work Done in Thermodynamics:
The work done by a gas during expansion can be expressed mathematically as:
W=∫V2V1PdV
where W is the work done, P is the pressure, and V1 and V2 are the initial and final volumes, respectively.
2. Identifying Different Processes:
- Isobaric Process: The pressure remains constant during the expansion. The work done is given by:
W=P(V2−V1)
- Isothermal Process: The temperature remains constant. The pressure changes according to the ideal gas law, and the work done is:
W=nRTln(V2V1)
- Adiabatic Process: No heat is exchanged with the surroundings. The work done is less than in the isothermal process because the pressure decreases more rapidly than in the isothermal case.
3. Comparing Work Done:
- In the isobaric process, since the pressure is constant, the work done is directly proportional to the change in volume, which can be quite significant.
- In the isothermal process, while the work done can be substantial, it is dependent on the logarithmic relationship and may not be as high as in the isobaric case for the same volume change.
- In the adiabatic process, the work done is the least because the pressure drops significantly as the gas expands.
4. Conclusion:
The work done by the gas is greatest during an isobaric expansion because the pressure remains constant, allowing for maximum work output for a given change in volume.
Final Answer:
The amount of work done by the gas is greatest when the expansion is isobaric.
The work done by a gas during expansion can be expressed mathematically as:
W=∫V2V1PdV
where W is the work done, P is the pressure, and V1 and V2 are the initial and final volumes, respectively.
- Isobaric Process: The pressure remains constant during the expansion. The work done is given by:
W=P(V2−V1)
- Isothermal Process: The temperature remains constant. The pressure changes according to the ideal gas law, and the work done is:
W=nRTln(V2V1)
- Adiabatic Process: No heat is exchanged with the surroundings. The work done is less than in the isothermal process because the pressure decreases more rapidly than in the isothermal case.
- In the isobaric process, since the pressure is constant, the work done is directly proportional to the change in volume, which can be quite significant.
- In the isothermal process, while the work done can be substantial, it is dependent on the logarithmic relationship and may not be as high as in the isobaric case for the same volume change.
- In the adiabatic process, the work done is the least because the pressure drops significantly as the gas expands.
The work done by the gas is greatest during an isobaric expansion because the pressure remains constant, allowing for maximum work output for a given change in volume.
The amount of work done by the gas is greatest when the expansion is isobaric.
Similar Questions
Starting with the same initial conditions, an ideal gas expands from volume V1 to V2 in three different ways, the work done by the gas is W1 if the process is purely isothermal, W2 if purely isobaric and W3 if purely adiabatic, then
View SolutionAn ideal gas is allowed to expand against a constant pressure of 2 bar from 10L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case ?
(Give that, 1 L bar = 100 J)
View Solution
Knowledge Check
Starting from the same initial conditions, an ideal gas expands from volume V1→V2 in three different ways. The work done by the gas is W1 if he process is purely isothermal, W2 if purely isobaric and W3 if purely adiabatic. Then
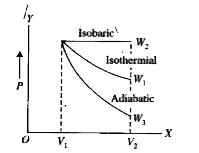 AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2
AW2>W1>W3BW2>W3>W1CW1>W2>W3DW1>W3>W2
The magnitude of ethalphy changes for reversible adiabatic expansion of a gas from volume V1 to V2(in L)is ΔH1 and for irreversible adiabatic expansion for the same expansion is ΔH2. Then
when ΔU1 and ΔU2 are the changes in magnitudes for the internal energy of gas in the two expansions.
View SolutionThe number of correct statements among the following
1 The expansion work for a gas into vacuum is equal to zero.
2. 1 mole of a gas occupying 3 litre volume on expanding to 15 litre at constant pressure of 1 atm does expansion work 1.215kJ.
3. The maximum work done by the gas during reversible expansionof 16g O2 at 300K from 5dm3 to 25dm3 is 2.0074 kJ.
4. The ΔSfor s→l is almost negligible in comparison to ΔS for l→g.
5. ΔS=2.303nRlogV2V1 (at constant T)
6. Reversible isothermal work done =−2.303nRTlog10V2V1
View SolutionA gas can expand from 100mL to 250mL under a constant pressure of 2 atm. The work done by the gas is
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) is
View SolutionFind the expression for the work done by a system undergoing isothermal compression (or expansion) from volume V1 to V2 at temperature T0 for a gas which obeys the van der waals equation of state. (P+an2/V2)(V−bn)=nRT?
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View SolutionThe figures given below show different processes (relating pressure P and volume V) for a given amount of an ideal gas. W is work done by the gas and ΔQ is heat absorbed by the gas.
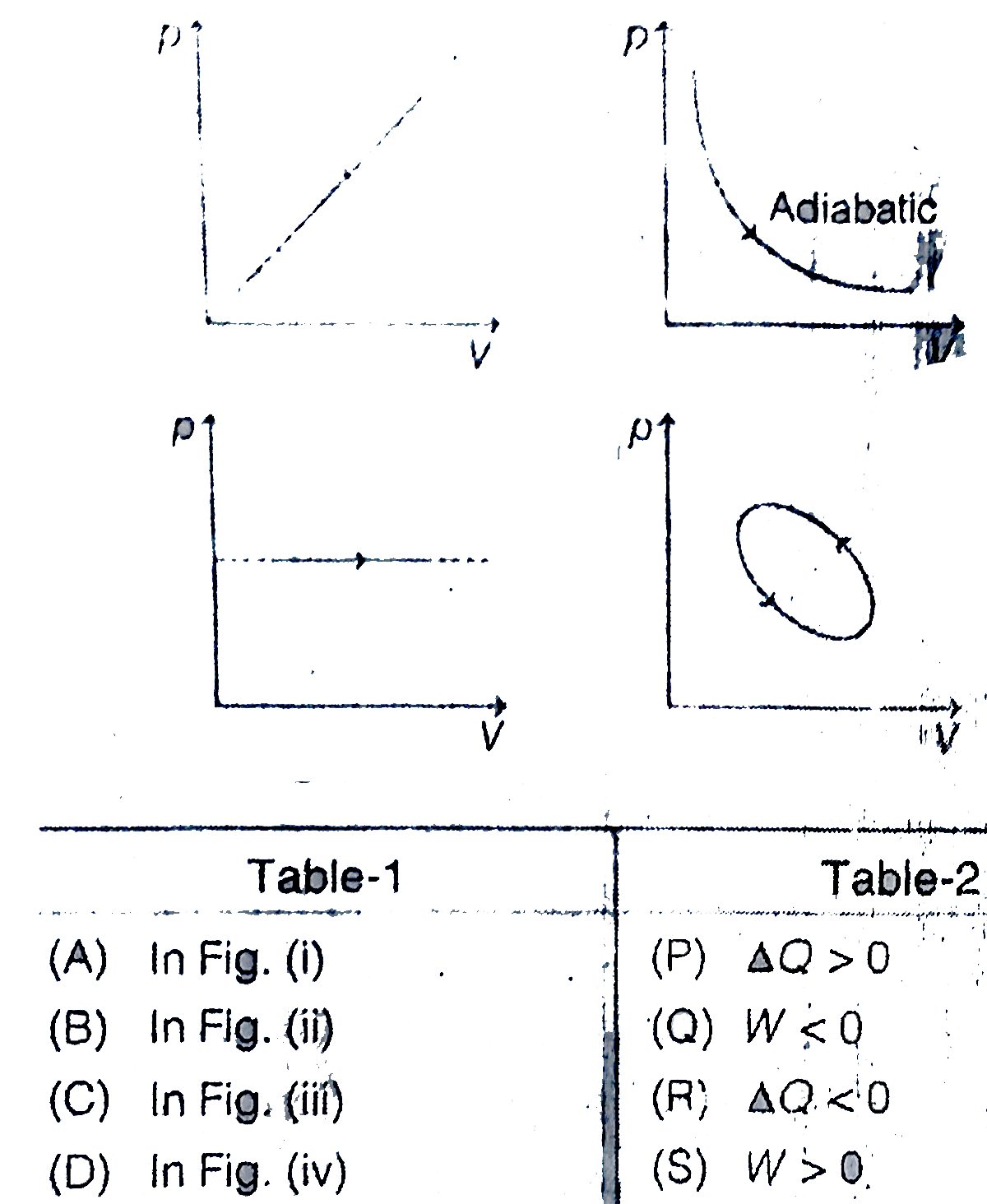
View Solution
