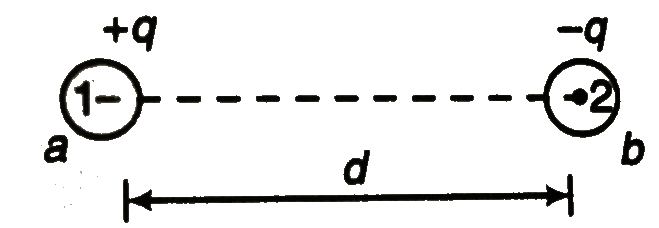
a. Two spheres have radii a and b and their centres are at a distance d apart. Show that the capacitance of this system is
C=4πε01a+1b±2d
provided that d is large compared with a and b.
b. Show that as d approaches infinity the above result reduces to that of two islotated spheres inseries.
a. PD,V=V1+V2
=14πε0[(qa−qd)−(−qb+qd)
∴C=qV−4πε01a+1b−2d
If −q is given to first shere and +q to second sphere, then
C=4πε01a+1b+2d
b. If d→∞, then C=4πε01a+1b=(4πε0)(ab)a+b
in series, C≠t=C1C2C1+C2=(4πε0a)(4πε0b)(4πε0a)+(4πε0b)=((4πε0)aba+b)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise155videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
Two metal spheres of radius r have centers at a distance d apart in air. Find the capacitance of the system.
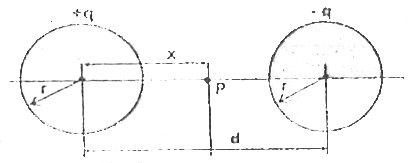 View Solution
View SolutionTwo metal spheres of radii a and b are connected by a thin wire. Their separation is very large compared to their dimensions. The capacitance of this system is
View SolutionIn figure, AB>AC. Show that AB>AD.
View SolutionTwo metal spheres A and B of radii a & b (a < b) respectively are at a large distance apart. Each sphere carries a charge of 100μO. the sphere are connected by a conducting wire, then
View SolutionThere are two conducting spheres of radius a and b (b>a) carrying equal and opposite charges. They are placed at a separation d (>>> a and b). The capacitance of system is
 View Solution
View SolutionTwo chords AB and CD of a circle are parallel and a line L is the perpendicular bisector of AB. Show that L bisects CD
View SolutionIn Figure, AB>AC. Show that AB>AD.
View SolutionIf a,b,c,d are in G. P., show that <br>a+b,b+c,c+dare also in G. P.
View SolutionAD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionTwo homogeneous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch . The distance of the centre of mass from the first sphere is
View Solution

