Two metal spheres A and B of radii a & b (a < b) respectively are at a large distance apart. Each sphere carries a charge of 100μO. the sphere are connected by a conducting wire, then
Charge will flow from A to B
Charge will flow from B to A
NO charge flows in the wire
All charges will reside on the connecting wire
The correct Answer is:A
To solve the problem step by step, let's analyze the situation involving the two metal spheres A and B, which are connected by a conducting wire.
Step 1: Understand the initial conditions
- We have two metal spheres, A and B, with radii a and b respectively, where a<b.
- Each sphere carries a charge of Q=100μC.
Step 2: Calculate the electric potential of each sphere
The electric potential V on the surface of a charged sphere is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the radius of the sphere.
- For sphere A (radius a):
VA=k⋅100×10−6a
- For sphere B (radius b):
VB=k⋅100×10−6b
Step 3: Compare the potentials
Since a<b and both spheres have the same charge Q, we can compare the potentials:
- Since b>a, it follows that:
VA>VB
This means sphere A is at a higher potential than sphere B.
Step 4: Determine the direction of charge flow
When two conductors are connected by a wire, charge flows from the higher potential to the lower potential. Therefore, charge will flow from sphere A to sphere B.
Step 5: Conclusion
Thus, when the two spheres are connected by a conducting wire, the charge will flow from sphere A to sphere B.
Final Answer
The charge will flow from sphere A to sphere B.
---
- We have two metal spheres, A and B, with radii a and b respectively, where a<b.
- Each sphere carries a charge of Q=100μC.
The electric potential V on the surface of a charged sphere is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the radius of the sphere.
VA=k⋅100×10−6a
VB=k⋅100×10−6b
Since a<b and both spheres have the same charge Q, we can compare the potentials:
- Since b>a, it follows that:
VA>VB
This means sphere A is at a higher potential than sphere B.
When two conductors are connected by a wire, charge flows from the higher potential to the lower potential. Therefore, charge will flow from sphere A to sphere B.
Thus, when the two spheres are connected by a conducting wire, the charge will flow from sphere A to sphere B.
The charge will flow from sphere A to sphere B.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - C
Explore 53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - D
Explore 9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - A
Explore 44 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 15 Videos
Similar Questions
Two spherical conductors A and B of radii R and 2R respectively , are separated by a large distance . If some charge is given to both the spheres and later they are connected by a conducting wire , then in equilibrium condition , the ratio of the magnitude of the electric fields at the surface of spheres A and B is
View SolutionTwo conducting spheres of radii r and 2r are placed at very large separation. Each sphere possesses charge Q. These spheres are connected with a conducting wire of resistance R. Then, which of the following is true?
View SolutionTwo spherical conductors A and B of radii 1mm and 2mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is
View SolutionTwo small metal spheres A and B, each of radius r and supported on insulating stands, located at a distance a(a>>r) from each other are connected by a thin conducting wire. A point charge q is brought near the spheres at distance l(l>>r) on the line joining the centers of the spheres. What are the moduli of charge induced on the spheres ?
 .
.
View SolutionTwo spheres A and B of radius 'a' and 'b' respectively are at same electric potential. The ratio of the surface charge densities of A and B is
View SolutionTwo spherical conductors of radii R1andR2 are separated by a distance much larger than the radius of eighter sphere. The spheres are connected by a conducting wire as shown in (Fig. 3.128). If the charges on the spheres in equilibrium are q1andq2, respectively, what is the ratio of the field strength at the surfaces of the spheres ?
 .
.
View SolutionTwo fixed identical metallic spheres A and B of radius R=50cm each are placed on a non-conducting plane at a very large distance from each other and they are connected by a coil of inductance L=9mH as shown in figure. One of the spheres (say A) is imparted an initial charge and the other is kept uncharged. The switch S is closed at t=0. After what minimum time t does the charge on the first sphere decrease to half of its initial value ?
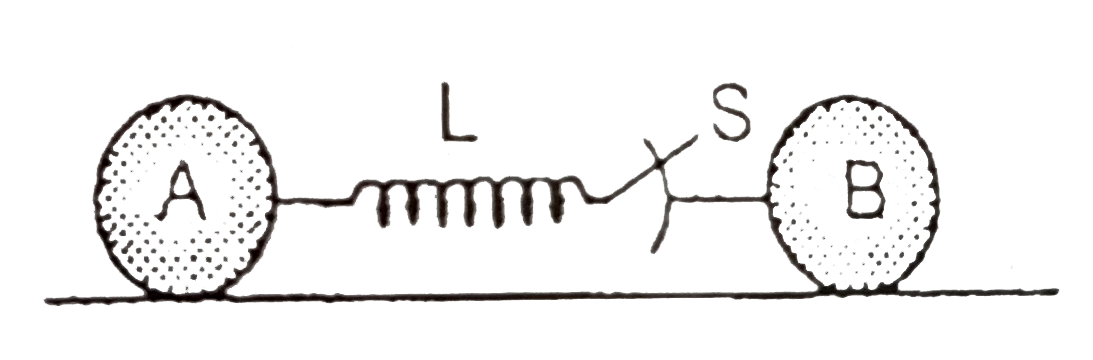
View SolutionTwo conducting spheres of radii 6km and 12km each, having the same charge 3×10−8C, are kept very far apart. If the spheres are connected to each other by a conductiong wire, find
i. the direction and amount of charge transferred and
ii. final potential each sphere.
View SolutionConsider Two metallic charged sphere whose radii are 20 cm and 10 cm respectively each having 150 microcoulomb positive charge. What is their common potential after they are connected by a conducting wire ?
View SolutionTwo isolated metallic solid spheres of radii R and 2R are charged such that both of these have same charge density σ. The spheres are located far away from each other and connected by a thin conducting wire. Find the new charge density on the bigger sphere.
View Solution