A capacitor is given a charge . The distance between the plates of the capacitor is . One of the plates is fixed and the other plate is moved away from the other till the distance between them becomes . Find the work done by the external force.
The correct Answer is:A, B, D
To find the work done by the external force when one plate of a capacitor is moved away from the other, we can follow these steps:
Step 1: Understand the Initial Conditions
- We have a capacitor with charge q and plates separated by a distance d.
- One plate is fixed, and the other plate is moved away until the distance becomes 2d.
Step 2: Determine the Force on the Plates
- The force between the plates of a capacitor can be derived from the electric field E between the plates and the charge q on the plates.
- The electric field E between the plates is given by:
E=qϵ0A
where ϵ0 is the permittivity of free space and A is the area of the plates.
- The force F on one plate due to the electric field from the other plate is:
F=qE=q(qϵ0A)=q2ϵ0A
Step 3: Calculate the Work Done
- The work done W by the external force when moving the plate from distance d to 2d is given by:
W=F⋅ddisplacement
- The displacement ddisplacement in this case is 2d−d=d.
- Therefore, the work done by the external force is:
W=F⋅d=(q2ϵ0A)⋅d
Step 4: Final Expression for Work Done
- Substituting the values, we get:
W=q2dϵ0A
This is the work done by the external force in moving the plate from distance d to 2d.
Summary
The work done by the external force when one plate of a capacitor is moved from distance d to 2d is:
W=q2dϵ0A
- We have a capacitor with charge q and plates separated by a distance d.
- One plate is fixed, and the other plate is moved away until the distance becomes 2d.
- The force between the plates of a capacitor can be derived from the electric field E between the plates and the charge q on the plates.
- The electric field E between the plates is given by:
E=qϵ0A
where ϵ0 is the permittivity of free space and A is the area of the plates.
F=qE=q(qϵ0A)=q2ϵ0A
- The work done W by the external force when moving the plate from distance d to 2d is given by:
W=F⋅ddisplacement
- The displacement ddisplacement in this case is 2d−d=d.
W=F⋅d=(q2ϵ0A)⋅d
- Substituting the values, we get:
W=q2dϵ0A
The work done by the external force when one plate of a capacitor is moved from distance d to 2d is:
W=q2dϵ0A
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise155videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
The force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View Solution
Knowledge Check
- Question 1 - Select One
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
The separation between the plates of a charged parallel-plate capacitor is increased. The force between the plates
View SolutionIn the figure a capacitor of capacitance 2μF is connected to a cell of emf 20 volt. The plates of the capacitor are drawn apart slowly to double the distance between them. The work done by the external agent on the plates is:
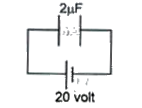 View Solution
View SolutionTwo parallel-plate capacitors with different distances between the plates are connected in parallel to a voltago source. A point positive charge is moved from a point 1 that is exactly in the middle between the plates of a capacitor Cl to a point 2 (or a capacitor C2) that lies at a distance from the negative plate of C2 equal to half the distance between the plates of Cl. Is any work done in the process?
View SolutionTwo similar parallel plate capacitors each of capaciti C0 are connected in series The combination is connected with a voltage source of V0. Now, seperation between the plates of one capacitor is increased by a distance d and the separation between the plates of another capacitor is decreased by the distance d2. The distance between the plates of each capacitor was d before the chane in sepration. Then select the correct choice.
View SolutionIn a parallel plate capacitor with plate area A and charge Q, the force on one plate because of the charge on the other is equal to
View SolutionA parallel plate capacitor is charged as shown (Q is given). A metal slab with the total charge +Q is placed inside the capacitor as shown. The thickness of the slab is d. The distance between the top plate and the top of the slab is 2d, and the distance between the bottom plate and the botthom of the slab is d. Each plate is grounded through a galvanometer as shown . Find the charge that passes through each galvanometer after both switches are closed simultaneously.
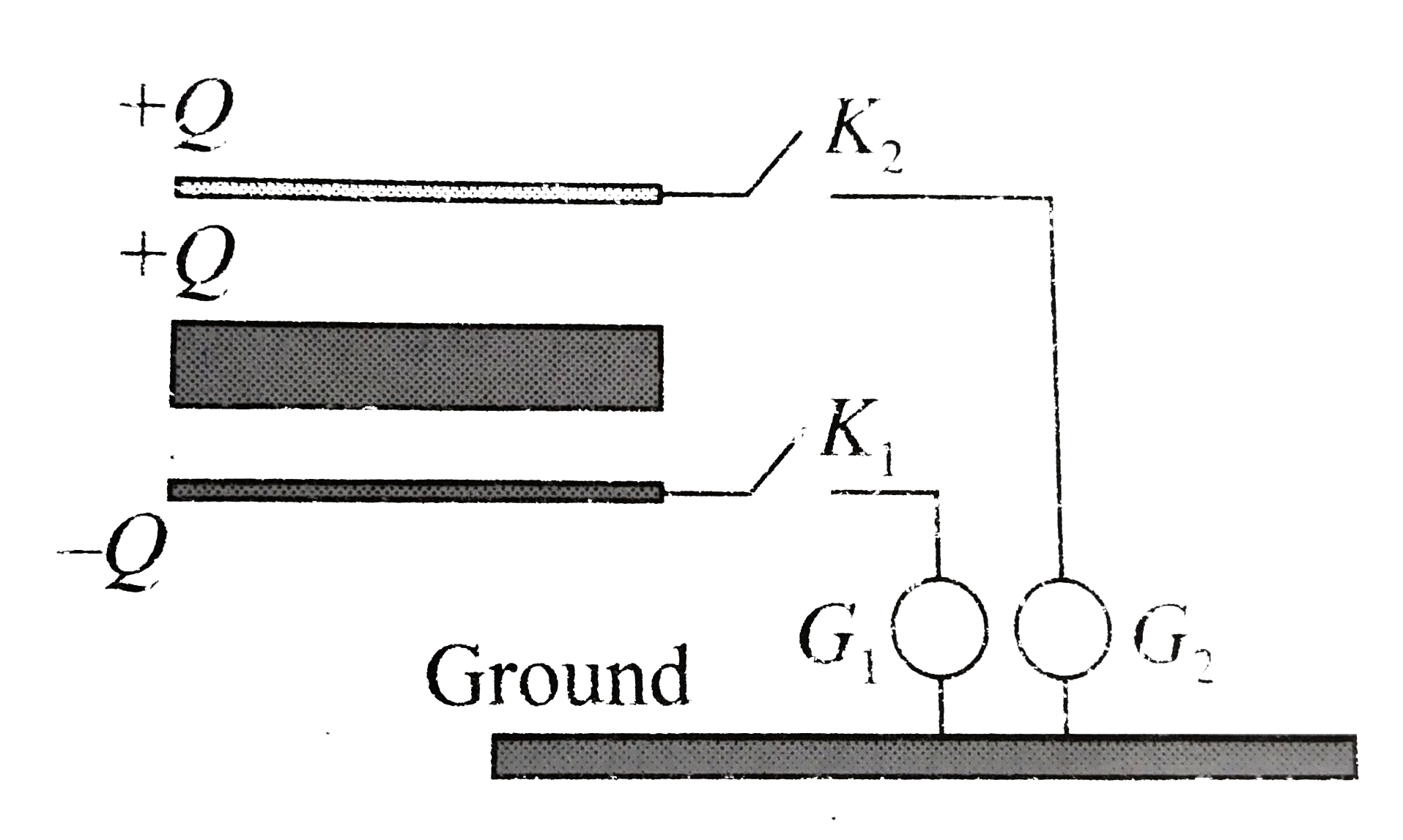 View Solution
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View Solution

