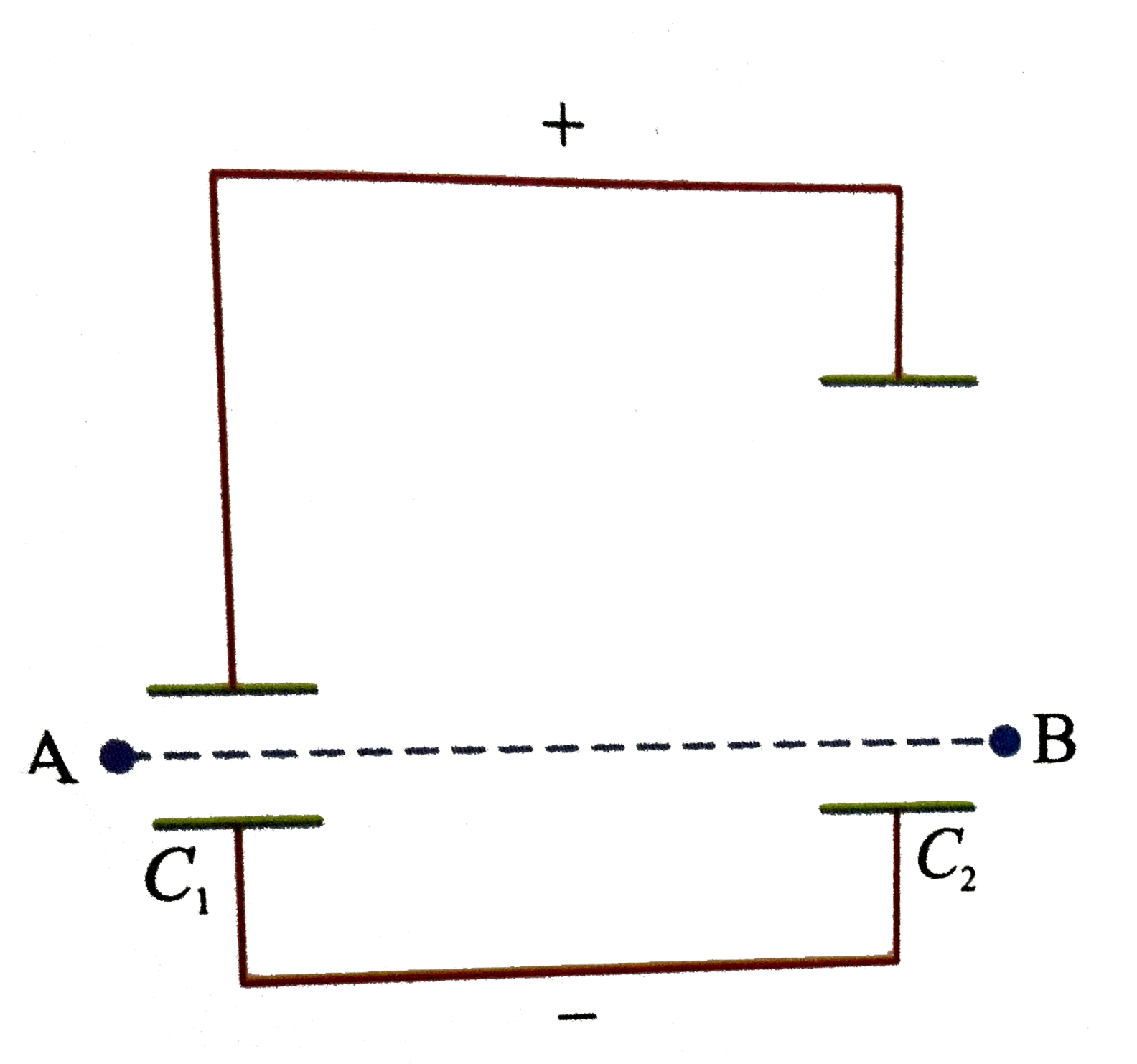
Two parallel-plate capacitors with different distances between the plates are connected in parallel to a voltago source. A point positive charge is moved from a point 1 that is exactly in the middle between the plates of a capacitor Cl to a point 2 (or a capacitor C2) that lies at a distance from the negative plate of C2 equal to half the distance between the plates of Cl. Is any work done in the process?
positive
negative
zero
data insufficient.
To determine whether any work is done when moving a positive charge from point 1 (midway between the plates of capacitor C1) to point 2 (near the negative plate of capacitor C2), we can follow these steps:
1. Identify the Configuration:
- We have two parallel plate capacitors, C1 and C2, connected in parallel to a voltage source.
- The distance between the plates of C1 is D, and the distance between the plates of C2 is different (let's denote it as D2).
2. Determine the Initial and Final Positions:
- Point 1 is located exactly in the middle of capacitor C1, which means it is at a distance of D/2 from either plate of C1.
- Point 2 is at a distance of D/2 from the negative plate of capacitor C2.
3. Calculate the Electric Potential:
- The electric potential (V) in a parallel plate capacitor is given by the formula:
V=E⋅d
where E is the electric field and d is the distance from the plate.
- For capacitor C1, the potential at point 1 (V1) is:
V1=E1⋅D2
- For capacitor C2, the potential at point 2 (V2) is:
V2=E2⋅D2
4. Analyze the Electric Fields:
- The electric field (E) between the plates of a capacitor is uniform and can be expressed as:
E=Vd
- Since both capacitors are connected to the same voltage source, the potential difference across each capacitor is the same. However, the distance between the plates may affect the electric field strength.
5. Compare the Potentials:
- Since point 1 is at the midpoint of C1 and point 2 is closer to the negative plate of C2, we can infer that:
V2>V1
- This is because the charge is moving from a region of lower potential (midway of C1) to a region of higher potential (closer to the negative plate of C2).
6. Calculate Work Done:
- The work done (W) in moving a charge (Q) in an electric field is given by:
W=Q(V2−V1)
- Since V2 > V1, it follows that:
W>0
- Therefore, the work done is positive.
Conclusion:
The work done in moving the positive charge from point 1 to point 2 is positive.
- We have two parallel plate capacitors, C1 and C2, connected in parallel to a voltage source.
- The distance between the plates of C1 is D, and the distance between the plates of C2 is different (let's denote it as D2).
- Point 1 is located exactly in the middle of capacitor C1, which means it is at a distance of D/2 from either plate of C1.
- Point 2 is at a distance of D/2 from the negative plate of capacitor C2.
- The electric potential (V) in a parallel plate capacitor is given by the formula:
V=E⋅d
where E is the electric field and d is the distance from the plate.
- For capacitor C1, the potential at point 1 (V1) is:
V1=E1⋅D2
- For capacitor C2, the potential at point 2 (V2) is:
V2=E2⋅D2
- The electric field (E) between the plates of a capacitor is uniform and can be expressed as:
E=Vd
- Since both capacitors are connected to the same voltage source, the potential difference across each capacitor is the same. However, the distance between the plates may affect the electric field strength.
- Since point 1 is at the midpoint of C1 and point 2 is closer to the negative plate of C2, we can infer that:
V2>V1
- This is because the charge is moving from a region of lower potential (midway of C1) to a region of higher potential (closer to the negative plate of C2).
- The work done (W) in moving a charge (Q) in an electric field is given by:
W=Q(V2−V1)
- Since V2 > V1, it follows that:
W>0
- Therefore, the work done is positive.
The work done in moving the positive charge from point 1 to point 2 is positive.
Similar Questions
Two parallel-plate capacitors with different distances between the plates are connected in parallel to a voltage source. A point positive charge is moved from a point A, that is exactly in the middle between the plates of a capacitor C1 to a point B(or a capacitor C2 that lies at a distance from the negative plate of C2 equal to half the distance between the plates of C1) During this process of moving the charge.
 .
.
View SolutionTo reduce the capacitance of parallel plate capacitor, the space between the plate is
View Solution
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
A parallel plate capacitor is charged. If the plates are pulled apart
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionForce of attraction between the plates of a parallel plate capacitor is
View SolutionThe capacitance of a parallel plate capacitor is 12μF. If the distance between the plates is doubled and area is halved, then new capacitance will be
View SolutionA very thin plate of metal is placed exactly in the middle of the two plates of a parallel plate capacitor. What will be the effect on the capacitance of the system?
View SolutionIf a thin metal foil of same area is placed between the two plates of a parallel plate capacitor of capacitance C, then new capacitance will be
View SolutionA capacitor is given a charge q. The distance between the plates of the capacitor is d. One of the plates is fixed and the other plate is moved away from the other till the distance between them becomes 2d. Find the work done by the external force.
View Solution