A capacitor of capacity 2μF is charged to 100V. What is the heat generated when this capacitor is connected in parallel to an another capacitor of same capacity?
2.5mJ
5.0mJ
10mJ
4mJ
The correct Answer is:B
To solve the problem of finding the heat generated when a charged capacitor is connected in parallel to another identical capacitor, we can follow these steps:
1. Calculate the Initial Charge on the Capacitor:
The charge Q on a capacitor is given by the formula:
Q=C×V
Where:
- C=2μF=2×10−6F
- V=100V
Substituting the values:
Q=2×10−6F×100V=2×10−4C=200μC
2. Determine the Final Charge on Each Capacitor:
When the charged capacitor is connected in parallel to another identical capacitor, the total charge will redistribute equally between the two capacitors. Thus, each capacitor will have:
Q1=Q2=Q2=200μC2=100μC
3. Calculate the Initial Potential Energy:
The initial potential energy Ui stored in the first capacitor can be calculated using the formula:
Ui=12CV2
Substituting the values:
Ui=12×2×10−6F×(100V)2=12×2×10−6×10000=10×10−3J=0.01J
4. Calculate the Final Potential Energy:
After connecting the two capacitors in parallel, the total capacitance becomes:
Ctotal=C1+C2=2μF+2μF=4μF
The final voltage Vf across the capacitors can be calculated using the total charge and total capacitance:
Vf=QCtotal=200μC4μF=50V
Now, we can calculate the final potential energy Uf:
Uf=12CtotalV2f=12×4×10−6F×(50V)2=12×4×10−6×2500=5×10−3J=0.005J
5. Calculate the Heat Generated:
The heat generated Qheat when the capacitors are connected is the difference between the initial and final potential energies:
Qheat=Ui−Uf=0.01J−0.005J=0.005J
Converting to millijoules:
Qheat=0.005J×1000=5mJ
Final Answer:
The heat generated when the capacitor is connected in parallel to another capacitor of the same capacity is 5 mJ.
The charge Q on a capacitor is given by the formula:
Q=C×V
Where:
- C=2μF=2×10−6F
- V=100V
Q=2×10−6F×100V=2×10−4C=200μC
When the charged capacitor is connected in parallel to another identical capacitor, the total charge will redistribute equally between the two capacitors. Thus, each capacitor will have:
Q1=Q2=Q2=200μC2=100μC
The initial potential energy Ui stored in the first capacitor can be calculated using the formula:
Ui=12CV2
Substituting the values:
Ui=12×2×10−6F×(100V)2=12×2×10−6×10000=10×10−3J=0.01J
After connecting the two capacitors in parallel, the total capacitance becomes:
Ctotal=C1+C2=2μF+2μF=4μF
The final voltage Vf across the capacitors can be calculated using the total charge and total capacitance:
Vf=QCtotal=200μC4μF=50V
Now, we can calculate the final potential energy Uf:
Uf=12CtotalV2f=12×4×10−6F×(50V)2=12×4×10−6×2500=5×10−3J=0.005J
The heat generated Qheat when the capacitors are connected is the difference between the initial and final potential energies:
Qheat=Ui−Uf=0.01J−0.005J=0.005J
Converting to millijoules:
Qheat=0.005J×1000=5mJ
The heat generated when the capacitor is connected in parallel to another capacitor of the same capacity is 5 mJ.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
A capacitor of capacity 20microF is charged upto 500V and and disconnected from cell. Now this charged capacitor is connected to another capacitor of capacitance C If final common potential is 20V then find the capacitance C.
View SolutionA 100μF capacitor is charged to 100V. After the charging, battery is disconnected. The capacitor is then connected in parallel to another capacitor. The final voltage is 20V. Calculate the capacity of second capacitor.
View Solution
Knowledge Check
In a parallel plate capacitor , the capacity increases if
Aarea of the plate is decreasedBdistance between the plates increasesCarea of the plate is increasedDdielectric constant decreases.
A capacitor of capacity C1=1μF is charged to a potential of 100 V. The charging battery is then removed and it is connected to another capacitor of capacity C2=2μF. One plate of C2 is earthed as shown in figure. The charges on C1andC2 in steady state will be

View SolutionA capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA 8uF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
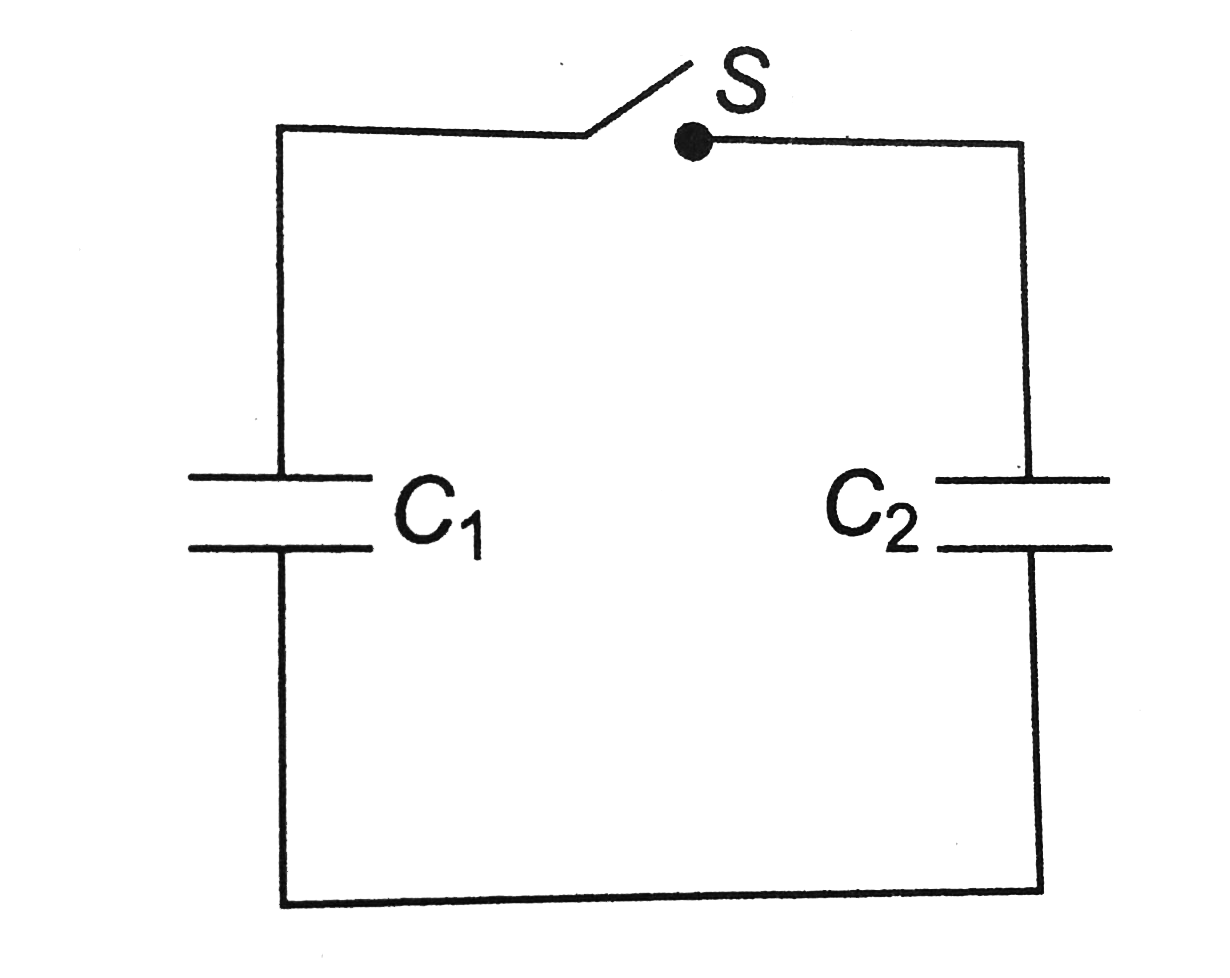
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
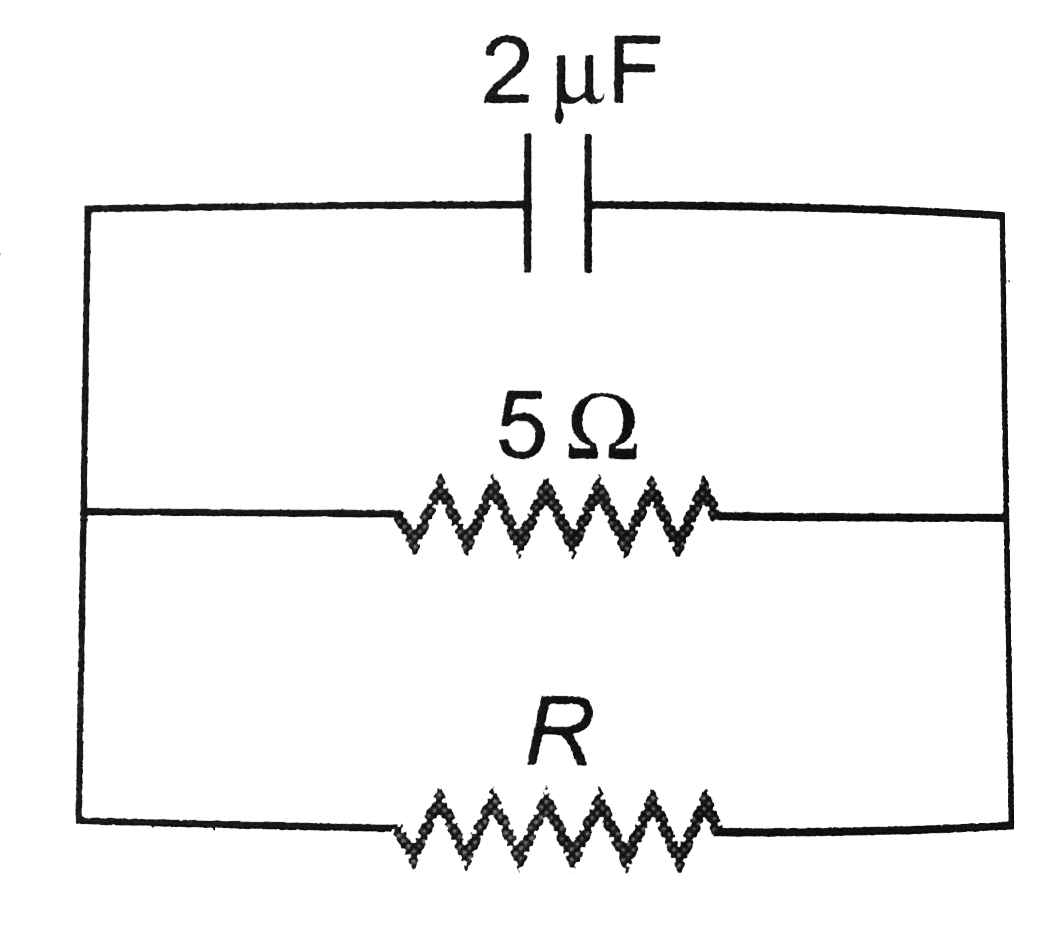
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to

View SolutionA capacitor having capacity of 2μF is charged to 200V and then the plates of the capacitor are connected to a resistance wire. The heat produced in joule will be
View SolutionA capacitor C is fully charged with voltage V0. After disconnecting the voltage source, it is connected in parallel with another uncharged capacitor of capacitance C2. The energy loss in the process after the charge is distributed between the two capacitors is :
View Solution
