An infinite sheet of charge has a surfaces charge density of 10−7Cm2. The separation between two equipotential surfce whose potentials differ by 5V is
0.64cm
0.88mm
0.32cm
5×10−7m
The correct Answer is:B
To solve the problem, we need to find the separation between two equipotential surfaces given the surface charge density and the potential difference. Here's the step-by-step solution:
Step 1: Understand the Electric Field due to an Infinite Sheet of Charge
The electric field (E) due to an infinite sheet of charge with surface charge density (σ) is given by the formula:
E=σ2ϵ0
where:
- σ=10−7C/m2 (surface charge density)
- ϵ0=8.85×10−12C2/(N⋅m2) (permittivity of free space)
Step 2: Calculate the Electric Field
Substituting the value of σ into the formula:
E=10−72×8.85×10−12
Calculating this gives:
E=10−71.77×10−11≈5.64×103N/C
Step 3: Relate Electric Field to Potential Difference and Distance
The relationship between electric field (E), potential difference (V), and distance (d) is given by:
V=E⋅d
In this case, we know the potential difference (V) is 5 V. Therefore, we can rearrange the equation to find the distance (d):
d=VE
Step 4: Substitute the Values
Substituting the values of V and E into the equation:
d=5V5.64×103N/C
Step 5: Calculate the Distance
Calculating this gives:
d≈55.64×103≈8.86×10−4m
Converting this to millimeters:
d≈0.886mm
Final Answer
The separation between the two equipotential surfaces is approximately:
d≈0.886mm
The electric field (E) due to an infinite sheet of charge with surface charge density (σ) is given by the formula:
E=σ2ϵ0
where:
- σ=10−7C/m2 (surface charge density)
- ϵ0=8.85×10−12C2/(N⋅m2) (permittivity of free space)
Substituting the value of σ into the formula:
E=10−72×8.85×10−12
Calculating this gives:
E=10−71.77×10−11≈5.64×103N/C
The relationship between electric field (E), potential difference (V), and distance (d) is given by:
V=E⋅d
In this case, we know the potential difference (V) is 5 V. Therefore, we can rearrange the equation to find the distance (d):
d=VE
Substituting the values of V and E into the equation:
d=5V5.64×103N/C
Calculating this gives:
d≈55.64×103≈8.86×10−4m
Converting this to millimeters:
d≈0.886mm
The separation between the two equipotential surfaces is approximately:
d≈0.886mm
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
An infinite nonconducting sheet of charge has a surface charge density of 107C/m2. The separation between two equipotential surfaces near the whose potential differ by 5V is
View SolutionAn infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
View Solution
Knowledge Check
- Question 1 - Select One
An infinite cylinder of radius ro, carrying linear charge density λ. The equation of the equipotential surface for the cylinder is
Ar=r0eπε0[V(r)+V(r0)]λBr=r0e2πε0[V(r)−V(r0)]λ2Cr=r0e−2πε0[V(r)=V(r0)]λDr=r0e−2πε0[V(r)−V(r0)]λ
An infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
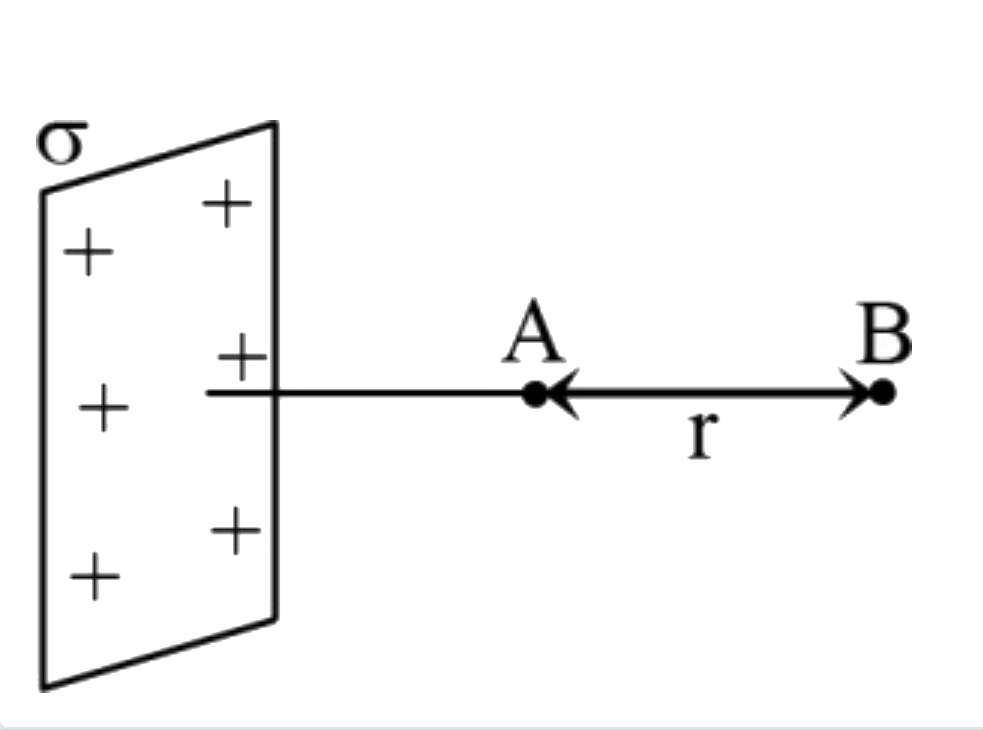 View Solution
View SolutionElectric field intensity at a point due to an infinite sheet of charge having surface charge density σ is E.If sheet were conducting electric intensity would be
View SolutionTwo charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionWhen the separation between two charges is increase the electric potential energy of the charges.
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
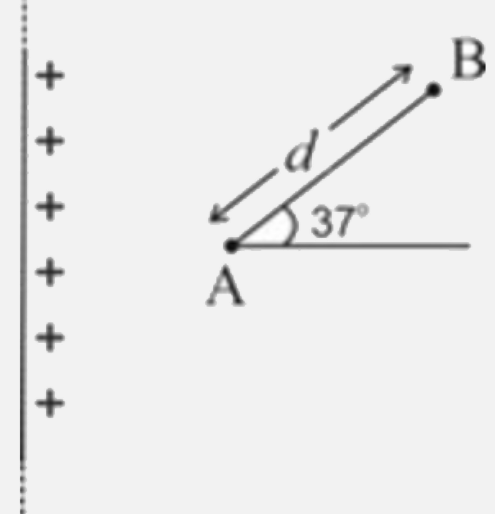 View Solution
View Solution

