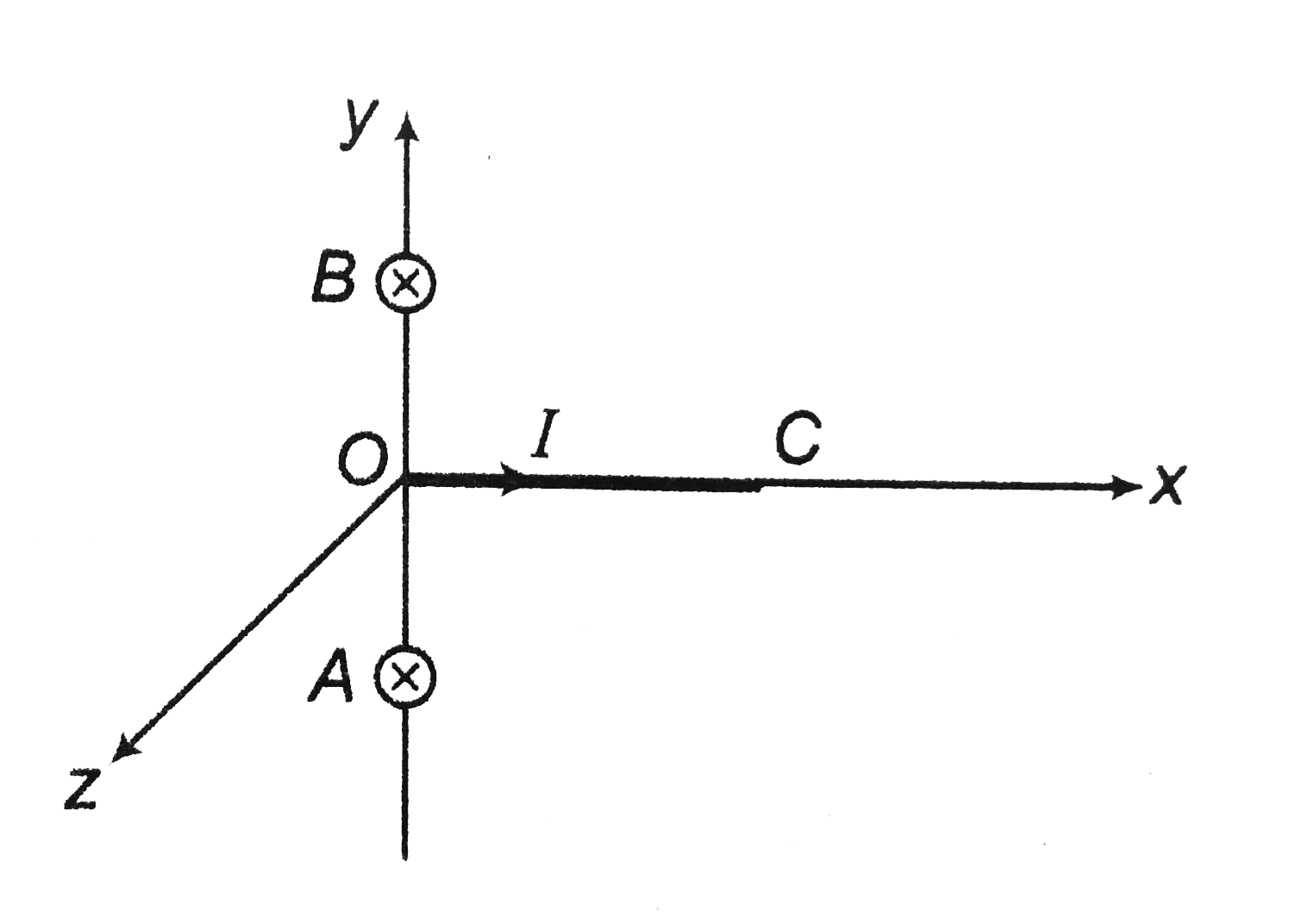
A straight segment OC (of lengh L) of a circuit carrying a current I is placed along the x-axis. Two infinitely long straight wire A and B each extending from z=−∞→+∞ are fixed at y=−a and y=+a respectively as show in the figure. If the wires A and B each carry a current I into the plane of the paper, obtain the expression for the force acting on the segment OC. What will be the force on OC if the current in the wire B is reversed?
a. Let us assume a segment of wire OC at a point P, a distance x from the centre d length dx as shown in figure.
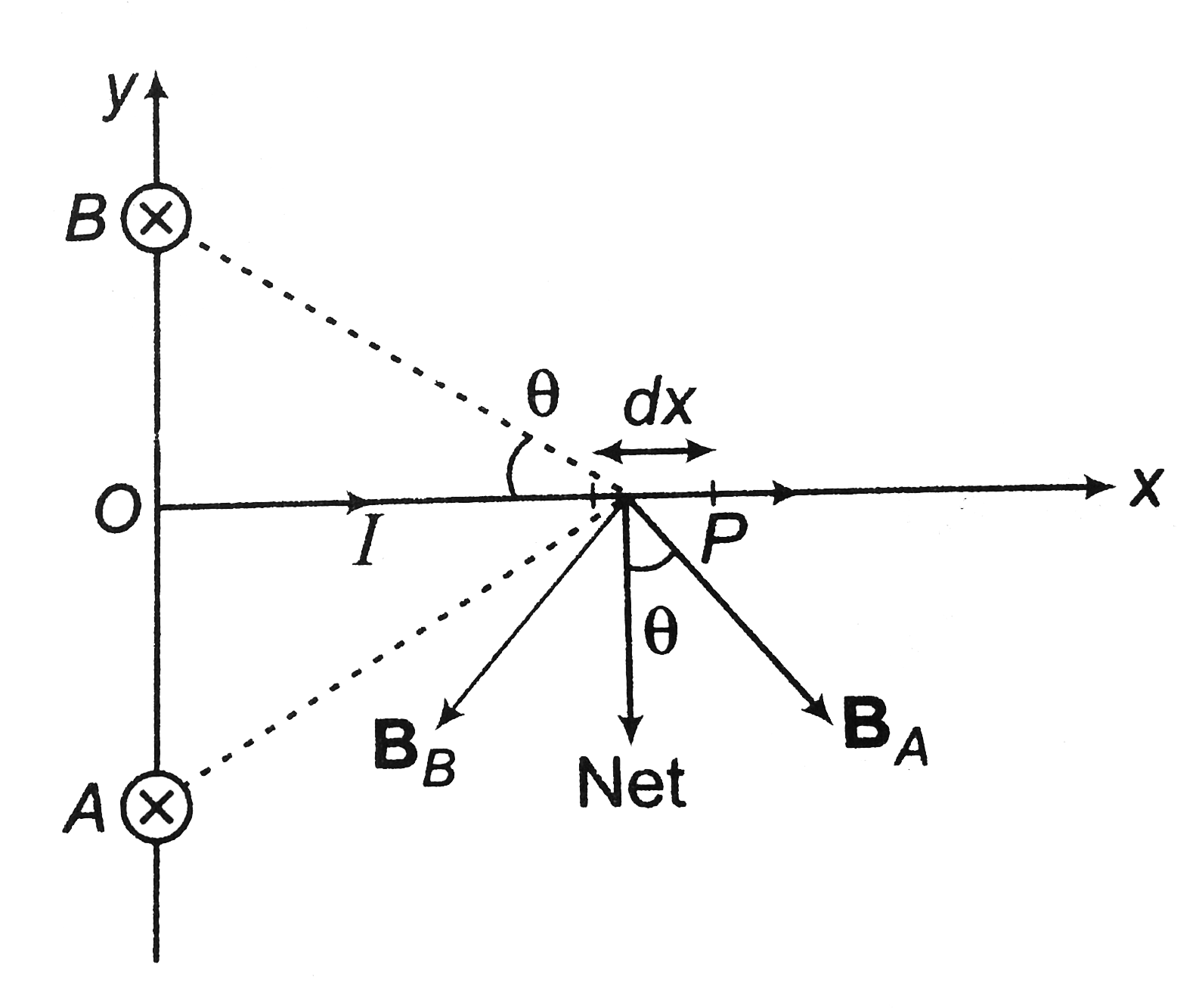
Magnetic field at P due to current in wires A and B will be in the directions perpendicular to AP and BP respectively as shown.
|B|=μ2πIAP
therefore, net magnetic force at P will be along negative y-axis as shown below
Bnet=2|B|cosθ
=2(μ02π)IAP(xAP)
Bnet=(μ0π)=Ix(AP)2
Bnet=μπIx(a2+x2)

Therefore, force on this element will be
dF=I{μ0πIxa2+x2}dx [in negative z-direction]
∴ total force on the wire will be
F=∫x=Lx=0 dFμ0I2π∫L0xdxx2+a2
=μ0I22πln(L2+a2)a2 [in negative z-axis]
Hence, F=−μ0I22πln(L2+a2a2)ˆk
b. When direction of current in B is reversed net magnetic field is a along the current. Hence force is zero
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A straight segment OC(of length L meter) of a circuit carrying a current Iamp is placed along the x- axis ( fig.). Two infinetely long straight wires AandB , each extending from z=−∞→+∞, are fixed at y = -a meter and y = +a meter respectively, as shown in the figure.
If the wires AandB each carry a current Iamp into the plane of the paper, obtain the expression for the force acting on the segment OC. What will be the force on OC if the current in the wire B is reversed?
View SolutionA straight wire carrying current is parallel to the y-axis as shown in Fig. The
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionIn the figure PQ is a long current carrying wire which is placed near a current carrying coil. The direction of the force acting on PQ will be

View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
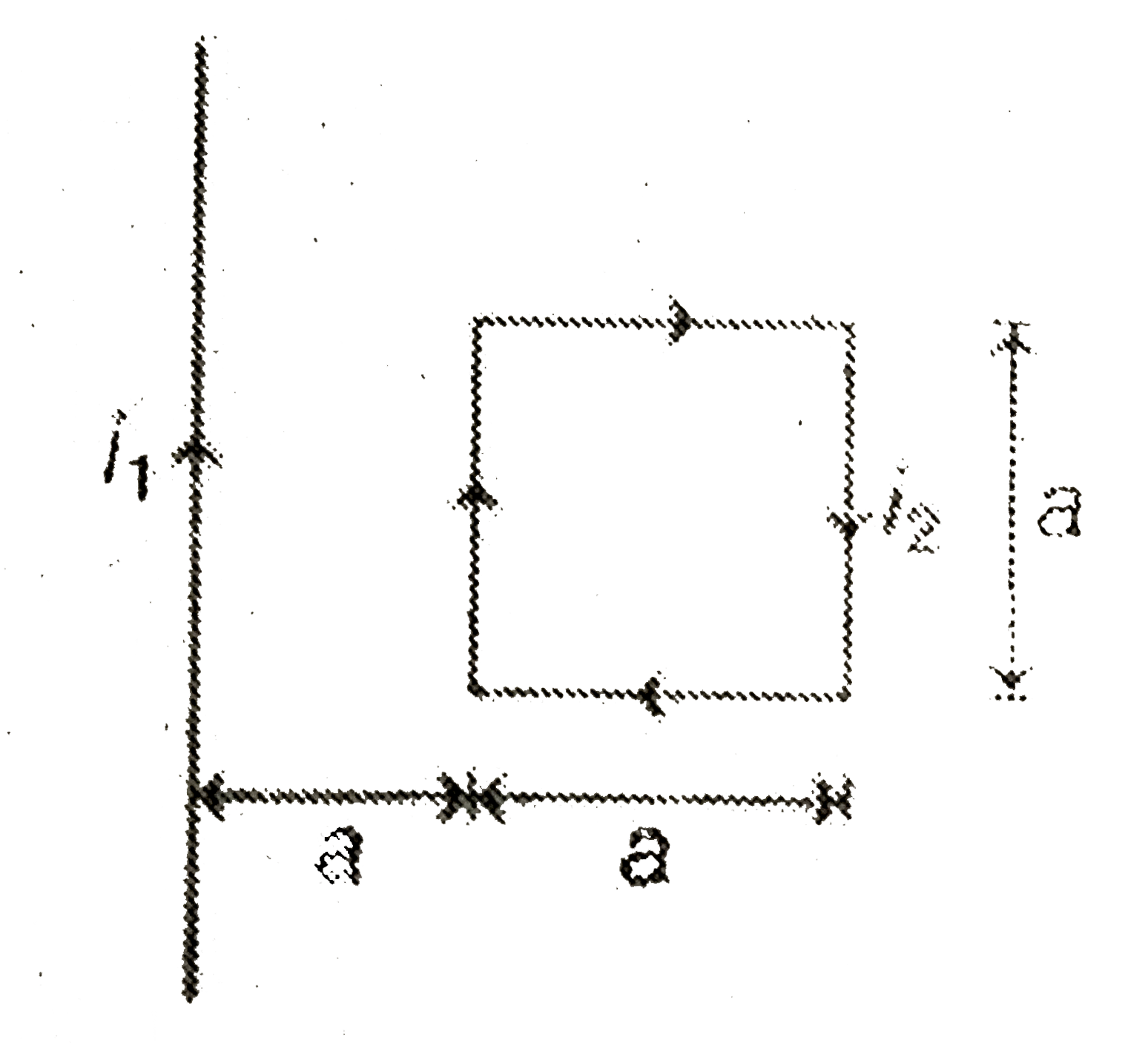
View SolutionA square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.

View SolutionTwo straight infinitely long current carrying wires are kept along Z-axis at the coordinates (0,a,0) and (0, -a, 0) respectively, as shown in the figure. The current in each of the wire is equal and along negative Z-axis (into the plane of the paper).
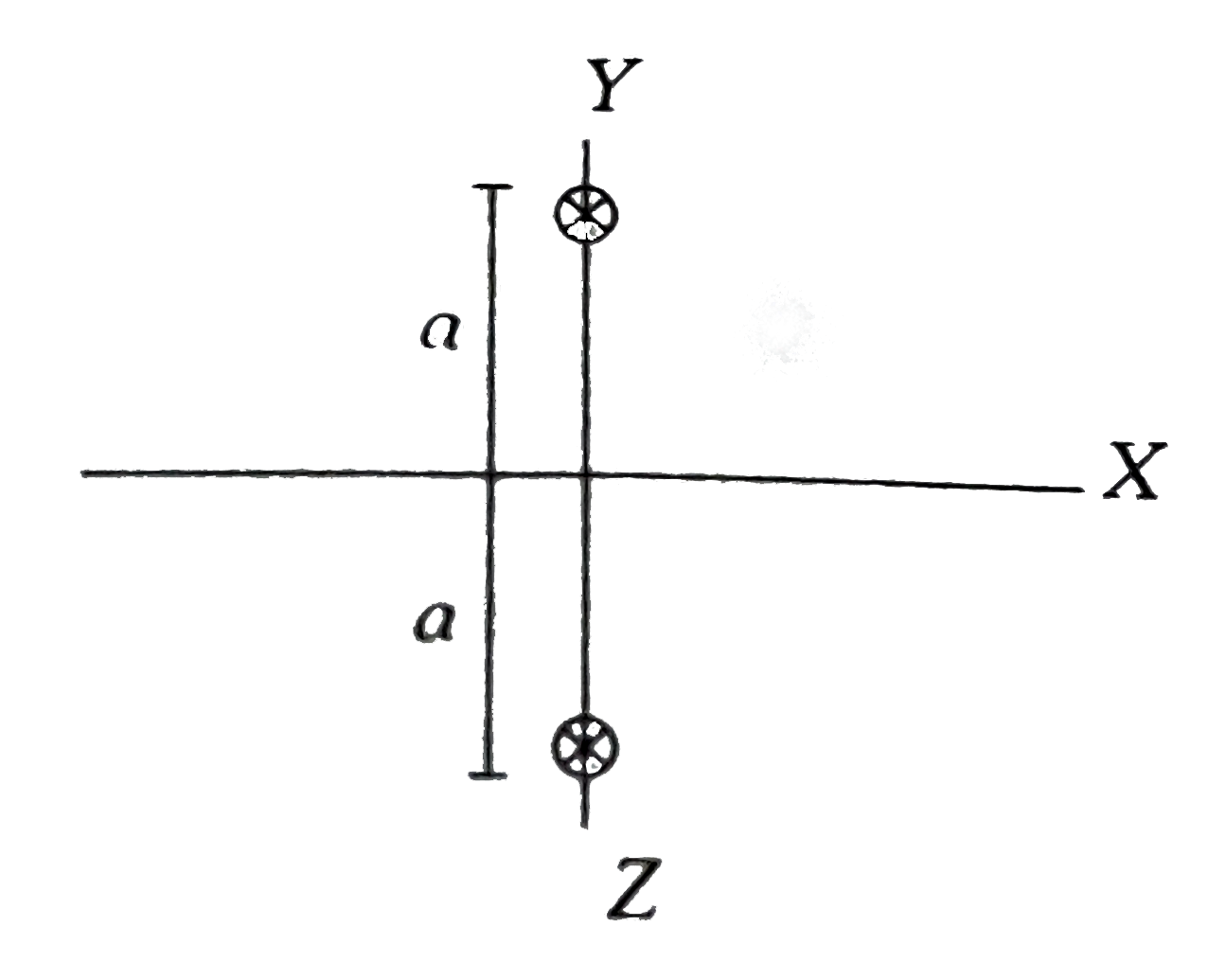
The variation of magnetic field on the X-axis will be approximately
View SolutionA long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
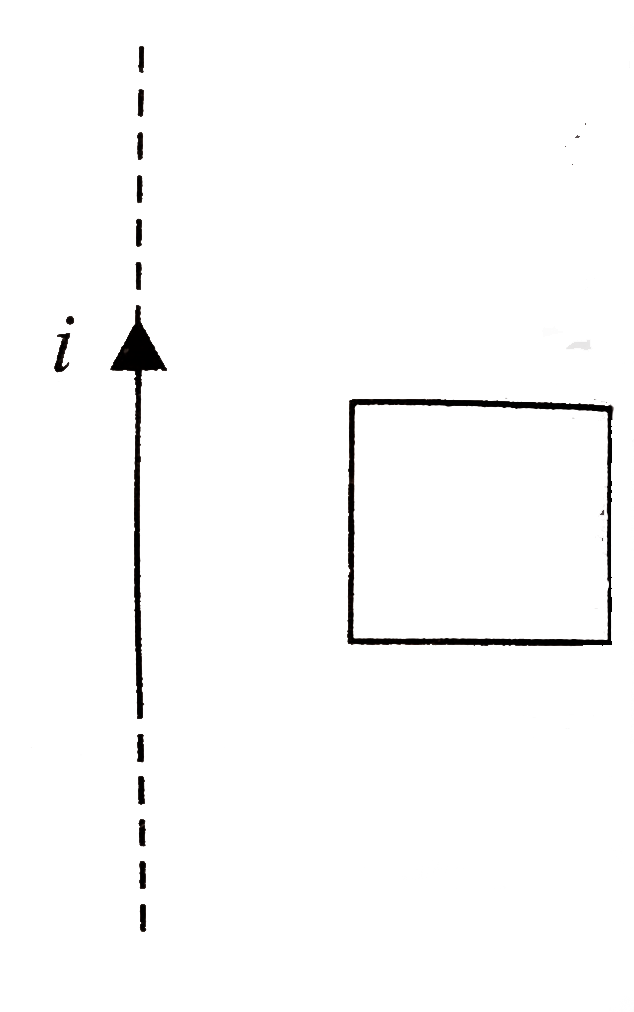
View SolutionA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
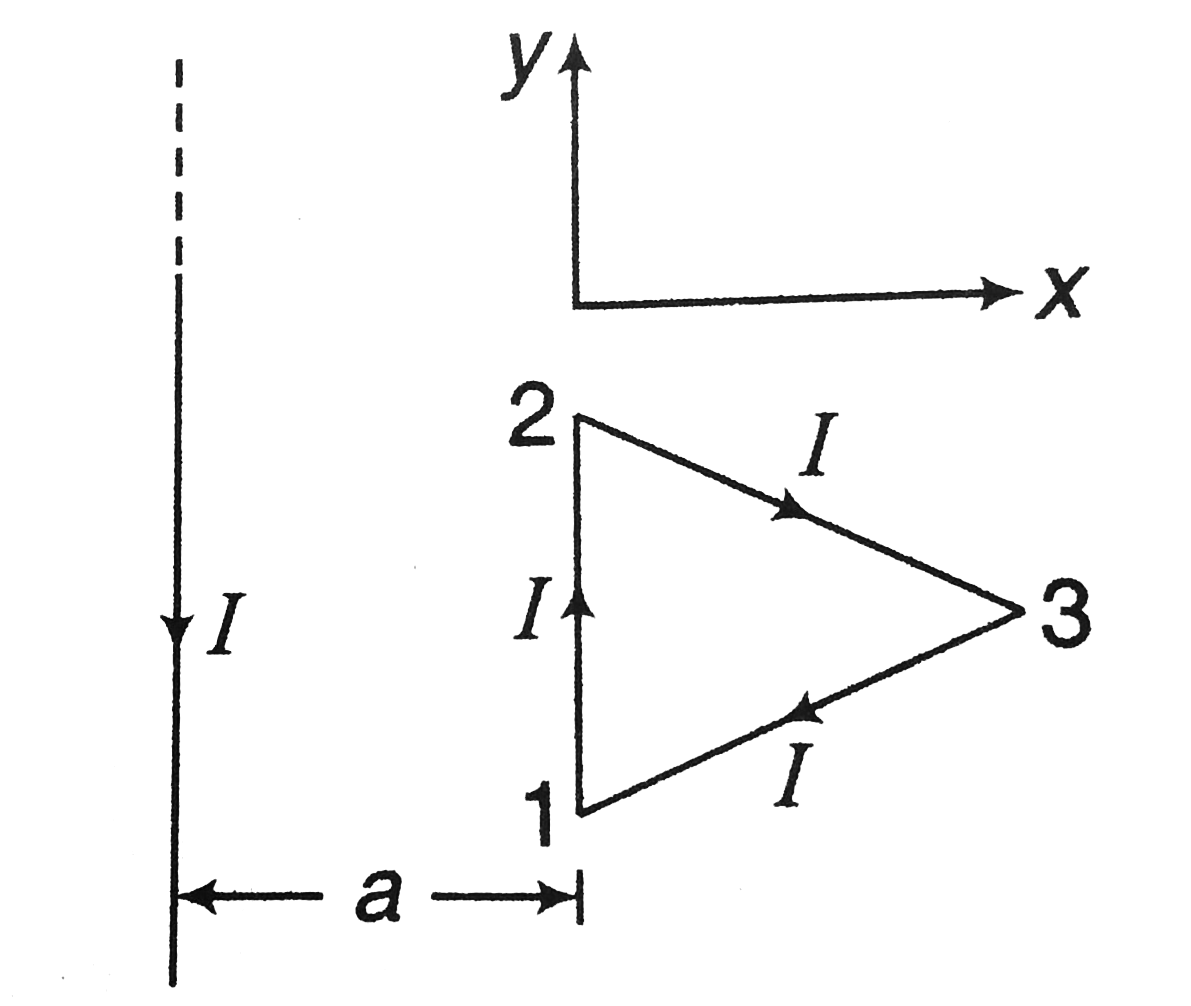
View SolutionAn equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.
View Solution
