A long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
the magnetic fields are equal
the directions of the magnetic fields are the same
the magnitudes of the magnetic fields are equal
the field at one point is opposite to that at the other point.
The correct Answer is:B, C, D
To solve the problem, we need to analyze the magnetic field produced by a long straight wire carrying a current along the z-axis. The magnetic field at any point in the x-y plane due to this wire can be calculated using the formula:
B=μ0I2πd
where:
- B is the magnetic field,
- μ0 is the permeability of free space,
- I is the current flowing through the wire,
- d is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
1. Identify the Wire and Points:
- The wire is oriented along the z-axis.
- We need to find two points in the x-y plane where the magnetic fields can be compared.
2. Magnetic Field Calculation:
- For a point at distance d1 from the wire, the magnetic field B1 is given by:
B1=μ0I2πd1
- For another point at distance d2 from the wire, the magnetic field B2 is given by:
B2=μ0I2πd2
3. Direction of the Magnetic Field:
- Using the right-hand rule, the direction of the magnetic field will depend on the position of the points relative to the wire.
- If one point is above the wire and the other is below, the magnetic fields at these points will be in opposite directions.
4. Magnitude of the Magnetic Fields:
- If d1=d2, then B1=B2.
- If d1≠d2, the magnitudes will differ, but we can find points where the magnitudes are equal by setting d1=d and d2=−d (i.e., symmetrical points).
5. Conclusion:
- The magnetic fields at the two points can be equal in magnitude but opposite in direction if they are equidistant from the wire on opposite sides.
- Therefore, the correct options based on the analysis are:
- The magnitudes of the magnetic fields are equal.
- The directions of the magnetic fields are opposite.
Final Answer:
- The correct options are:
- C: The magnitudes of the magnetic fields are equal.
- D: The field at one point is opposite to that at the other point.
- B is the magnetic field,
- μ0 is the permeability of free space,
- I is the current flowing through the wire,
- d is the perpendicular distance from the wire to the point where the magnetic field is being calculated.
- The wire is oriented along the z-axis.
- We need to find two points in the x-y plane where the magnetic fields can be compared.
- For a point at distance d1 from the wire, the magnetic field B1 is given by:
B1=μ0I2πd1
- For another point at distance d2 from the wire, the magnetic field B2 is given by:
B2=μ0I2πd2
- Using the right-hand rule, the direction of the magnetic field will depend on the position of the points relative to the wire.
- If one point is above the wire and the other is below, the magnetic fields at these points will be in opposite directions.
- If d1=d2, then B1=B2.
- If d1≠d2, the magnitudes will differ, but we can find points where the magnitudes are equal by setting d1=d and d2=−d (i.e., symmetrical points).
- The magnetic fields at the two points can be equal in magnitude but opposite in direction if they are equidistant from the wire on opposite sides.
- Therefore, the correct options based on the analysis are:
- The magnitudes of the magnetic fields are equal.
- The directions of the magnetic fields are opposite.
- The correct options are:
- C: The magnitudes of the magnetic fields are equal.
- D: The field at one point is opposite to that at the other point.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A straight wire carrying current is parallel to the y-axis as shown in Fig. The
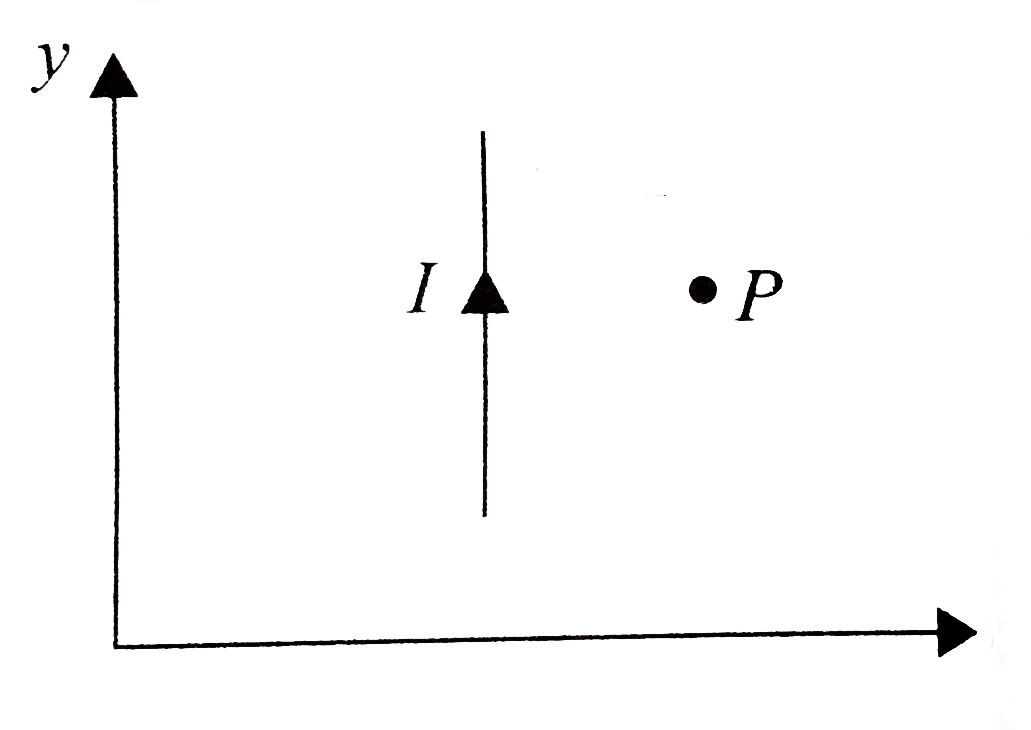
View SolutionFour very long straight wires carry equal electric currents in the +z direction. They intersect the xy plane at (x,y)=(−a,0),(0,a),(a,0), and (0,−a). The magnetic force exerted on the wire at position (−a,0) is along
View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5TA rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current I is established in the wire as shown in the figure ,
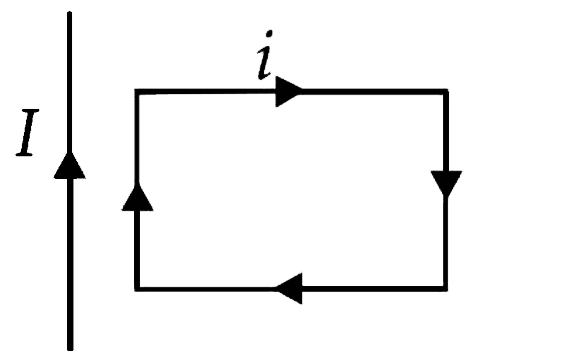 Arotate about an axis parallel to the wireBmove away from the wireCmove towards the wireDremain stationary
Arotate about an axis parallel to the wireBmove away from the wireCmove towards the wireDremain stationary
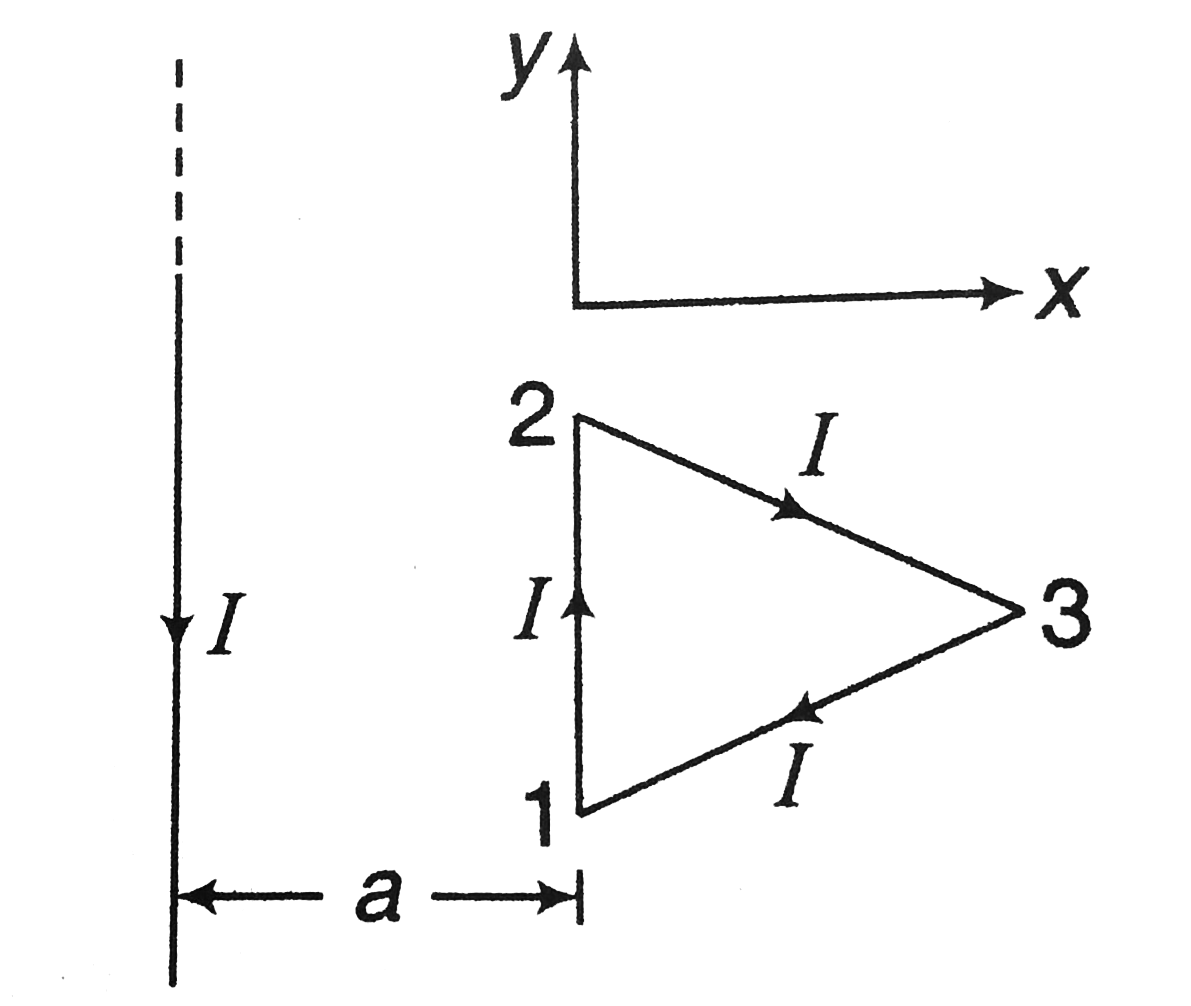
An equilateral triangular frame with side a carrying a current I is placed at a distance a from an infinitely long straight wire carrying a current I as shown in the figure. One side of the frame isparallel to the wire. The whole system lies in the xy-plane. Find the magnetic force F acting on the frame.
View SolutionA long straight wire carries a current of 35A. What is the magnitude of the field →B at a point 20cm from the wire?
View SolutionA long straight wire carries a current I0, at distance a and b=3a from it there are two other wires, parallel to the former one, which are interconnected by a resistance R(figure).A connector slides without friction along the wires with a constant velocity v.Assuming the resistance of the wires,the connector, the sliding contacts and the self-inductance of the frame to be negligible. The point of application (distance from the long wire) of magnetic force on sliding wire due to the long wire is 2alnx from long wire.Then find out value of x.

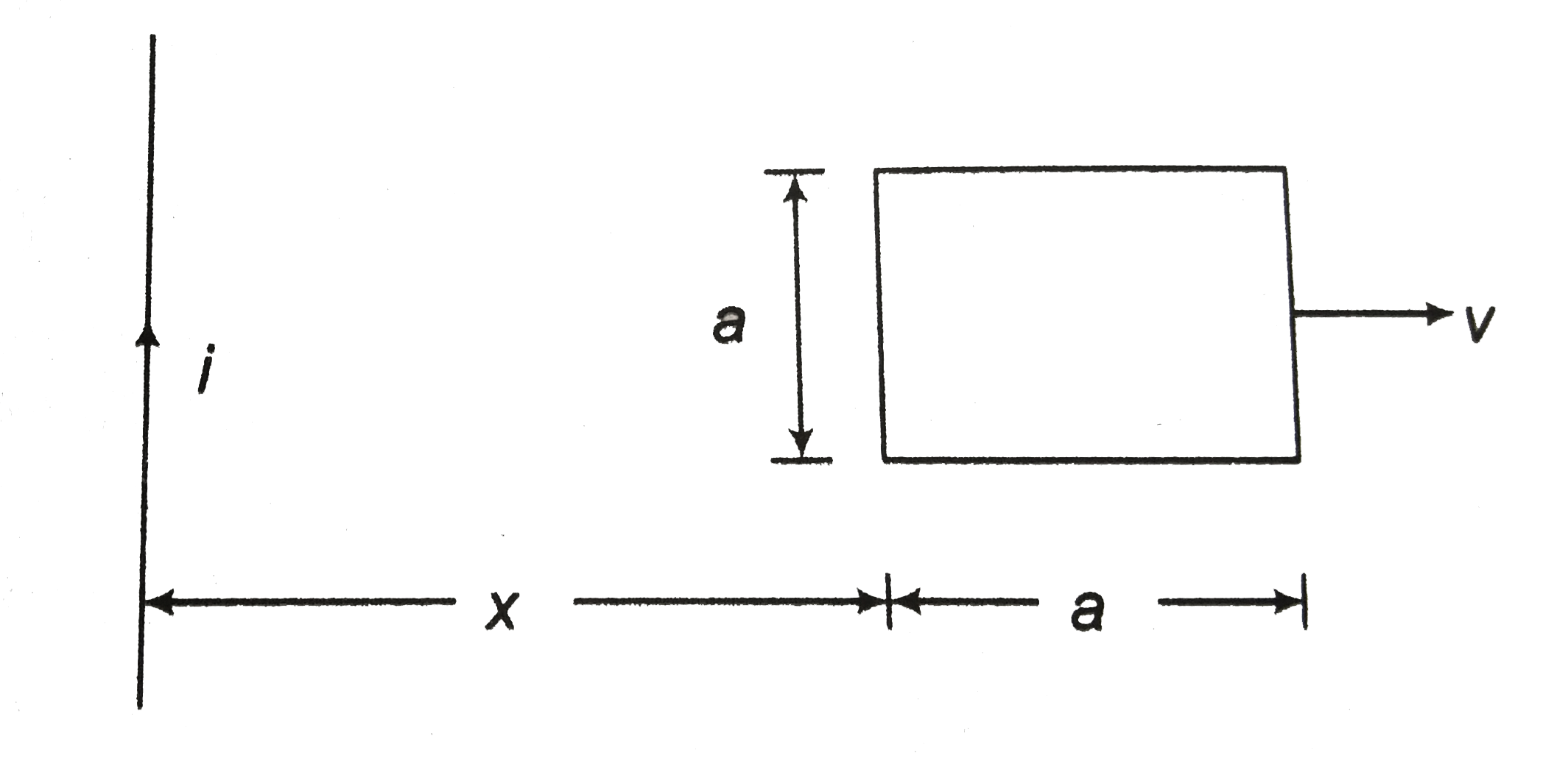
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
View SolutionA long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
View SolutionThe figure shows a long straigh wire carryhing a current I1 along the axis of a circular ring carrying a current I_2. Identify the correct statement.

View Solution
