When E↑↑Be and particle velocity is perpendicuular to both of these field.
To solve the problem, we need to analyze the motion of a charged particle in the presence of both electric and magnetic fields when the velocity of the particle is perpendicular to both fields. Let's break this down step by step.
Step 1: Understanding the Setup
We have:
- An electric field E in the y-direction.
- A magnetic field B in the x-direction.
- The velocity v of the particle is perpendicular to both E and B.
Step 2: Forces Acting on the Particle
The forces acting on the particle are:
1. Electric Force: FE=qE
2. Magnetic Force: FB=q(v×B)
Step 3: Writing the Equations of Motion
The total force F on the particle can be expressed as:
F=FE+FB
Substituting the expressions for the forces:
F=qE+q(v×B)
Step 4: Analyzing the Motion
Given that v is perpendicular to both E and B:
- The electric force will act in the y-direction.
- The magnetic force will act in the z-direction (since v is in the y-direction and B is in the x-direction).
Step 5: Finding the Acceleration
The acceleration a can be found using Newton's second law:
a=Fm=qEm+q(v×B)m
Substituting the known forces:
a=qEm^j+qvBm^k
Step 6: Writing the Velocity Components
The velocity of the particle can be expressed in terms of its components:
v=vx^i+vy^j+vz^k
Where vx is constant (due to the absence of force in the x-direction), vy will change due to the electric field, and vz will change due to the magnetic field.
Step 7: Finding the Trajectory
To find the trajectory, we can integrate the acceleration to find the velocity and then integrate the velocity to find the position. The equations will yield a helical path due to the combined effects of the electric and magnetic fields.
Step 8: Final Position Vector
The final position vector R(t) can be expressed as:
R(t)=Rx(t)^i+Ry(t)^j+Rz(t)^k
Where:
- Rx(t) is determined by the constant velocity in the x-direction.
- Ry(t) is influenced by the electric field.
- Rz(t) is influenced by the magnetic field.
Final Equation
The final trajectory can be expressed as:
R(t)=(v0⋅t)^i+(12qEmt2)^j+(R⋅(1−cos(qBtm)))^k
We have:
- An electric field E in the y-direction.
- A magnetic field B in the x-direction.
- The velocity v of the particle is perpendicular to both E and B.
The forces acting on the particle are:
1. Electric Force: FE=qE
2. Magnetic Force: FB=q(v×B)
The total force F on the particle can be expressed as:
F=FE+FB
Substituting the expressions for the forces:
F=qE+q(v×B)
Given that v is perpendicular to both E and B:
- The electric force will act in the y-direction.
- The magnetic force will act in the z-direction (since v is in the y-direction and B is in the x-direction).
The acceleration a can be found using Newton's second law:
a=Fm=qEm+q(v×B)m
Substituting the known forces:
a=qEm^j+qvBm^k
The velocity of the particle can be expressed in terms of its components:
v=vx^i+vy^j+vz^k
Where vx is constant (due to the absence of force in the x-direction), vy will change due to the electric field, and vz will change due to the magnetic field.
To find the trajectory, we can integrate the acceleration to find the velocity and then integrate the velocity to find the position. The equations will yield a helical path due to the combined effects of the electric and magnetic fields.
The final position vector R(t) can be expressed as:
R(t)=Rx(t)^i+Ry(t)^j+Rz(t)^k
Where:
- Rx(t) is determined by the constant velocity in the x-direction.
- Ry(t) is influenced by the electric field.
- Rz(t) is influenced by the magnetic field.
The final trajectory can be expressed as:
R(t)=(v0⋅t)^i+(12qEmt2)^j+(R⋅(1−cos(qBtm)))^k
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
Assertion When a charged particle moves perpendicular to a uniform magnetic field then its momentum remains constant.
Reason Magnetic force acts perpendicular to the velocity of the particle.View SolutionAn (α)-particle and a proton are both simultaneously projected in opposite direction into a region of constant magnetic field perpendicular to the direction of the field. After some time it is found that the velocity of the (α)-particle has changed in a direction by 45∘. Then at this time, the angle between velocity vectors of (α)-particle and proton is
View SolutionAn (α)-particle and a proton are both simultaneously projected in opposite direction into a region of constant magnetic field perpendicular to the direction of the field. After some time it is found that the velocity of the (α)-particle has changed in a direction by 45∘. Then at this time, the angle between velocity vectors of (α)-particle and proton is
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
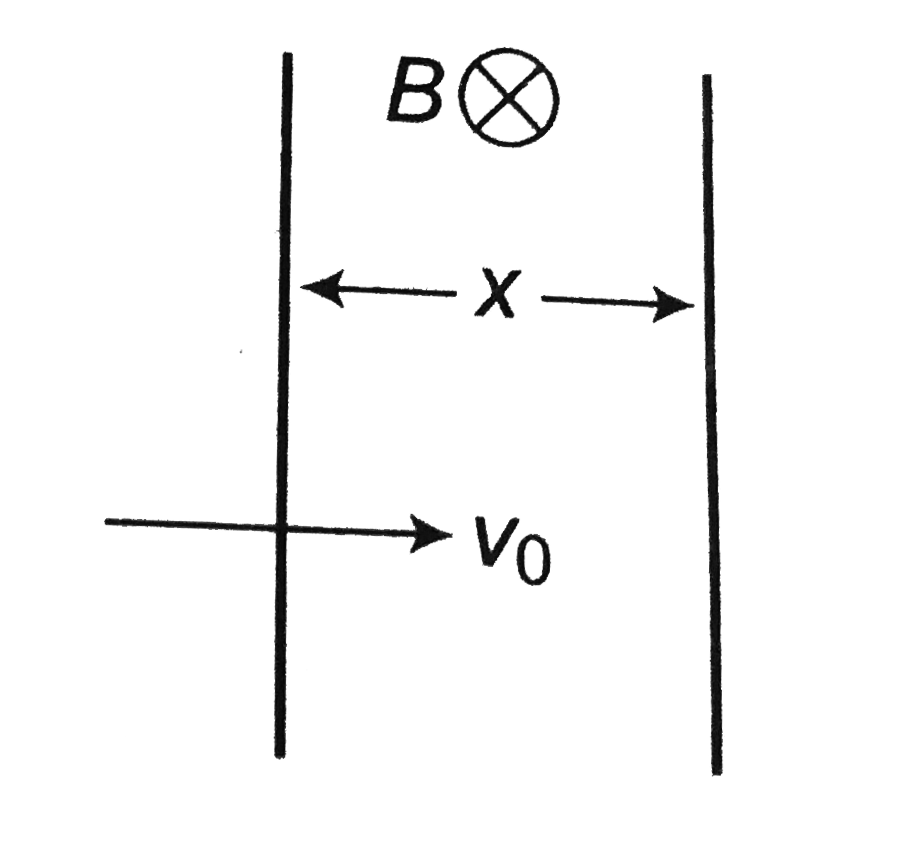 View Solution
View SolutionA charged particle enters a uniform magnetic field with velocity v0=4m/s perpendicular to it, the length of magnetic field is x=(√32)R, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.
View SolutionWhen a charged particle moving with velocity →v is subjected to a magnetic field of induction →B, the force on it is non-zero. This implies that:
View SolutionA particle moves in a region having a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
View SolutionWhich of the following particles will describe the smallest circle when projected with the same velocity perpendicular to a magnetic field?
View SolutionWhich of the follwing particles will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field?
View SolutionWhich of the follwing particles will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field?
View Solution

