A square loop of side a carris a current I. The magnetic field at the centre of the loop is
2μ0I√2πa
μ0I√2πa
4μ0I√2πa
μ0Iπa
The correct Answer is:A
To find the magnetic field at the center of a square loop of side a carrying a current I, we can follow these steps:
Step 1: Understand the Geometry of the Square Loop
The square loop has four sides, and we will denote the corners of the square as A,B,C,D. The center of the square, where we want to find the magnetic field, is point P.
Step 2: Magnetic Field Contribution from Each Side
The magnetic field at the center due to each straight segment of the wire can be calculated using the Biot-Savart Law. For a straight current-carrying wire, the magnetic field B at a distance r from the wire is given by:
B=μ0I4πrsinθ
where θ is the angle between the wire and the line connecting the wire to the point where the field is being calculated.
Step 3: Determine the Distance and Angles
For each side of the square, the distance from the center P to the midpoint of each side is a2. The angle θ for each side is 45∘ since the current flows perpendicular to the line connecting the center to the midpoint of each side.
Step 4: Calculate the Magnetic Field from One Side
Using the formula for the magnetic field:
Bone side=μ0I4π(a2)sin(45∘)
Since sin(45∘)=1√2, we can substitute this into the equation:
Bone side=μ0I4π(a2)⋅1√2=μ0I2πa⋅1√2
Step 5: Total Magnetic Field from All Four Sides
Since all four sides contribute equally to the magnetic field at the center, we multiply the contribution from one side by 4:
Btotal=4⋅Bone side=4⋅μ0I2πa⋅1√2=2√2μ0Iπa
Final Result
Thus, the magnetic field at the center of the square loop is given by:
B=2√2μ0Iπa
The square loop has four sides, and we will denote the corners of the square as A,B,C,D. The center of the square, where we want to find the magnetic field, is point P.
The magnetic field at the center due to each straight segment of the wire can be calculated using the Biot-Savart Law. For a straight current-carrying wire, the magnetic field B at a distance r from the wire is given by:
B=μ0I4πrsinθ
where θ is the angle between the wire and the line connecting the wire to the point where the field is being calculated.
For each side of the square, the distance from the center P to the midpoint of each side is a2. The angle θ for each side is 45∘ since the current flows perpendicular to the line connecting the center to the midpoint of each side.
Using the formula for the magnetic field:
Bone side=μ0I4π(a2)sin(45∘)
Since sin(45∘)=1√2, we can substitute this into the equation:
Bone side=μ0I4π(a2)⋅1√2=μ0I2πa⋅1√2
Since all four sides contribute equally to the magnetic field at the center, we multiply the contribution from one side by 4:
Btotal=4⋅Bone side=4⋅μ0I2πa⋅1√2=2√2μ0Iπa
Thus, the magnetic field at the center of the square loop is given by:
B=2√2μ0Iπa
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionThe dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B1 . When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B2 . The ratio B1B2 is:
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
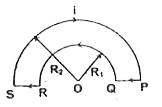 View Solution
View SolutionA current loop in a magnetic field
View SolutionA circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
View SolutionA wire of length l carries a steady current. It is bent first to form a circular plane loop of one turn. The magnetic field at the centre of the loop is B. The same length is now bent more sharply to give a double loop of smaller radius. The magnetic field at the centre caused by the same is
View SolutionA current of2⋅00A exists in a square loop of edge 10⋅0cm. Find the magnetic field B at the centre of the square loop.
View Solution

