A circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30,A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure.
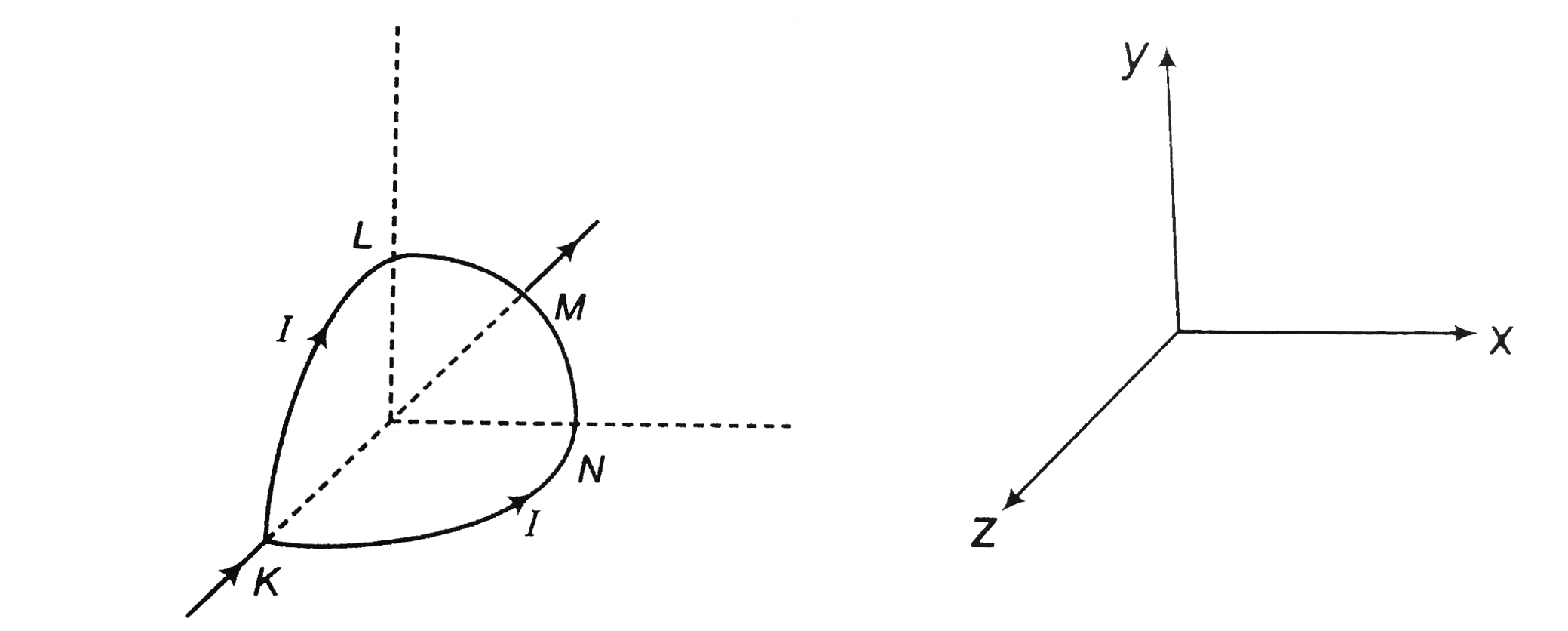
(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
The correct Answer is:A, B, D
a. B at origin BKLM=BKNM
=μ0I4R(−ˆi+ˆj)
Now, we can apply F=q(v×B) for finding force on it.
b. In uniform magnetic field,
FKLM=FKNM=EKM
=I(I×B)
=I[(2R(−ˆk)}×{B0ˆj}]
=(2B0IR)ˆi
:. Net force is two times of the above value.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Video
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Video
Similar Questions
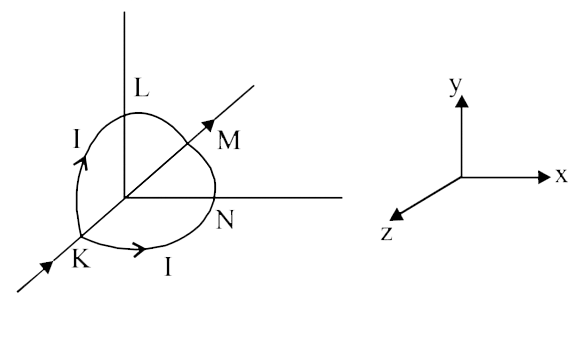
A circular loop of radius R is bent along a diameter and given a shapes as shown in the figure. One of the semicircles (KNM) lies in the x−z plane with their centres and the other one (KLM) in the y−z plane with their centres at the origin. current I is flowing through each of the semi circles as shown in figure.
(a) A particle of charge q is released at the origin with a velocity →v=−v0ˆi. Find the instantaneous force →F on the particle . Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied , determine the force →F1and→F2 on the semicircles KLMandKNM due to the field and the net force →F on the loop.
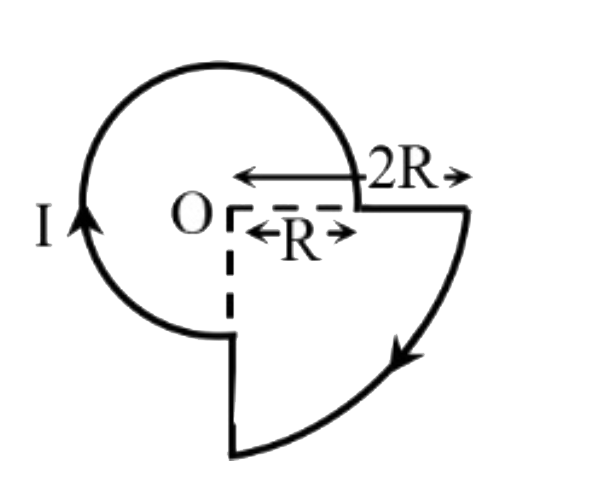
View SolutionA current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is
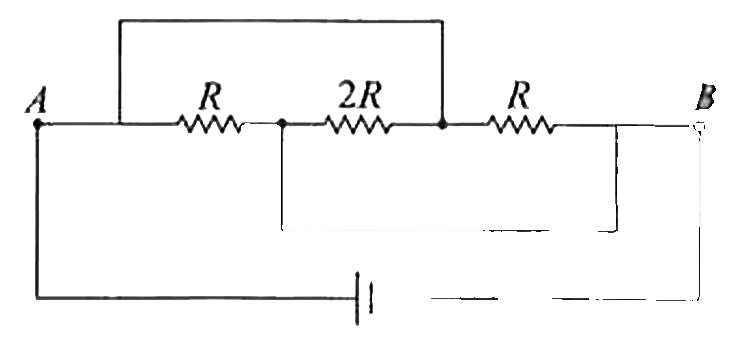
View SolutionIn the figure shown the current flowing through 2R is:
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
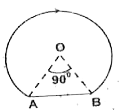
View SolutionA current l flows through a closed loop as shown in figure .The magnetic field at the centre O is
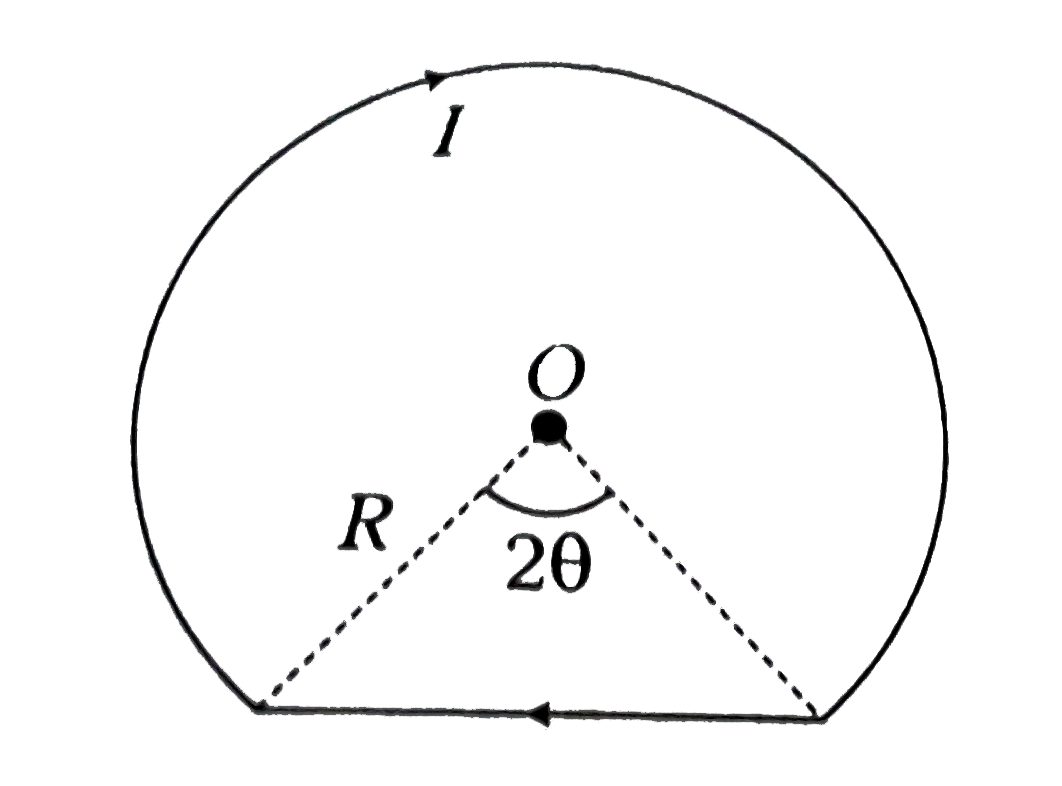
View SolutionA circular loop of wire of radius R is bent about its diameter along two mutually perpendicular planes as shown in Fig. If the loop carries a current I, then determine its magnetic moment.
View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

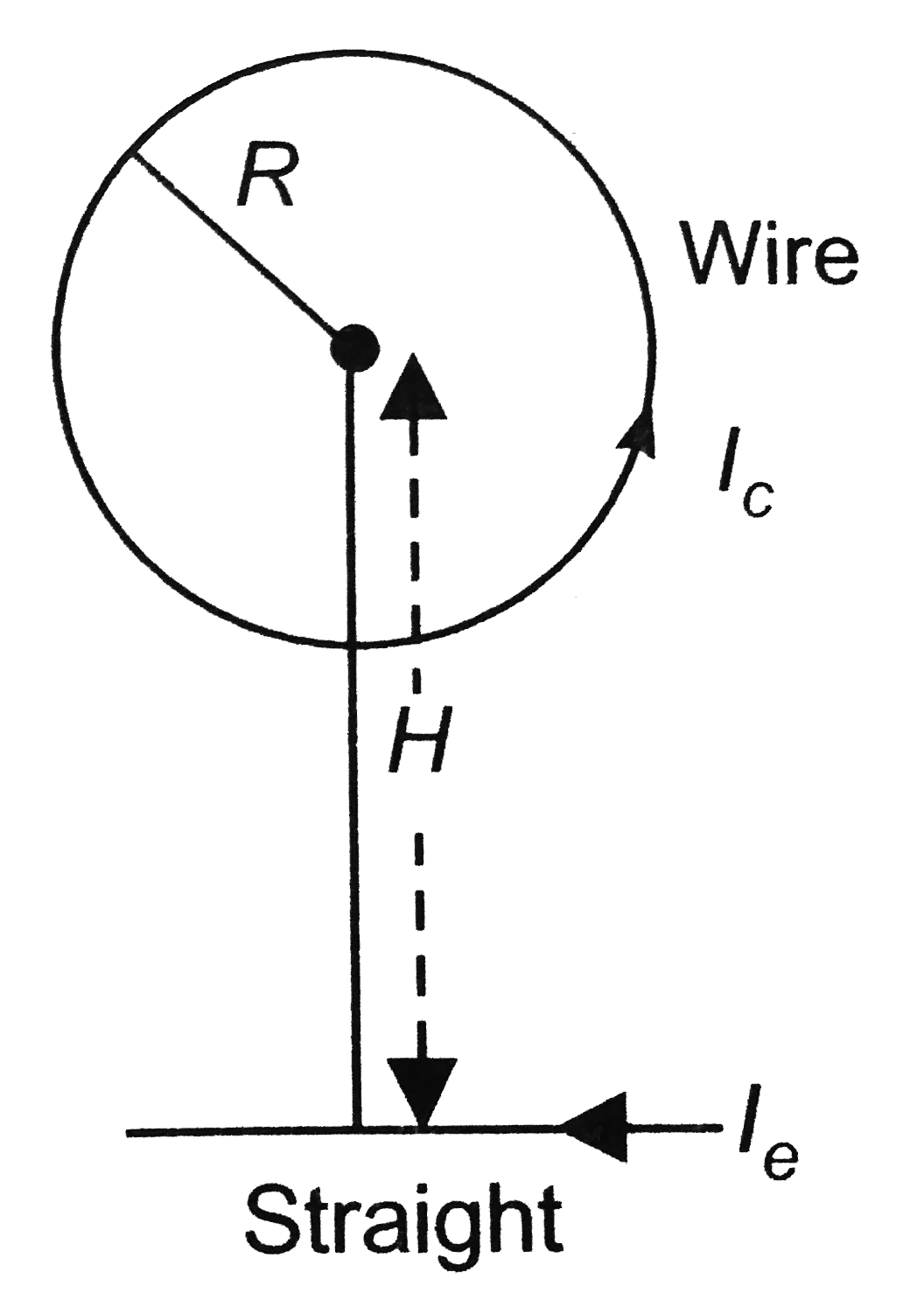
View SolutionCircular loop of a wire and a long straight wire carry current Ic and Ierespectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation H is:
View SolutionThe flux of electric field through the circular region of radius r as shown in the figure is
_PHY_E05_291_Q01.png)
View Solution