A small coil is introduced between the poles of an electromagnet so that its axis coincides with the magnetic field direction. The cross-sectional area of the coil is equal to , the number of turns is . When the coil turns through about its diameter, a galvanometer connected to the coil indicates a charge flowing through it. Find the magnetic induction magnitude between the poles, provided the total resistance of the electric circuit equals .
To solve the problem, we will use the formula for induced charge in a coil rotating in a magnetic field:
Q=−NBAR(cosθ2−cosθ1)
Where:
- Q = induced charge (in coulombs)
- N = number of turns in the coil
- B = magnetic induction (in tesla)
- A = cross-sectional area of the coil (in square meters)
- R = resistance of the circuit (in ohms)
- θ1 and θ2 = initial and final angles of the coil (in degrees)
Step 1: Convert the given values to SI units
- Cross-sectional area S=3.0mm2=3.0×10−6m2
- Charge q=4.5μC=4.5×10−6C
- Resistance R=40Ω
- Number of turns N=60
- Initial angle θ1=0∘
- Final angle θ2=180∘
Step 2: Calculate the change in cosine values
Using the angles:
cosθ1=cos0∘=1
cosθ2=cos180∘=−1
Thus, the change in cosine is:
cosθ2−cosθ1=−1−1=−2
Step 3: Substitute the values into the induced charge formula
Now substituting the values into the formula:
Q=−NBAR(−2)
This simplifies to:
Q=2NBAR
Step 4: Rearranging the formula to solve for B
Rearranging gives us:
B=QR2NA
Step 5: Substitute the known values into the equation
Now substituting the known values:
B=(4.5×10−6C)(40Ω)2×60×(3.0×10−6m2)
Step 6: Calculate the value of B
Calculating the numerator:
4.5×10−6×40=1.8×10−4
Calculating the denominator:
2×60×3.0×10−6=360×10−6=3.6×10−4
Now substituting these into the equation for B:
B=1.8×10−43.6×10−4=0.5T
Final Answer
The magnetic induction magnitude between the poles is:
B=0.5T
- Q = induced charge (in coulombs)
- N = number of turns in the coil
- B = magnetic induction (in tesla)
- A = cross-sectional area of the coil (in square meters)
- R = resistance of the circuit (in ohms)
- θ1 and θ2 = initial and final angles of the coil (in degrees)
- Cross-sectional area S=3.0mm2=3.0×10−6m2
- Charge q=4.5μC=4.5×10−6C
- Resistance R=40Ω
- Number of turns N=60
- Initial angle θ1=0∘
- Final angle θ2=180∘
Using the angles:
cosθ1=cos0∘=1
cosθ2=cos180∘=−1
Thus, the change in cosine is:
cosθ2−cosθ1=−1−1=−2
Now substituting the values into the formula:
Q=−NBAR(−2)
This simplifies to:
Q=2NBAR
Rearranging gives us:
B=QR2NA
Now substituting the known values:
B=(4.5×10−6C)(40Ω)2×60×(3.0×10−6m2)
Calculating the numerator:
4.5×10−6×40=1.8×10−4
Calculating the denominator:
2×60×3.0×10−6=360×10−6=3.6×10−4
Now substituting these into the equation for B:
B=1.8×10−43.6×10−4=0.5T
The magnetic induction magnitude between the poles is:
B=0.5T
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 2 Single Correct
Explore 37 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 2 More Than One Correct
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Objective Questions
Explore 3 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
The self-inductane of a coil having 500 turns is 50 mH. The magnetic flux through the cross-sectional area of the coil while current through it is 8 mA is found to be
View SolutionA small coil of N turns has area A and a current I flows through it. The magnetic dipole moment of this coil will be
View Solution
Knowledge Check
The self inductance of a coil having 400 turns is 10 mH. The magnetic flux through the cross section of the coil corresponding to current 2 mA is
A4×10−5WbB2×10−3WbC3×10−5WbD8×10−3WbWhat is magnetic flux linked with a coil of N turns and cross section area A held with its plane parallel to the field?
ANAB2BNABCNAB4DzeroThe self inductance of an inductance coil having 100 turns is 20 mH. Calculate the magnetic flux through the cross section of the coil corresponding to a current of 4 milliampere. Also, find the total flux
A2×10−5WbB4×10−7WbC8×10−7WbD8×10−5Wb
A circular coil of 200 mm diameter is made of 100 turns of thin wire and carries a current of 50 mA. Find the magnetic field induction at the centre of the coil.
View SolutionA moving coil galvanometer has N numbr of turns in a coil of effective area A, it carries a current I. The magnetic field B is radial. The torque acting on the coil is
View SolutionA flat circular coil of n turns, area A and resitance R is placed in a uniform magnetic field B. The pane of coil is initially perpedicular of B. when the coil is rotated through an angle of 180∘ about one of its diameter, a charge Q1 flows through the coil When the same coil after charge Q2 flows through it. then Q2/Q1 is
View SolutionMagnetic flux of 5 microweber is linked with a coil, when a current of 1mA flows through it. What is the self-inductance of the coil?
View SolutionA small coil C with N=200 turns is mounted on one end of a balance beam and introduced between the poles of an electromagnetic as shown in Fig. The area of the coils is S=1cm2, the length of the right arm of the balance beam is l=30cm. When there is no current in the coil the balance is in equilibrium. On passing is a currentI=22mA through the coil, equilibrium is restored by putting an additional weight of mass m=60mg on the balance pan. Find the magnetic induction field (in terms of x10−1T) between the poles of the electromagnetic assuming it to be uniform.
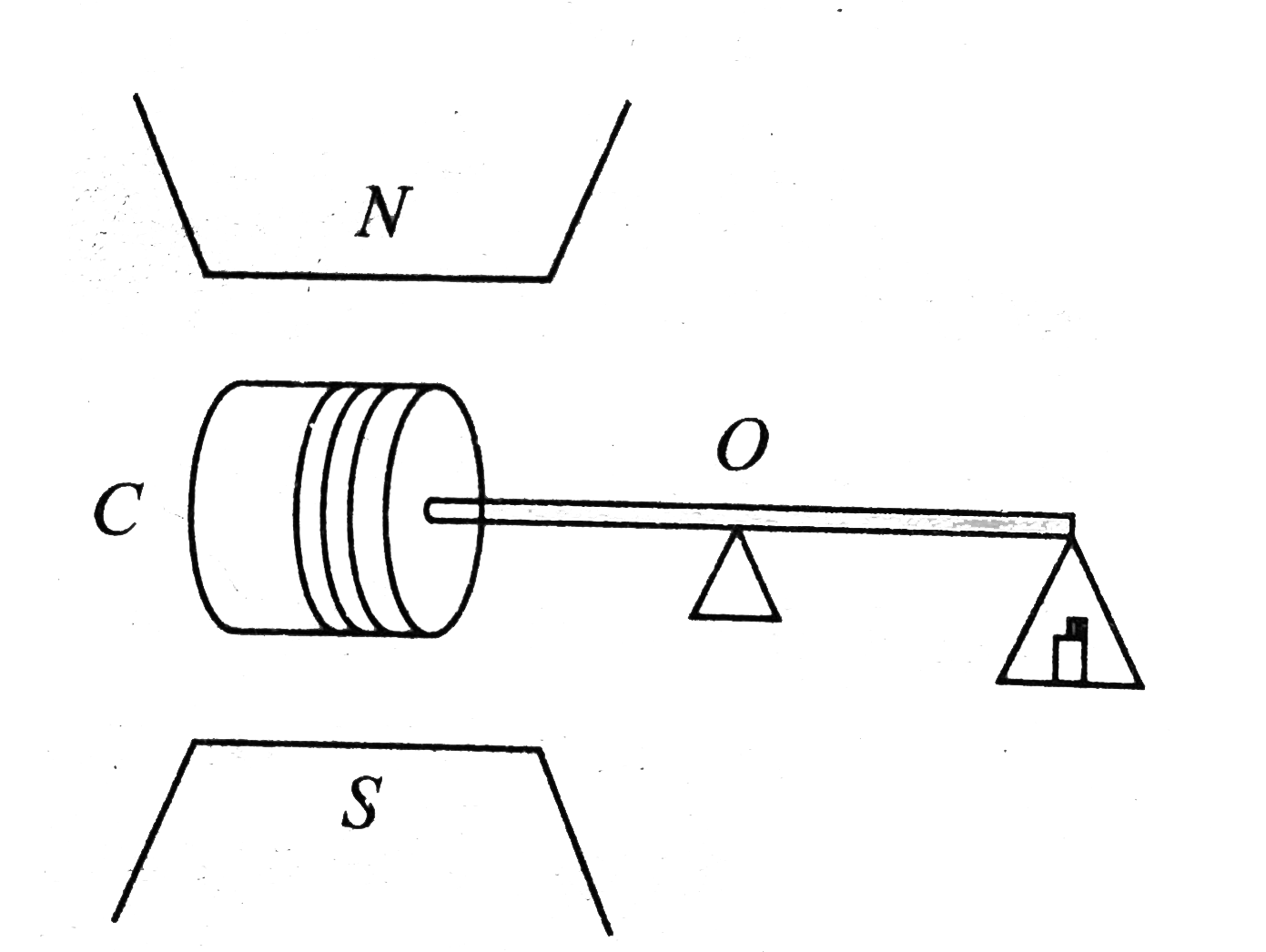
View Solution