A complex current wave is given by . Its average value over one time period is given as
0
The correct Answer is:B
To find the average value of the given complex current wave i=(5+5sin(100ωt))A over one time period, we can follow these steps:
Step 1: Identify the components of the current wave
The current wave consists of a constant component and a sinusoidal component:
- Constant component: 5A
- Sinusoidal component: 5sin(100ωt)A
Step 2: Write the formula for average value
The average value of a function i(t) over one time period T is given by:
Iavg=1T∫T0i(t)dt
Step 3: Determine the time period T
The time period T for the sinusoidal component sin(100ωt) is:
T=2π100ω
Step 4: Set up the integral
Now we can set up the integral for the average value:
Iavg=1T∫T0(5+5sin(100ωt))dt
Step 5: Split the integral
We can split the integral into two parts:
Iavg=1T(∫T05dt+∫T05sin(100ωt)dt)
Step 6: Evaluate the first integral
The first integral is straightforward:
∫T05dt=5T
Step 7: Evaluate the second integral
The second integral, ∫T05sin(100ωt)dt, evaluates to zero over one complete cycle because the positive and negative areas cancel each other out:
∫T05sin(100ωt)dt=0
Step 8: Combine results
Now, substituting back into the average value formula:
Iavg=1T(5T+0)=5
Final Answer
Thus, the average value of the current wave over one time period is:
Iavg=5A
The current wave consists of a constant component and a sinusoidal component:
- Constant component: 5A
- Sinusoidal component: 5sin(100ωt)A
The average value of a function i(t) over one time period T is given by:
Iavg=1T∫T0i(t)dt
The time period T for the sinusoidal component sin(100ωt) is:
T=2π100ω
Now we can set up the integral for the average value:
Iavg=1T∫T0(5+5sin(100ωt))dt
We can split the integral into two parts:
Iavg=1T(∫T05dt+∫T05sin(100ωt)dt)
The first integral is straightforward:
∫T05dt=5T
The second integral, ∫T05sin(100ωt)dt, evaluates to zero over one complete cycle because the positive and negative areas cancel each other out:
∫T05sin(100ωt)dt=0
Now, substituting back into the average value formula:
Iavg=1T(5T+0)=5
Thus, the average value of the current wave over one time period is:
Iavg=5A
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2More Than One Correct
8 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Comprehension
6 Videos
- ALTERNATING CURRENTBOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective
6 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
Similar Questions
Knowledge Check
The equation of a simple harmonic wave is given by Y=5sinπ2(100t−x), where x and y are in metre and time is in second. The time period of the wave (m seconds) will be
A0.04B0.01C1D5
Average value of KE and PE over entire time period is
View SolutionThe average value of voltage (V) in one time period will be
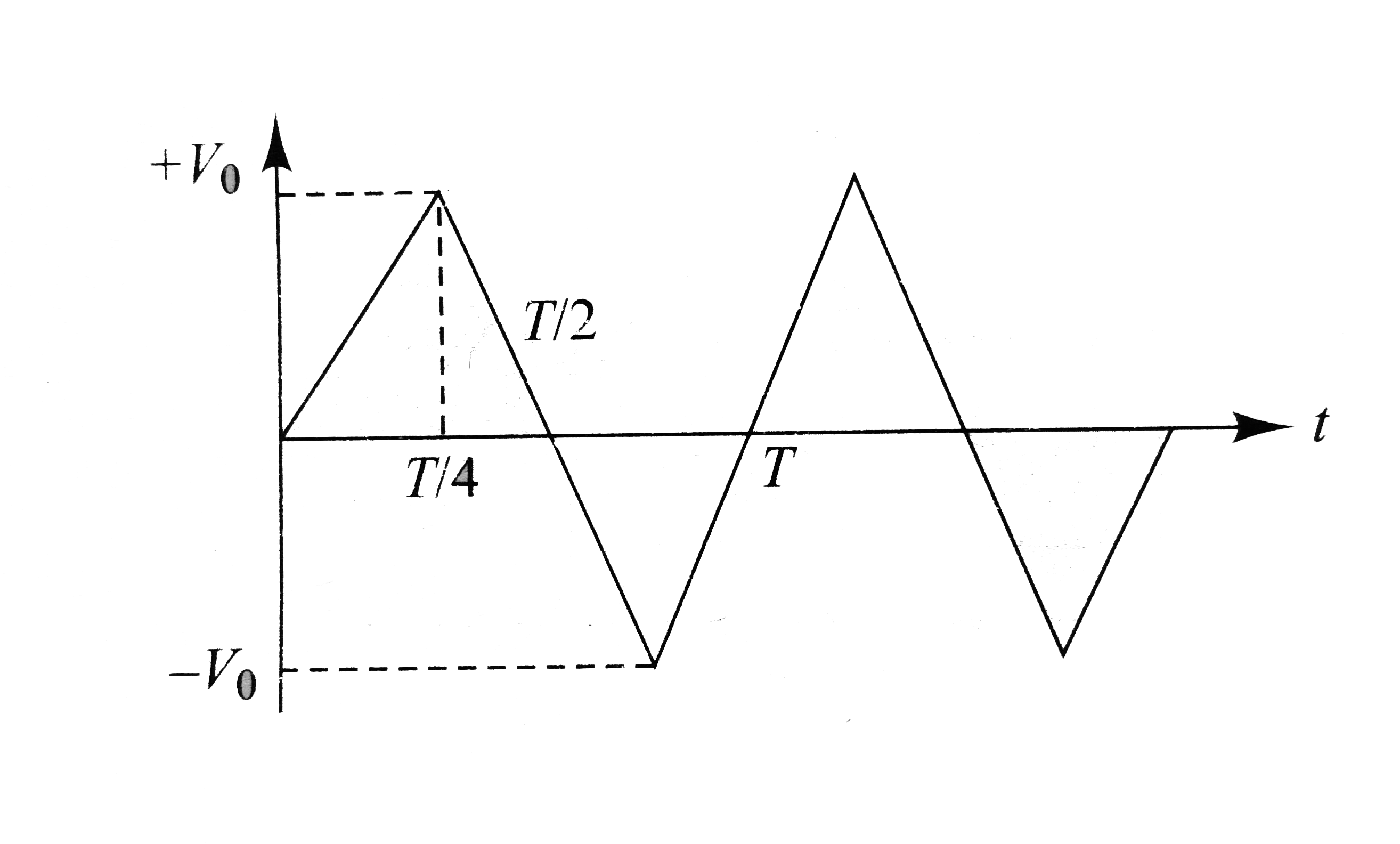
View SolutionThe current is given by i=i0+i0 sin omega t then its r.m.s value will be
View SolutionAn AC current is given by i= 3+4 sinwt ,then its effective value
View SolutionThe electric field of a plane electromagnetic wave is given by
→E=E0(ˆx+ˆy)sin(kz−ωt)
Its magnetic field will be given by :
View SolutionAn alternative current is given by I=(100√2sint)A. The RMS value of current is
View SolutionAn alternating current is given by
I=i1cosωt+i2sinωt.
The rms current is given by
View Solution
