In a series L−C−R circuit, currenrt in the circuit is 11A when the applied voltage is 220V. voltage across the caspcitor is 200V. If the value of resistor is 20Ω, then the voltage across the unknown inductor is
zero
200V
20V
none of these
The correct Answer is:B
To solve the problem, we need to find the voltage across the unknown inductor in a series L-C-R circuit. We are given the following information:
- Current in the circuit (I) = 11 A
- Applied voltage (V) = 220 V
- Voltage across the capacitor (V_C) = 200 V
- Resistance (R) = 20 Ω
1. Calculate the Impedance (Z) of the Circuit:
The impedance (Z) in a series L-C-R circuit can be calculated using the formula:
Z=VI
Substituting the values:
Z=220V11A=20Ω
2. Determine the Condition of Resonance:
Since the impedance (Z) is equal to the resistance (R), we can conclude that the circuit is at resonance. This implies that the inductive reactance (X_L) is equal to the capacitive reactance (X_C):
XL=XC
3. Calculate the Capacitive Reactance (X_C):
The capacitive reactance can be calculated using the formula:
XC=VCI
Substituting the values:
XC=200V11A≈18.18Ω
4. Find the Inductive Reactance (X_L):
Since we established that XL=XC at resonance:
XL=18.18Ω
5. Calculate the Voltage across the Inductor (V_L):
The voltage across the inductor can be calculated using the formula:
VL=XL⋅I
Substituting the values:
VL=18.18Ω⋅11A≈200V
Conclusion:
The voltage across the unknown inductor is approximately 200 V.
- Applied voltage (V) = 220 V
- Voltage across the capacitor (V_C) = 200 V
- Resistance (R) = 20 Ω
The impedance (Z) in a series L-C-R circuit can be calculated using the formula:
Z=VI
Substituting the values:
Z=220V11A=20Ω
Since the impedance (Z) is equal to the resistance (R), we can conclude that the circuit is at resonance. This implies that the inductive reactance (X_L) is equal to the capacitive reactance (X_C):
XL=XC
The capacitive reactance can be calculated using the formula:
XC=VCI
Substituting the values:
XC=200V11A≈18.18Ω
Since we established that XL=XC at resonance:
XL=18.18Ω
The voltage across the inductor can be calculated using the formula:
VL=XL⋅I
Substituting the values:
VL=18.18Ω⋅11A≈200V
The voltage across the unknown inductor is approximately 200 V.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level- 2More Than One Correct8videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level 2 Comprehension6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Level - 1 Subjective6videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
Similar Questions
In the series L−C−R circuit shown in the figure, the rms voltage across the resistor and inductor are 400 V and 700 V respectively. If the applied voltage is E=500√2sin(ωt), then the peak voltage across the capacitor is
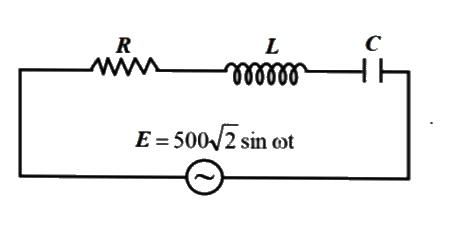 View Solution
View SolutionIn a series L−C circuit, the applied voltage is V0. if omega is very low, then the voltage drop across the inductor VL and capacitor VC are
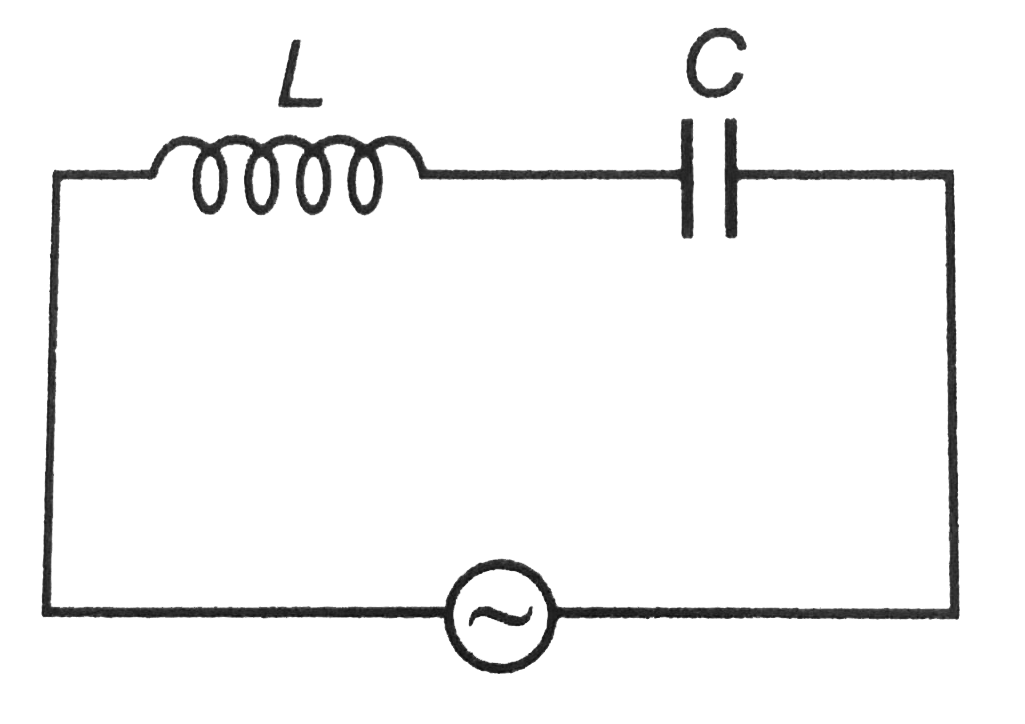 .View Solution
.View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
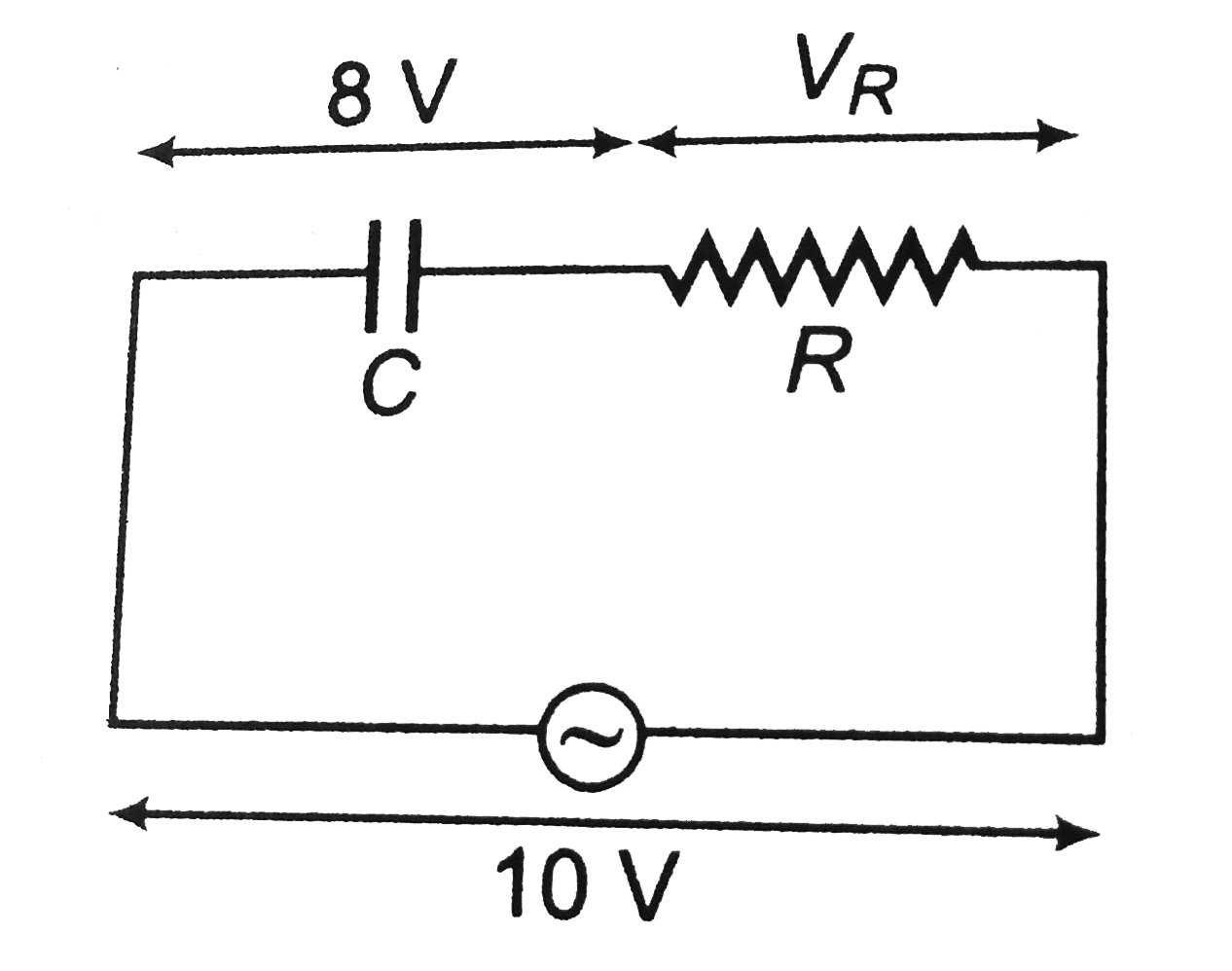 .View Solution
.View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
 .View Solution
.View SolutionAn ac source of 50 V (r.m.s value) is connected across a series R - C circuit. If the r.m.s voltage across the resistor is 40 V, then the r.m.s voltage across the capacitor is
View SolutionIn series LCR circuit, the phase difference between voltage across L and voltage across C is
View SolutionIn the given circuit the R.M.S values of voltages across the capacitor C, inductor L and resistor R1 are 12V, 10V and 5 V respectively. Then the peak voltage across R2 is
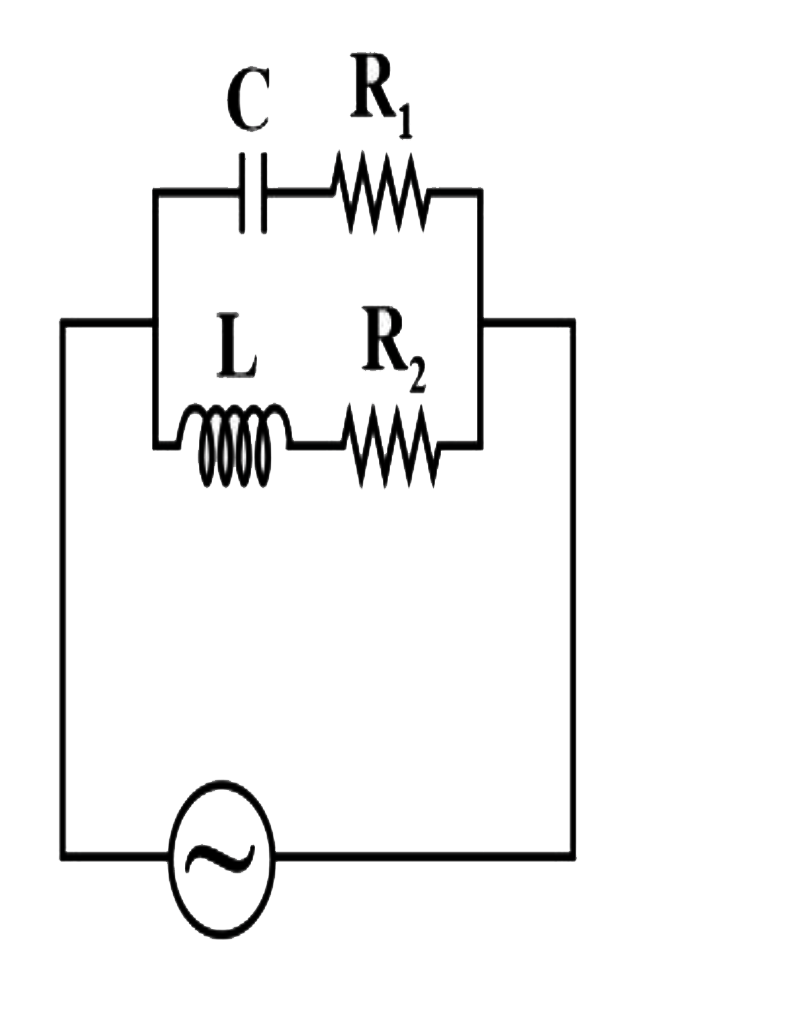 View Solution
View SolutionIn the circuit the rms value of voltage across the capacitor C, inductor L and resister R1 are respectively 5√5V, 10 V and 5V. Then the peak voltage a cross R2 is
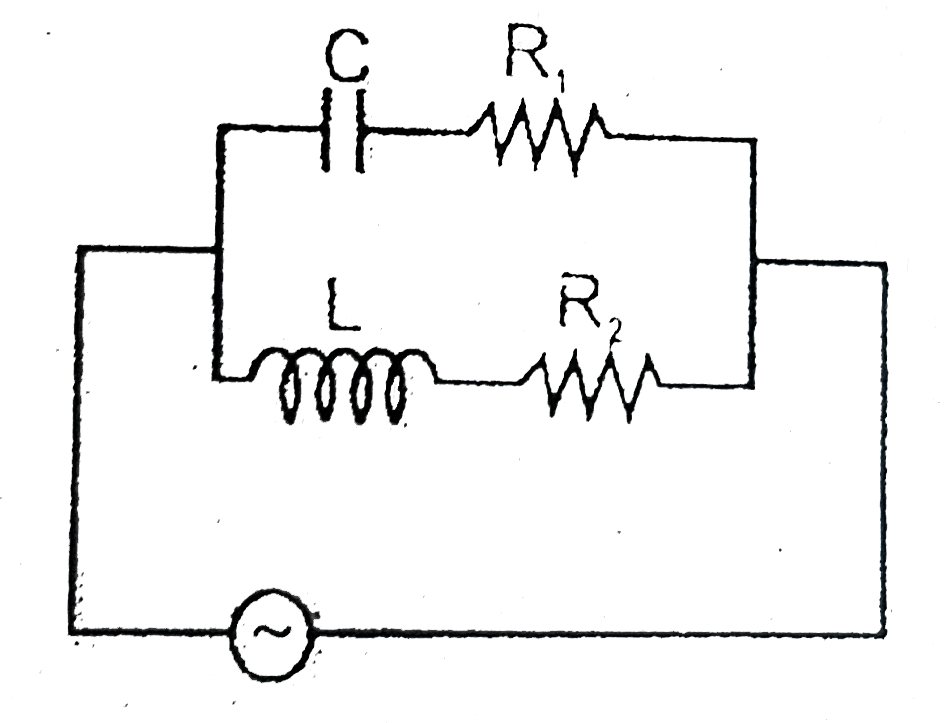 View Solution
View SolutionFor the circuit shown in figure, determine the voltage across 4Ω resistors in volt ?
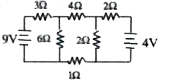 View Solution
View SolutionIn an LCR series ac circuit , the voltage across each of the components , L,C and R is 50 V . The voltage across the LC combination will be :
View Solution

