A hollow sphere of glass of inner and outer radii R and 2R respectively has a small mark on its inner surface. This mark is observed from a point outside the sphere such that the centre of the sphere lies in between. Prove that the mark will appear nearer than it really it, by a distance (μ−1)(R)/(3μ−1)
The correct Answer is:A
To solve the problem step by step, we need to analyze the refraction of light through the hollow glass sphere and derive the expression for the apparent distance of the mark from the observer.
1. Understanding the Geometry:
- We have a hollow glass sphere with an inner radius R and an outer radius 2R.
- A mark M is located on the inner surface of the sphere.
- The observer is positioned outside the sphere, with the center of the sphere in between.
2. Identify the Refraction Surfaces:
- The light from the mark M will undergo refraction at two spherical surfaces:
- Surface 1 (inner surface of the sphere).
- Surface 2 (outer surface of the sphere).
3. Apply the Refraction Formula:
- For refraction at a spherical surface, we use the formula:
n2v−n1u=n2−n1R
- Here, n1 is the refractive index of air (1), n2 is the refractive index of glass (μ), u is the object distance, and v is the image distance.
4. Refraction at Surface 1:
- The object distance u for surface 1 (from the center to the mark) is −2R (negative because it is in the opposite direction of the incident ray).
- The radius R for surface 1 is −R (also negative).
- Substituting into the formula:
μv1−1−2R=μ−1−R
- Rearranging gives:
μv1=μ−1−R+12R
- Solving for v1:
v1=−2μR2μ−1
5. Refraction at Surface 2:
- The image formed by surface 1 acts as the object for surface 2.
- The object distance u for surface 2 is R+|v1|.
- Therefore, substituting v1:
u=R+2μR2μ−1
- The radius R for surface 2 is −2R.
- Using the refraction formula again:
1v2−μu=1−μ−2R
- Rearranging gives:
1v2=1−μ−2R+μu
6. Calculate v2:
- Substitute u into the equation and solve for v2:
v2=−2(4μ−1)R3μ−1
7. Finding the Apparent Distance:
- The apparent distance d that the mark appears closer is given by:
d=|BM|−|BI2|=3R−|v2|
- Substituting |v2|:
d=3R−(−2(4μ−1)R3μ−1)
- Simplifying gives:
d=(μ−1)R3μ−1
Final Result:
Thus, we have shown that the mark will appear nearer than it really is by a distance of:
(μ−1)R3μ−1
- We have a hollow glass sphere with an inner radius R and an outer radius 2R.
- A mark M is located on the inner surface of the sphere.
- The observer is positioned outside the sphere, with the center of the sphere in between.
- The light from the mark M will undergo refraction at two spherical surfaces:
- Surface 1 (inner surface of the sphere).
- Surface 2 (outer surface of the sphere).
- For refraction at a spherical surface, we use the formula:
n2v−n1u=n2−n1R
- Here, n1 is the refractive index of air (1), n2 is the refractive index of glass (μ), u is the object distance, and v is the image distance.
- The object distance u for surface 1 (from the center to the mark) is −2R (negative because it is in the opposite direction of the incident ray).
- The radius R for surface 1 is −R (also negative).
- Substituting into the formula:
μv1−1−2R=μ−1−R
- Rearranging gives:
μv1=μ−1−R+12R
- Solving for v1:
v1=−2μR2μ−1
- The image formed by surface 1 acts as the object for surface 2.
- The object distance u for surface 2 is R+|v1|.
- Therefore, substituting v1:
u=R+2μR2μ−1
- The radius R for surface 2 is −2R.
- Using the refraction formula again:
1v2−μu=1−μ−2R
- Rearranging gives:
1v2=1−μ−2R+μu
- Substitute u into the equation and solve for v2:
v2=−2(4μ−1)R3μ−1
- The apparent distance d that the mark appears closer is given by:
d=|BM|−|BI2|=3R−|v2|
- Substituting |v2|:
d=3R−(−2(4μ−1)R3μ−1)
- Simplifying gives:
d=(μ−1)R3μ−1
Thus, we have shown that the mark will appear nearer than it really is by a distance of:
(μ−1)R3μ−1
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Comprehension Based3videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
Does the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?View SolutionA hollow sphere of glass of R.I .n has small mark M on its interior surface which is observed by an observer O from a point outside the sphere, .C is centre of the sphere. The inner cavity (air) is concentric with the external surface and thickness of the glass is every where equal to the radius of the inner surface. Find the distance by which the mark will appear nearer than it really is in terms of n and R assuming paraxial rays.
_E01_156_Q01.png) View Solution
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the
 View Solution
View SolutionA hollow metallic sphere has inner and outer radii, respectively as 5 cm and 10 cm if the mass of the sphere is 2.5 kg, find (a) density of the material, (b) relative density of the material of the sphere.
View SolutionA small filament is at the centre of a hollow glass sphere of inner and outer radii 8 cm and 9 cm respectively. The refractive index of glass is 1.50. Calculate the position of the image of the filament when viewed from outside the sphere.
View SolutionIn a conducting hollow sphere of inner and outer radii 5 cm and 10 cm, respectively, a point charge 1 C is placed at point A, that is 3 cm from the center C of the hollow sphere. An external uniform electric field to magnitude 20NC−1 is also applied. Net electric force on this charge is 15 N, away from the center of the sphere as shown. Find the magnitude of net force exerted on the charge placed at point A by the induced charges on the sphere
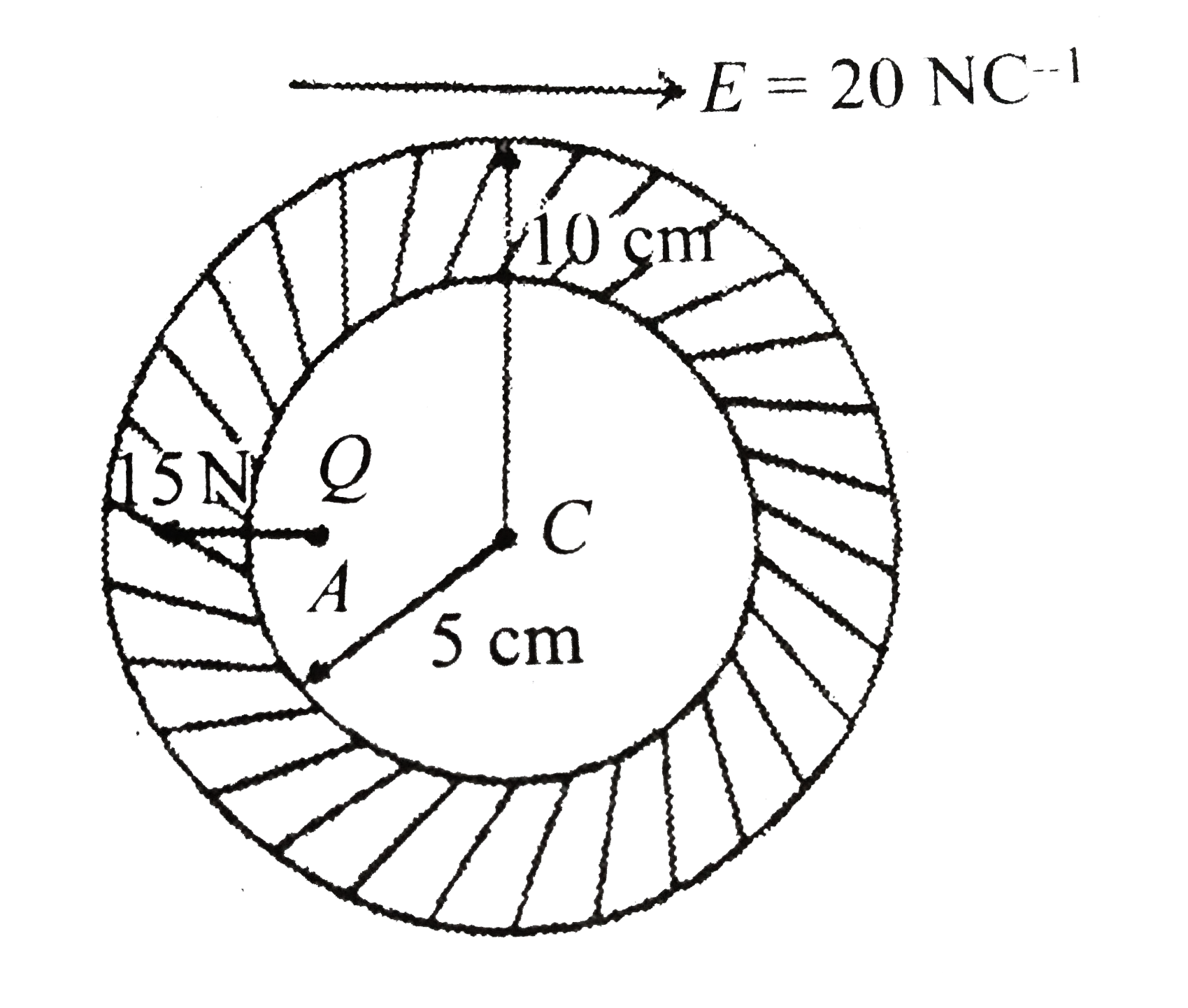 View Solution
View SolutionA hollow conducting sphere of radius R has a charge (+Q) on its surface. What is the electric potential within the
sphere at a distance r=R3 from its centre ?View SolutionThere is a small black dot at the centre C of a solid glass sphere of refractive index μ. When seen from outside, the dot will appear to be located
View SolutionA hollow spherical conductor of radius r potential of 100 V at its outer surface. The potential inside the hollow at a distance ofr2 from its centre is
View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is
 View Solution
View Solution

