A small object is placed on the principal axis of concave spherical mirror of radius 20cm at a distance of 30cm. By how much will the position of the image alter only after mirror, when a parallel-sided slab of glass of thickness 6cm and refractive index 1.5 is introduced between the centre of curvature and the object? The parallel sides are perpendicular to the principal axis.
The correct Answer is:A, C, D
To solve the problem step by step, we will follow these steps:
Step 1: Determine the Focal Length of the Concave Mirror
The focal length (F) of a concave mirror is given by the formula:
F=R2
where R is the radius of curvature.
Given:
- Radius of curvature, R=20cm
Calculating the focal length:
F=20cm2=10cm
Step 2: Use the Mirror Formula to Find the Initial Image Position (V1)
The mirror formula is:
1F=1V+1U
where:
- U is the object distance (negative for concave mirrors),
- V is the image distance.
Given:
- Object distance, U=−30cm
Substituting the values into the mirror formula:
110=1V1+1−30
Rearranging gives:
1V1=110+130
Finding a common denominator (30):
1V1=330+130=430
V1=304=7.5cm
Step 3: Calculate the Shift Due to the Glass Slab
The formula for the shift (d) caused by a glass slab is:
d=t(1−1μ)
where:
- t is the thickness of the slab,
- μ is the refractive index.
Given:
- Thickness of the slab, t=6cm
- Refractive index, μ=1.5
Calculating the shift:
d=6(1−11.5)=6(1−23)=6(13)=2cm
Step 4: Adjust the Object Distance (U) After Introducing the Slab
The new object distance U′ after introducing the slab is:
U′=U+d
Substituting the values:
U′=−30cm+2cm=−28cm
Step 5: Use the Mirror Formula to Find the New Image Position (V2)
Using the new object distance in the mirror formula:
1F=1V2+1U′
Substituting the values:
110=1V2+1−28
Rearranging gives:
1V2=110+1−28
Finding a common denominator (140):
1V2=14140−5140=9140
V2=1409≈15.56cm
Step 6: Calculate the Change in Image Position
The change in image position is:
ΔV=V2−V1
Substituting the values:
ΔV=15.56cm−7.5cm=8.06cm
Final Answer
The position of the image alters by approximately 8.06cm after the introduction of the glass slab.
---
The focal length (F) of a concave mirror is given by the formula:
F=R2
where R is the radius of curvature.
- Radius of curvature, R=20cm
F=20cm2=10cm
The mirror formula is:
1F=1V+1U
where:
- U is the object distance (negative for concave mirrors),
- V is the image distance.
- Object distance, U=−30cm
110=1V1+1−30
1V1=110+130
1V1=330+130=430
V1=304=7.5cm
The formula for the shift (d) caused by a glass slab is:
d=t(1−1μ)
where:
- t is the thickness of the slab,
- μ is the refractive index.
- Thickness of the slab, t=6cm
- Refractive index, μ=1.5
d=6(1−11.5)=6(1−23)=6(13)=2cm
The new object distance U′ after introducing the slab is:
U′=U+d
Substituting the values:
U′=−30cm+2cm=−28cm
Using the new object distance in the mirror formula:
1F=1V2+1U′
Substituting the values:
110=1V2+1−28
1V2=110+1−28
1V2=14140−5140=9140
V2=1409≈15.56cm
The change in image position is:
ΔV=V2−V1
Substituting the values:
ΔV=15.56cm−7.5cm=8.06cm
The position of the image alters by approximately 8.06cm after the introduction of the glass slab.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Comprehension Based3videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
An object is kept on the principal axis of a concave mirror of focal length 10cm, at a distance of 15 cm from its pole. The image formed by the mirror is:
AVirtual and magnifiedBVirtual and diminishedCReal and magnifiedDReal and diminished
An extended object is placed perpendicular to the principal axis of a concave mirror of radius of curvature 20cm at a distance of 15 cm from the pole. Find the lateral magnification produced.
View SolutionAn extended object is placed perpendicular to the principal axis of a concave mirror of radius of curvature 20cm at a distance of 15 cm from the pole. Find the lateral magnification produced.
View SolutionA point object is placed on principal axis of a concave mirror of radius of curvature 20cm at a distance 31cm from poll of the mirror. A glass slab of thikness 3cm and refractive index 1.5 is placed between object and mirror as shown in the figure. Find the distance (in cm) of final image formed by the system from the mirror.
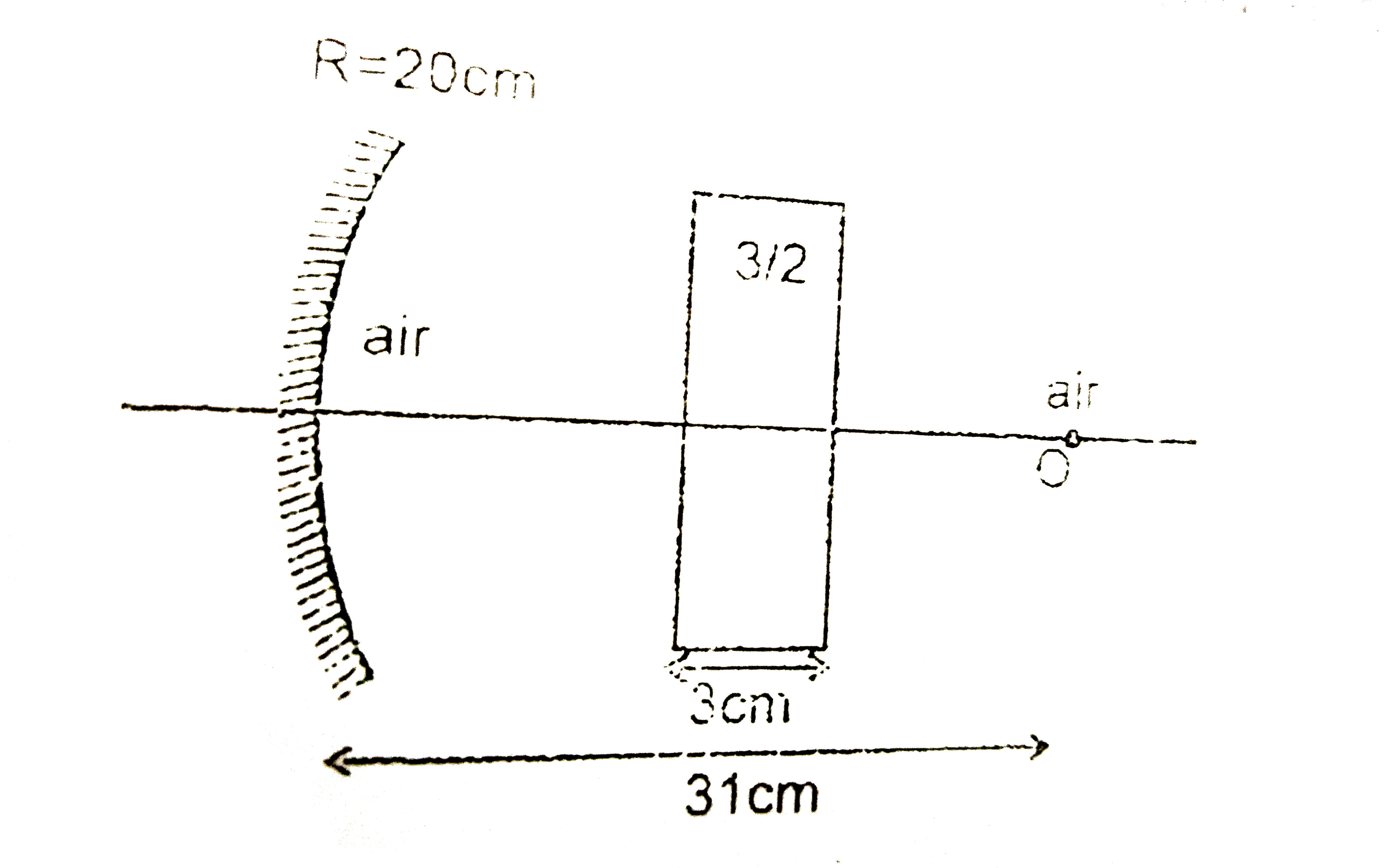 View Solution
View SolutionA 1 cm object is placed perpendicular to the principal axis of a convex mirror of focal length 7.5 cm. Find its distance from the mirror if the image formed is 0.6 cm in size.
View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
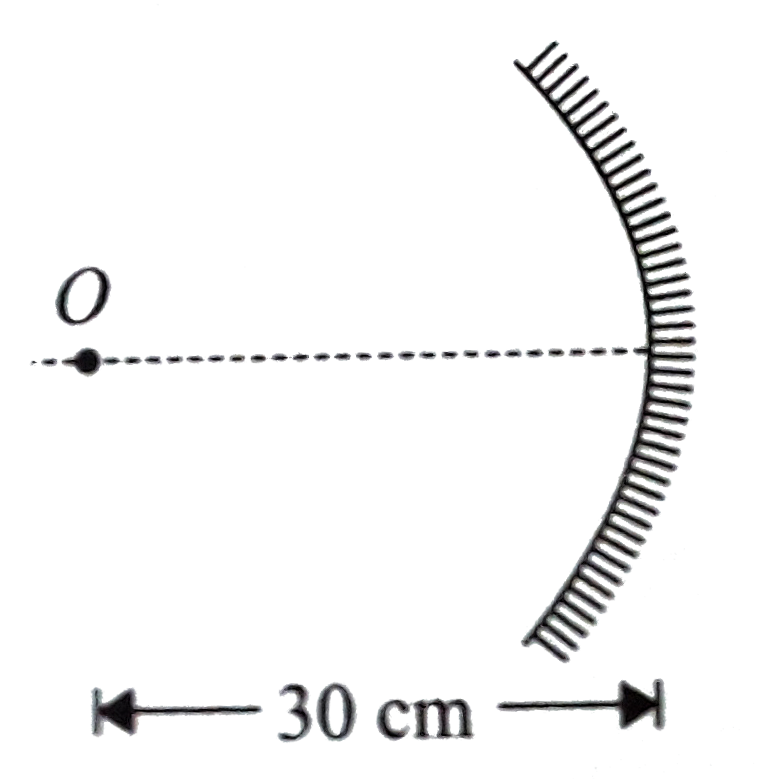
Q. Image formed by mirror isView Solution

