A radioactive isotope is being produced at a constant rate dN/dt=R in an experiment. The isotope has a half-life t1/2.Show that after a time t>>t1/2,the number of active nuclei will become constant. Find the value of this constant.
(a) AT
(b) AT1n2
(c) AT 1n2
(d) AT1n2
The correct Answer is:D
To solve the problem, we need to analyze the behavior of a radioactive isotope being produced at a constant rate R and its decay over time. The goal is to show that after a time much greater than the half-life t1/2, the number of active nuclei becomes constant, and to find the value of this constant.
1. Define the Variables:
- Let N(t) be the number of active nuclei at time t.
- The rate of production of the isotope is given as dNdt=R.
- The decay of the isotope is characterized by its decay constant λ, which is related to the half-life t1/2 by the formula:
λ=ln(2)t1/2
2. Set Up the Differential Equation:
- The change in the number of active nuclei over time can be expressed as:
dNdt=R−λN
- Here, R is the rate of production, and λN is the rate of decay of the nuclei.
3. Rearranging the Equation:
- Rearranging the equation gives:
dNdt+λN=R
4. Solve the Differential Equation:
- This is a first-order linear ordinary differential equation. To solve it, we can use an integrating factor:
μ(t)=eλt
- Multiply the entire equation by the integrating factor:
eλtdNdt+λeλtN=Reλt
- The left-hand side can be rewritten as:
ddt(eλtN)=Reλt
5. Integrate Both Sides:
- Integrating both sides with respect to t:
eλtN=∫Reλtdt+C
- The integral on the right side is:
∫Reλtdt=Rλeλt+C
- Thus, we have:
eλtN=Rλeλt+C
6. Solve for N(t):
- Dividing through by eλt:
N(t)=Rλ+Ce−λt
7. Determine the Constant C:
- As t→∞, the term Ce−λt approaches zero. Therefore, the number of active nuclei approaches:
N(t)→Rλ
- This shows that after a long time (i.e., t≫t1/2), the number of active nuclei becomes constant.
8. Final Expression for the Constant:
- Substituting λ=ln(2)t1/2:
Nconstant=Rλ=Rt1/2ln(2)
Conclusion:
After a time much greater than the half-life t1/2, the number of active nuclei becomes constant and is given by:
Nconstant=Rt1/2ln(2)
- Let N(t) be the number of active nuclei at time t.
- The rate of production of the isotope is given as dNdt=R.
- The decay of the isotope is characterized by its decay constant λ, which is related to the half-life t1/2 by the formula:
λ=ln(2)t1/2
- The change in the number of active nuclei over time can be expressed as:
dNdt=R−λN
- Here, R is the rate of production, and λN is the rate of decay of the nuclei.
- Rearranging the equation gives:
dNdt+λN=R
- This is a first-order linear ordinary differential equation. To solve it, we can use an integrating factor:
μ(t)=eλt
- Multiply the entire equation by the integrating factor:
eλtdNdt+λeλtN=Reλt
- The left-hand side can be rewritten as:
ddt(eλtN)=Reλt
- Integrating both sides with respect to t:
eλtN=∫Reλtdt+C
- The integral on the right side is:
∫Reλtdt=Rλeλt+C
- Thus, we have:
eλtN=Rλeλt+C
- Dividing through by eλt:
N(t)=Rλ+Ce−λt
- As t→∞, the term Ce−λt approaches zero. Therefore, the number of active nuclei approaches:
N(t)→Rλ
- This shows that after a long time (i.e., t≫t1/2), the number of active nuclei becomes constant.
- Substituting λ=ln(2)t1/2:
Nconstant=Rλ=Rt1/2ln(2)
After a time much greater than the half-life t1/2, the number of active nuclei becomes constant and is given by:
Nconstant=Rt1/2ln(2)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 More Than One Correct6videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Comprehension Based3videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 1 Subjective Questions1videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective23videos
MODERN PHYSICS - 1
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
Similar Questions
A radiaocatice isotope is being produced at a constant rate X. Half-life of the radioactive substance is Y. After some time, the number of radioactive nuceli become constant. The value of this constant is .
View SolutionA rodiactive nucleus is being produced at a constant rate α per second Its decay constant is λ If N0 are the number of nuclie at tieme t=O then, maximum number of nuclei possible are
View Solution
Knowledge Check
- Question 1 - Select One
Nuclei of a radioactive element A are being produced at a constant rate α. The element has a decay constant λ. At time t=0, there are N0 nuclei of the element.
(a) Calculate the number N of nuclei of A at time t.
(b) If α=2N0λ, calculate the number of nuclei of A after one half-life of A, and also the limiting value of N as t→∞.A1λ[α+(α−N0λ)e−λt]B1λ[α−(α−N0λ)e−λt]Cλ[α−(α−N0λ)e−λt]D[α−(N0λ−α)e−λt]
A radioacitve nucleus is being produced at a constant rate α per second. Its decay constant is λ. If N0 are the number of nuclei at time t=0, then maximum number of nuceli possible are .
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/2. At the time t=0, there are N0nuclei of the element X.
The number NX of nuclei of X at time t=T1/2 is .View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/3. At the time t=0, there are N0nuclei of the element X.
The number NY of nuclei of Y at time t is .View Solution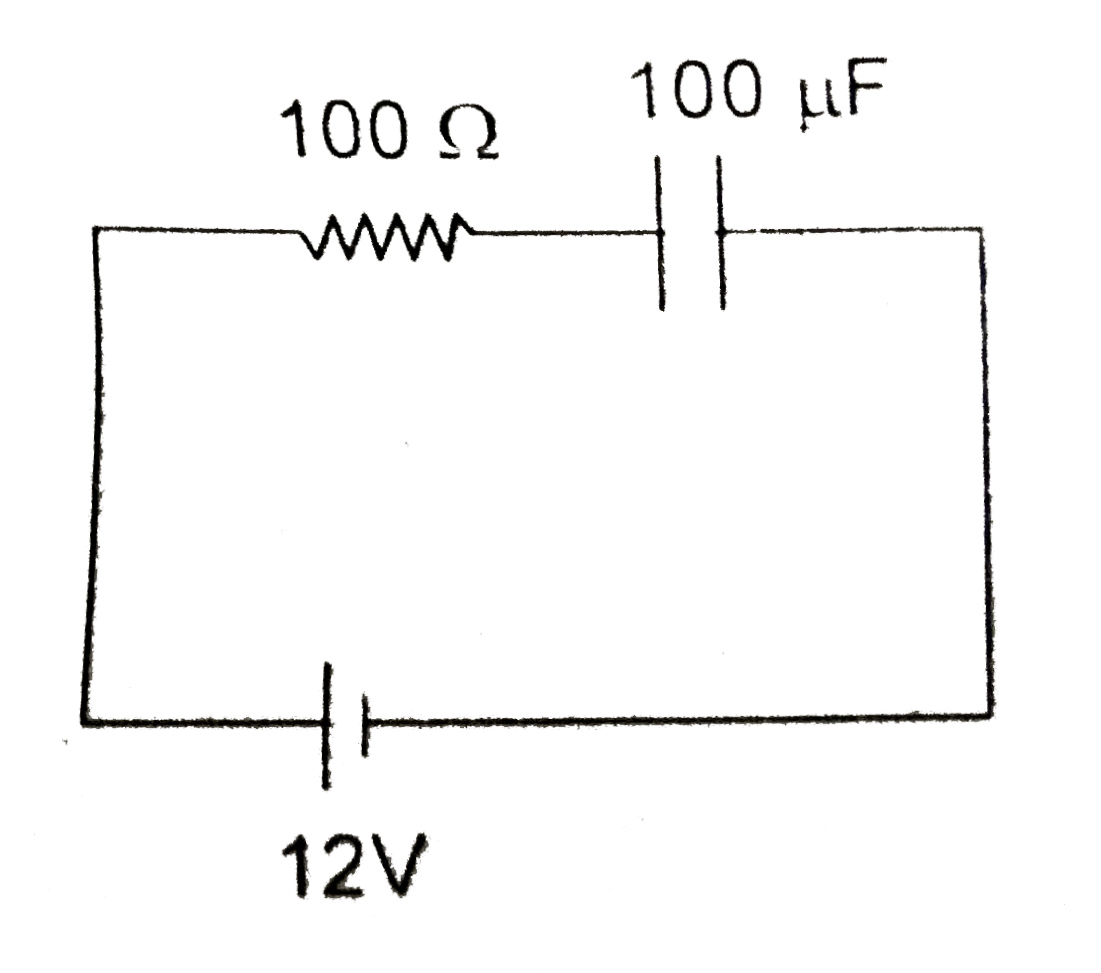
The value of displacement current at t=1 time constant isView SolutionThalassemia and sickle cell anemia are caued due to problem in globin molecule synthesis . Select the correct statement.
View SolutionNuclei of a radioactive element A are being produced at a constant rate α. The element has a decay constant λ. At time t=0, there are N0 nuclei of the element.
(a) Calculate the number N of nuclei of A at time t.
(b) If α=2N0λ, calculate the number of nuclei of A after one half-life of A, and also the limiting value of N as t→∞.View SolutionA radioactive substance (A) is produced at a constant rate which decays with a decay constant λ to form stable substance (B).If production of A starts at t=0 . Find (i)The number of nuclei of A and (ii)Number of nuclei of B at any time t.
View Solution

