A block of mass m is hung vertically from an elastic thread of force constant mg/a. Initially the thread was at its natural length and the block is allowed to fall freely. Kinetic energy of the block when it passes through the equilibrium position will be
mga
mga2
zero
2mga
The correct Answer is:B
To solve the problem, we need to determine the kinetic energy of a block of mass m when it passes through the equilibrium position after being released from rest. The elastic thread has a force constant given by k=mga.
1. Identify the Equilibrium Position:
The equilibrium position occurs when the gravitational force acting on the block is balanced by the elastic force of the thread. At this position, we have:
mg=k⋅x0
where x0 is the extension of the thread at equilibrium.
2. Substituting the Value of k:
We know from the problem that k=mga. Substituting this into the equilibrium equation gives:
mg=(mga)x0
3. Solving for x0:
Rearranging the equation to find x0:
x0=a
4. Calculating Work Done by Gravity:
When the block falls from its initial position to the equilibrium position, the work done by gravity (Wg) is given by:
Wg=mg⋅x0=mg⋅a
5. Calculating the Work Done on the Thread:
The work done on the elastic thread when it stretches from its natural length to the equilibrium position is given by:
Wthread=12kx20
Substituting k and x0:
Wthread=12(mga)a2=12mga
6. Applying the Work-Energy Principle:
The total work done on the block is equal to the change in kinetic energy (KE) as it passes through the equilibrium position:
Wg−Wthread=KE
Substituting the values we found:
mga−12mga=KE
Simplifying this gives:
KE=12mga
Final Answer:
The kinetic energy of the block when it passes through the equilibrium position is:
KE=12mga
The equilibrium position occurs when the gravitational force acting on the block is balanced by the elastic force of the thread. At this position, we have:
mg=k⋅x0
where x0 is the extension of the thread at equilibrium.
We know from the problem that k=mga. Substituting this into the equilibrium equation gives:
mg=(mga)x0
Rearranging the equation to find x0:
x0=a
When the block falls from its initial position to the equilibrium position, the work done by gravity (Wg) is given by:
Wg=mg⋅x0=mg⋅a
The work done on the elastic thread when it stretches from its natural length to the equilibrium position is given by:
Wthread=12kx20
Substituting k and x0:
Wthread=12(mga)a2=12mga
The total work done on the block is equal to the change in kinetic energy (KE) as it passes through the equilibrium position:
Wg−Wthread=KE
Substituting the values we found:
mga−12mga=KE
Simplifying this gives:
KE=12mga
The kinetic energy of the block when it passes through the equilibrium position is:
KE=12mga
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block of mass m is connected to a spring of force constant k. Initially the block is at rest and the spring has natural length. A constant force F is applied hrizontally towards right. The maximum speed of the block will be (there is no friction between block and the surface)

View SolutionA block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).

View SolutionIn the string mass system shown in the figure, the string is compressed by x0=mg2k from its natural length and block is relased from rest. Find the speed o the block when it passes through P (mg/4k distance from mean position)
_S01_030_Q01.png)
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
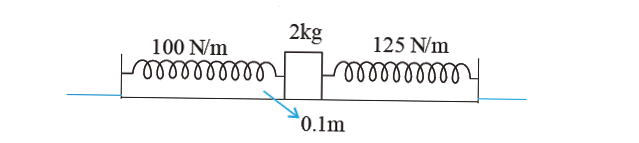
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionA block of mass 10 kg is hanging over a smooth and light pulley through a light string and the other end of the string is pulled down by a constant force F. The kinetic energy of the block increases by 20 J in 1 s
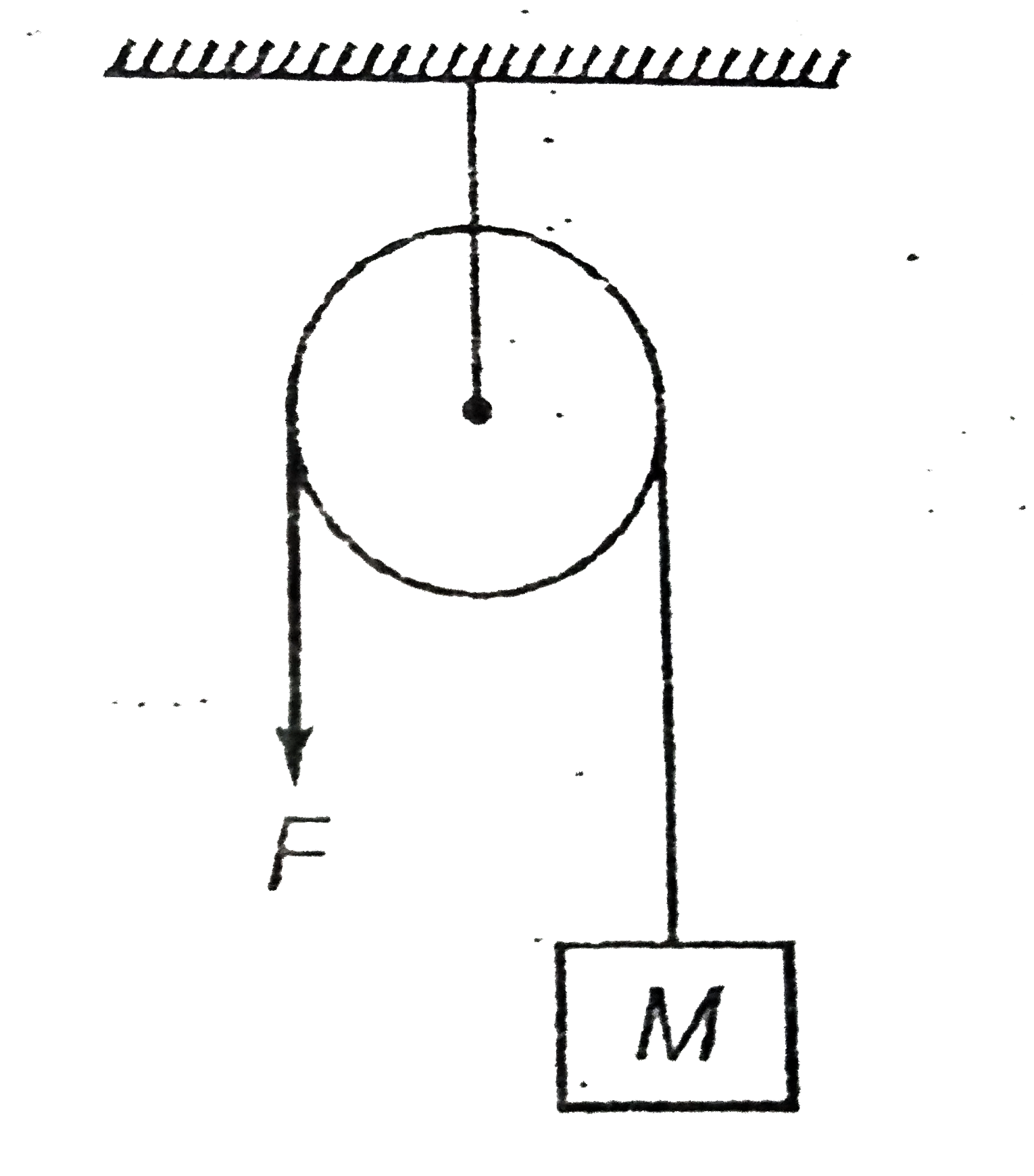
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution
