A block of mass m is attached with a spring in vertical plane as shown in the figure. If initially spring is in its natural length and the block is released from rest, then maximum extension in the spring will be
2mgk
4mgk
mgk
mg2k
The correct Answer is:A
To find the maximum extension of the spring when a block of mass m is attached to it and released from rest, we can follow these steps:
Step 1: Understand the system
The block is initially at rest, and the spring is at its natural length. When the block is released, it will fall under the influence of gravity, and the spring will stretch as the block moves downward.
Step 2: Define the energies involved
At the maximum extension x of the spring, the gravitational potential energy lost by the block will be equal to the elastic potential energy stored in the spring.
- The gravitational potential energy lost by the block when it falls a distance x is given by:
Ei=mgh=mgx
- The elastic potential energy stored in the spring when it is stretched by x is given by:
Ef=12kx2
Step 3: Set up the energy conservation equation
Since energy is conserved, we can equate the initial gravitational potential energy to the final elastic potential energy:
mgx=12kx2
Step 4: Rearrange the equation
Rearranging the equation gives:
12kx2−mgx=0
This is a quadratic equation in x.
Step 5: Factor the equation
Factoring out x gives:
x(12kx−mg)=0
This gives us two solutions: x=0 (the trivial solution) and:
12kx−mg=0⇒kx=2mg⇒x=2mgk
Step 6: Conclusion
Thus, the maximum extension x of the spring is:
x=2mgk
Final Answer
The maximum extension in the spring will be 2mgk.
---
The block is initially at rest, and the spring is at its natural length. When the block is released, it will fall under the influence of gravity, and the spring will stretch as the block moves downward.
At the maximum extension x of the spring, the gravitational potential energy lost by the block will be equal to the elastic potential energy stored in the spring.
Ei=mgh=mgx
- The elastic potential energy stored in the spring when it is stretched by x is given by:
Ef=12kx2
Since energy is conserved, we can equate the initial gravitational potential energy to the final elastic potential energy:
mgx=12kx2
Rearranging the equation gives:
12kx2−mgx=0
This is a quadratic equation in x.
Factoring out x gives:
x(12kx−mg)=0
This gives us two solutions: x=0 (the trivial solution) and:
12kx−mg=0⇒kx=2mg⇒x=2mgk
Thus, the maximum extension x of the spring is:
x=2mgk
The maximum extension in the spring will be 2mgk.
Similar Questions
Find the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionInitially spring is in natural length and both blocks are in rest condition. Then deter mine
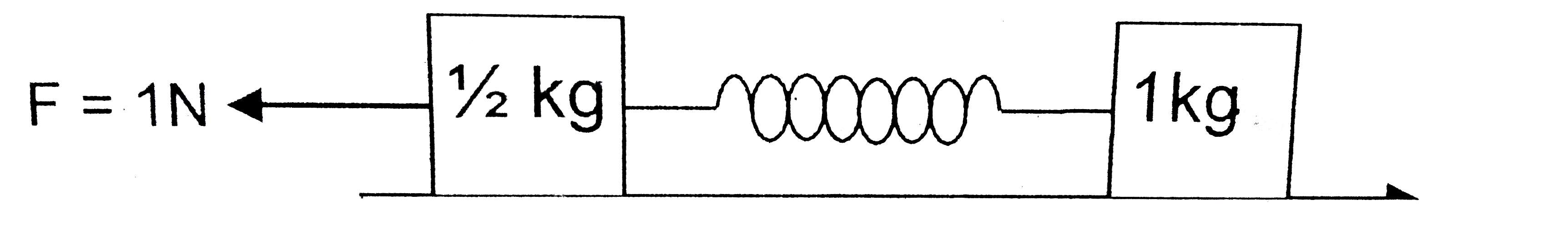
maximum extension in spring . K = 20 N/M
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View SolutionBlock A of mass m is placed on a plank B. A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initially spring is in its natural length. If the plank B is given an acceleration a, then maximum compression in the spring is xmak. Find the value of x (All the surface are smooth)

View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
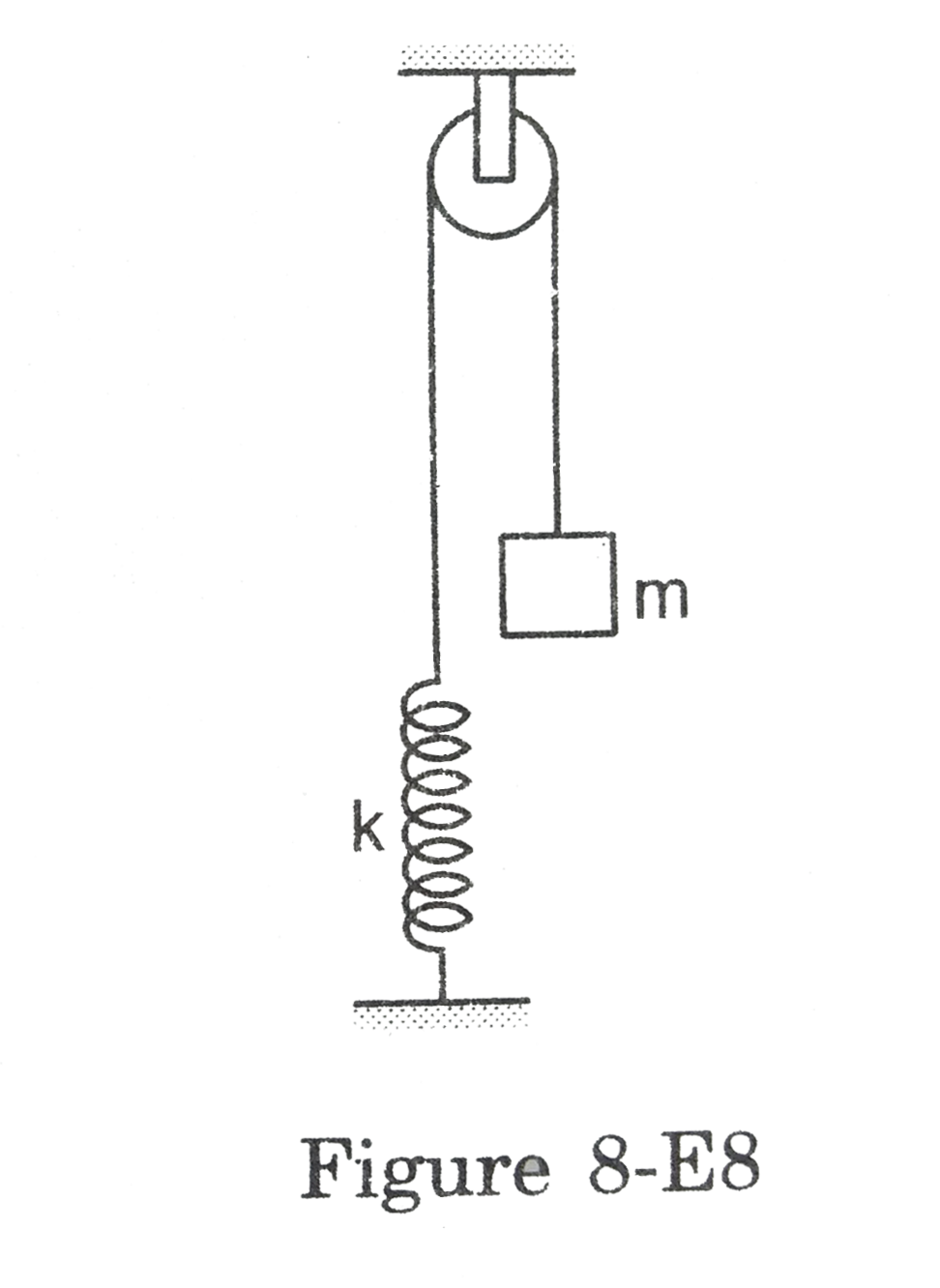
View SolutionConsider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the puley, find the maximum eleongation of the spring.
View SolutionA block is attached to a spring as shown and very-very gradually lowered so that finally spring expands by 'd'. If same block is attached to spring and released suddenly then maximum expansion in spring will be

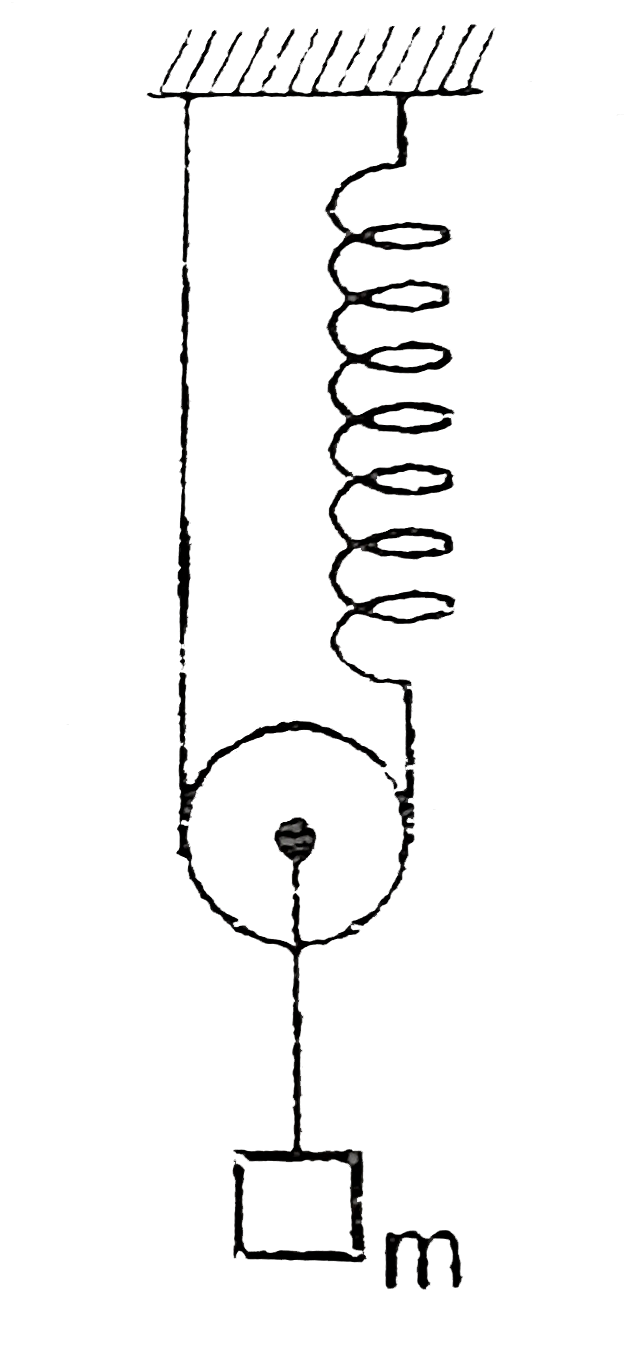
View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
View SolutionThe block is allwed to fall, slowly from the position wher spring is in its natural length. Find, maximum extension in the string.

View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View Solution
