A uniform rod of length l is pivoted at point A. It struk n=by an horizontal force which delivers an ikmpulse J at a distance c from point A as shown in figure. Impulse delivered by pivot is zero, if x is equal to

l2
l3
2l3
3l4
The correct Answer is:C
Step by step video & image solution for A uniform rod of length l is pivoted at point A. It struk n=by an horizontal force which delivers an ikmpulse J at a distance c from point A as shown in figure. Impulse delivered by pivot is zero, if x is equal to by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionA uniform rod of length l is suspended from a point P. and the rod is made to undergo small oxcillations. Match the following
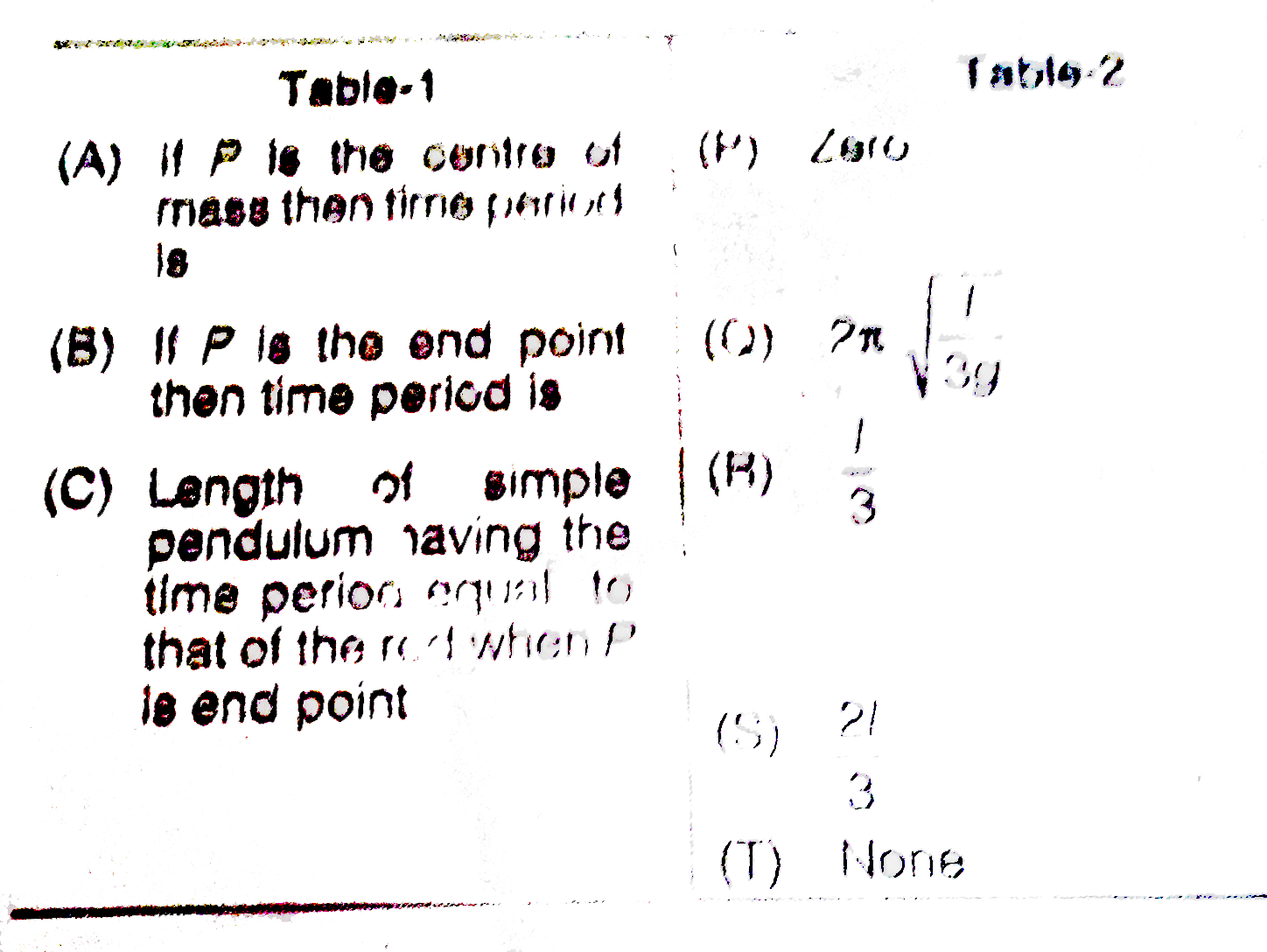
View SolutionA uniform rod of mass m, length l is placed over a smooth horizontal surface along y -axis and is at rest as shown in figure. An impulsive force F is applied for a small time Δt along x-direction at point A. The x-coordinte of end A of the rod when the rod becomes parallel to x-axis for the first is (in itially the coordinates opf centre of mass of the rod is (0,0).

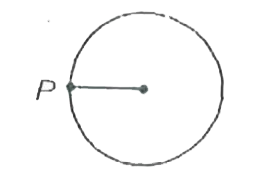
View SolutionA uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle θ is
View SolutionA uniform rod of mass M and length L falls when it is made to stand on a smooth horizontal floor. The trajectories of the points P,Q and R as shown in the figure given below is best represented by :
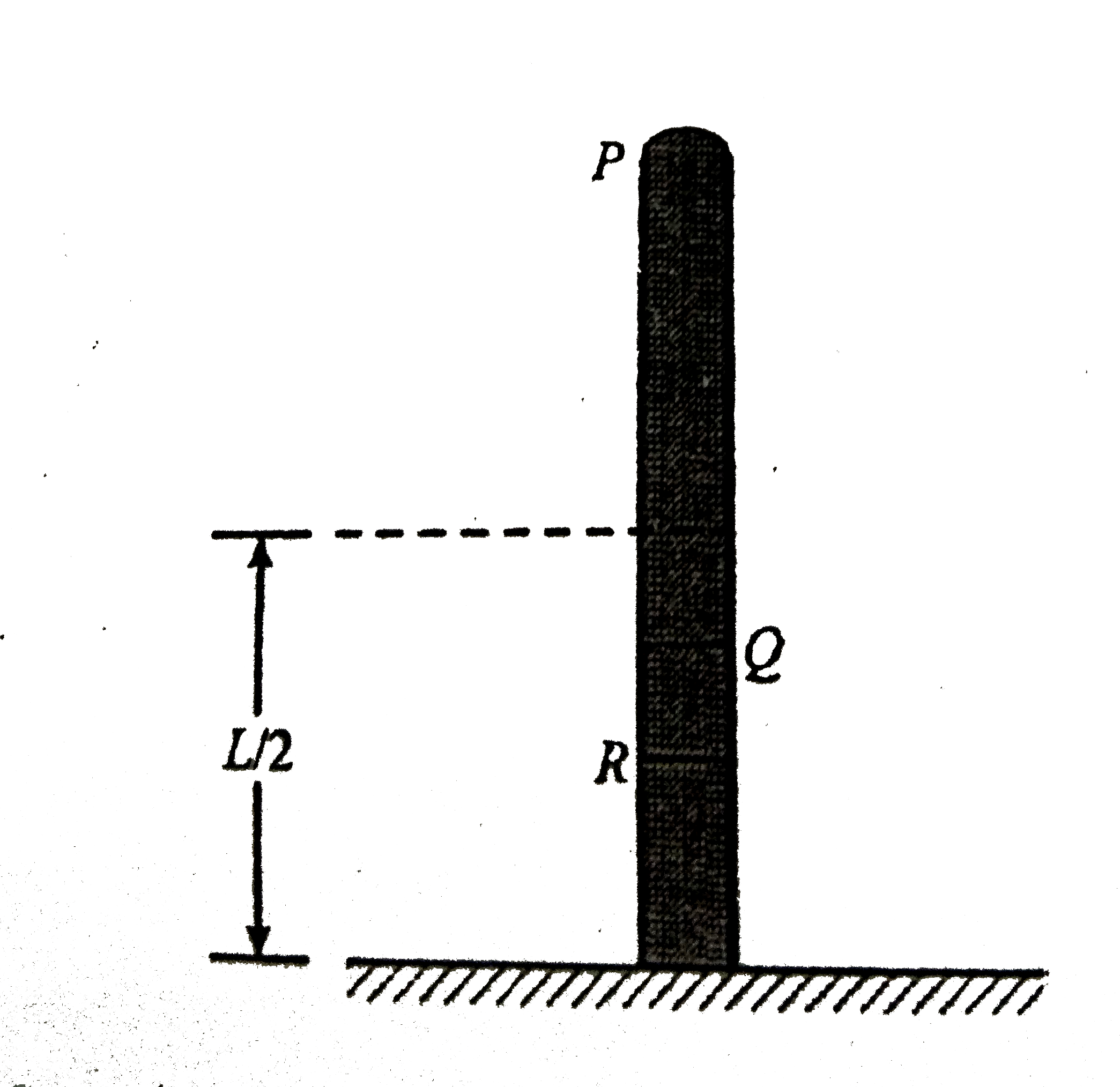
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:


View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

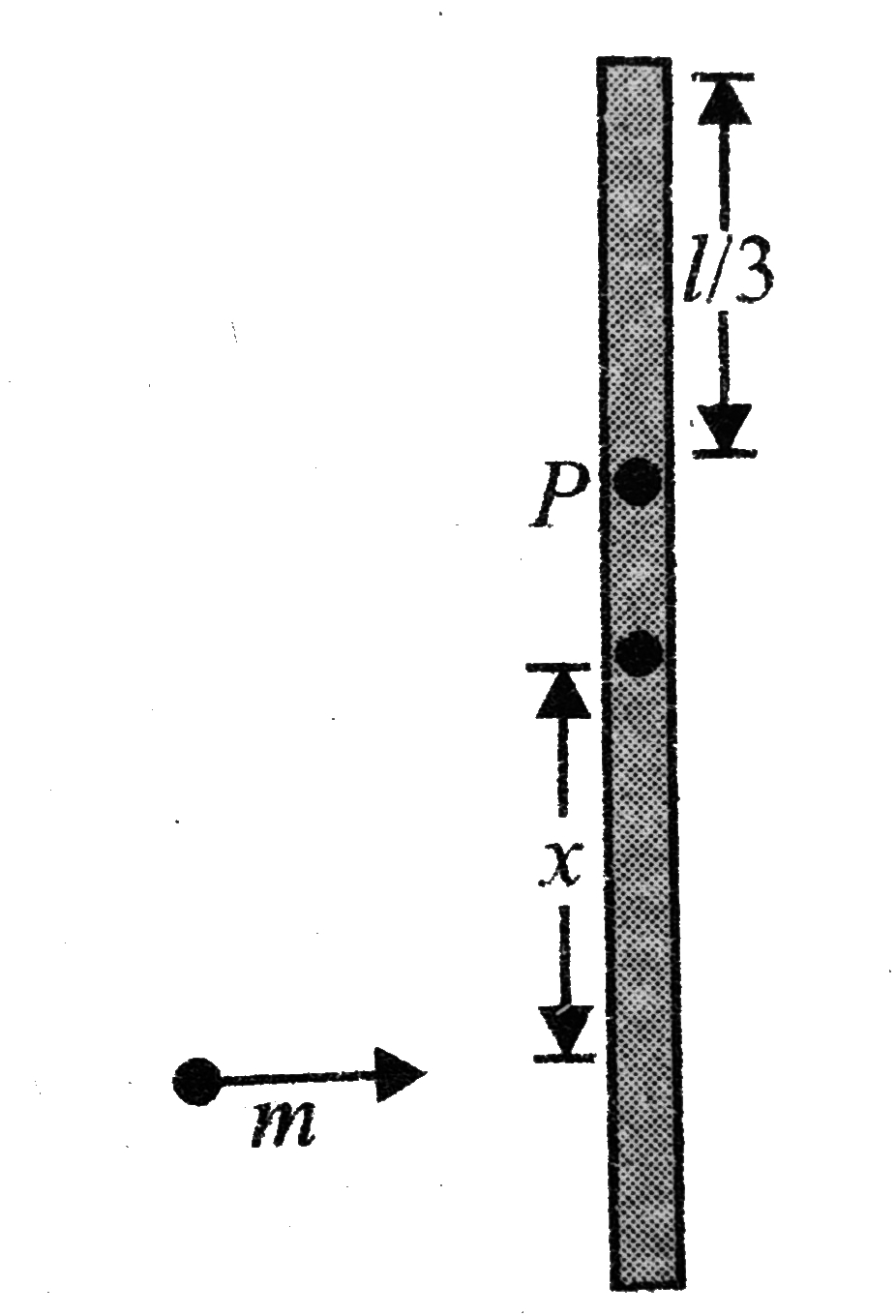
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
View SolutionA thin uniform rod of length l and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)

The distance from the pivot at which impulse, must be applied, if there is to be no horizontal force at the pivot
View SolutionA thin uniform rod of length l and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)

The minimum impulse J required to bring it to rest :
View Solution
