A homogeneous rod of mass 3 kg is pushed along the smooth horizontal surface by a horizontal suface by a horizontal force F equal to 40 N. The angle θ for which rod hasd pure translation motion is (g=10m/s2)
45
∘
37
∘
53
∘
60
∘
45∘
37∘
53∘
60∘
The correct Answer is:B
To solve the problem of determining the angle θ for which the rod has pure translational motion, we can follow these steps:
Step 1: Understand the Forces Acting on the Rod
We have a homogeneous rod of mass m=3kg being pushed by a horizontal force F=40N. The weight of the rod acts downwards and is given by mg, where g=10m/s2.
Step 2: Calculate the Weight of the Rod
The weight W of the rod can be calculated as:
W=mg=3kg×10m/s2=30N
Step 3: Draw the Free Body Diagram
In the free body diagram, we have:
- The force F acting horizontally.
- The normal force N acting vertically upwards.
- The weight W acting vertically downwards.
Step 4: Resolve Forces
When the rod is inclined at an angle θ:
- The horizontal component of the force F is Fcosθ.
- The vertical component of the force F is Fsinθ.
Step 5: Apply Equilibrium Conditions
For pure translational motion, the net torque about the center of mass must be zero. Thus, we can set up the following equations based on the equilibrium of forces and torques.
1. Vertical Forces:
N=mg
2. Horizontal Forces:
The horizontal component of the force must balance the torque due to the weight:
Fsinθ⋅L2=Ncosθ⋅L2
Step 6: Substitute for Normal Force
Substituting N=mg into the torque equation gives:
Fsinθ=mgcosθ
Step 7: Rearranging the Equation
Rearranging the equation gives:
Fmg=cosθsinθ=cotθ
Thus, we can write:
tanθ=mgF
Step 8: Substitute Known Values
Substituting the known values:
tanθ=30N40N=34
Step 9: Find the Angle
To find the angle θ, we can use the inverse tangent function:
θ=tan−1(34)
Using a calculator or trigonometric tables, we find:
θ≈37∘
Conclusion
Thus, the angle θ for which the rod has pure translational motion is:
37∘
We have a homogeneous rod of mass m=3kg being pushed by a horizontal force F=40N. The weight of the rod acts downwards and is given by mg, where g=10m/s2.
The weight W of the rod can be calculated as:
W=mg=3kg×10m/s2=30N
In the free body diagram, we have:
- The force F acting horizontally.
- The normal force N acting vertically upwards.
- The weight W acting vertically downwards.
When the rod is inclined at an angle θ:
- The horizontal component of the force F is Fcosθ.
- The vertical component of the force F is Fsinθ.
For pure translational motion, the net torque about the center of mass must be zero. Thus, we can set up the following equations based on the equilibrium of forces and torques.
N=mg
The horizontal component of the force must balance the torque due to the weight:
Fsinθ⋅L2=Ncosθ⋅L2
Substituting N=mg into the torque equation gives:
Fsinθ=mgcosθ
Rearranging the equation gives:
Fmg=cosθsinθ=cotθ
Thus, we can write:
tanθ=mgF
Substituting the known values:
tanθ=30N40N=34
To find the angle θ, we can use the inverse tangent function:
θ=tan−1(34)
Using a calculator or trigonometric tables, we find:
θ≈37∘
Thus, the angle θ for which the rod has pure translational motion is:
37∘
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A rod of mass m is released on smooth horizontal surface making angle θ with horizontal. Then which of the following statement is correct ?
View SolutionA body of mass 5 kg is at rest on a smooth horizontal surface. A horizontal force 'F' acts on it for 4s and then ceases to act. If the body travels 40 m in the next 5s, the value of F is,
View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View SolutionConsider a block of mass 10kg. which rests on as smooth surface and is subjected to a horizontal force of 6N. If observer A is in a fixed frame x.
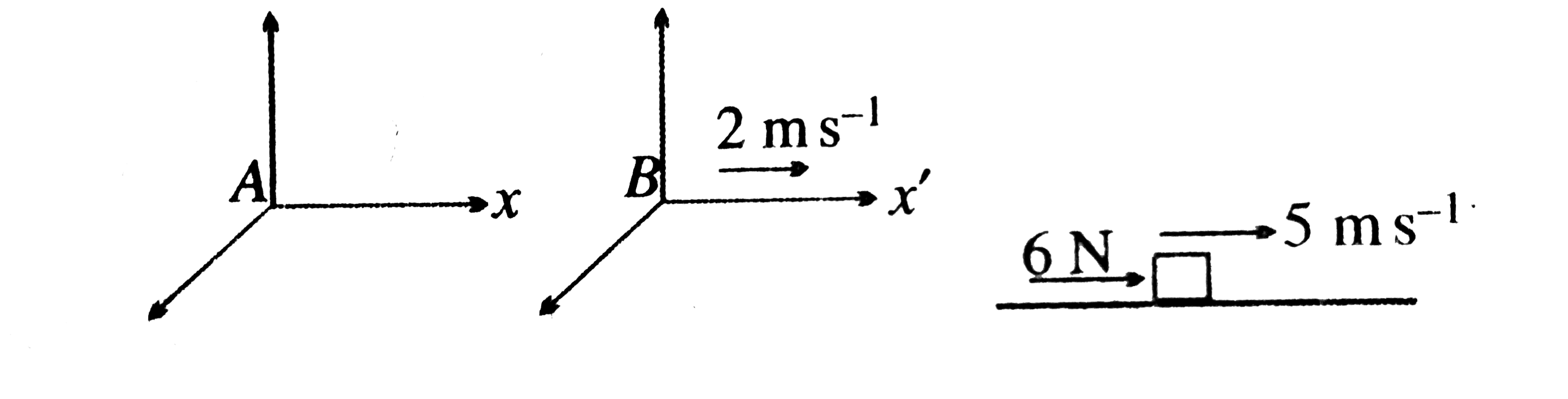
View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:

acceleration of the CM (in ms2)
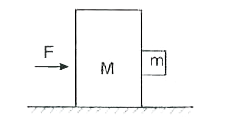
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
View SolutionAn object of mass M and radius R is performing pure rolling motion on a smooth horizontal surface under the action of a constant force F as shown in Fig. The object may be

View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
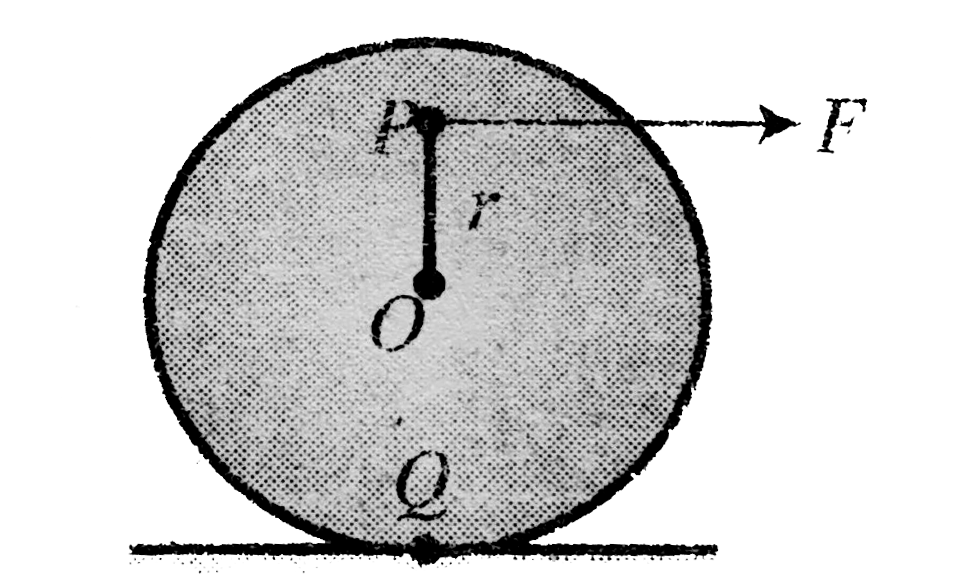
angular acceleration of the disc. (rads−1)
View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View SolutionTwo masses m1 and m2 are placed on a smooth horizontal surface and are connected by a string of negligible mass. A horizontal force F is applied on the mass m2 as shown in the figure. The tension in the string is

View Solution
