A uniform solid cylinder of mass 5kg and radius 0.1m is resting on a horizontal platform (parallel to the x-y plane) and is free to rotate about its axis along the y-axis the platform is given a motion in the x direction given by x=0.2 cos (10t) m if there is no slipping then maximum torque acting on the cylinder during its motion is
0.2N−m
2.0N−m
5.0N−m
10.0N−m
The correct Answer is:C
To find the maximum torque acting on the cylinder during its motion, we can follow these steps:
Step 1: Understand the motion of the platform
The platform moves in the x-direction according to the equation:
x(t)=0.2cos(10t)
Step 2: Find the velocity of the cylinder
To find the velocity of the cylinder, we differentiate the position with respect to time:
v(t)=dxdt=−0.2⋅10sin(10t)=−2sin(10t)m/s
Step 3: Find the acceleration of the cylinder
Next, we differentiate the velocity to find the acceleration:
a(t)=dvdt=−2⋅10cos(10t)=−20cos(10t)m/s2
Step 4: Determine the maximum acceleration
The maximum value of a(t) occurs when cos(10t)=1:
amax=20m/s2
Step 5: Relate torque to angular acceleration
The torque τ acting on the cylinder is given by:
τ=Iα
where I is the moment of inertia and α is the angular acceleration. For a solid cylinder, the moment of inertia I is:
I=12mr2
where m=5kg and r=0.1m.
Step 6: Calculate the moment of inertia
Substituting the values:
I=12×5×(0.1)2=12×5×0.01=0.025kg m2
Step 7: Relate linear acceleration to angular acceleration
Since there is no slipping, we have:
a=αr
Thus, the angular acceleration α can be expressed as:
α=ar=200.1=200rad/s2
Step 8: Calculate the maximum torque
Now we can calculate the maximum torque:
τmax=Iα=0.025×200=5N m
Final Answer
The maximum torque acting on the cylinder during its motion is:
τmax=5N m
---
The platform moves in the x-direction according to the equation:
x(t)=0.2cos(10t)
To find the velocity of the cylinder, we differentiate the position with respect to time:
v(t)=dxdt=−0.2⋅10sin(10t)=−2sin(10t)m/s
Next, we differentiate the velocity to find the acceleration:
a(t)=dvdt=−2⋅10cos(10t)=−20cos(10t)m/s2
The maximum value of a(t) occurs when cos(10t)=1:
amax=20m/s2
The torque τ acting on the cylinder is given by:
τ=Iα
where I is the moment of inertia and α is the angular acceleration. For a solid cylinder, the moment of inertia I is:
I=12mr2
where m=5kg and r=0.1m.
Substituting the values:
I=12×5×(0.1)2=12×5×0.01=0.025kg m2
Since there is no slipping, we have:
a=αr
Thus, the angular acceleration α can be expressed as:
α=ar=200.1=200rad/s2
Now we can calculate the maximum torque:
τmax=Iα=0.025×200=5N m
The maximum torque acting on the cylinder during its motion is:
τmax=5N m
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A cylinder of mass M and radius R is resting on a horizontal platform (which is parallel to the x-y plane) with its axis fixed along the y-axis and free to rotate about its axis. The platform is given a motion in the x-direction given by x=Acos(ωt). There is no slipping between the cylinder and platform. The maximum torque acting on the cylinder during its motion is ..................
View SolutionA solid cylinder of mass 2 kg and radius 4 cm rotating about its axis at the rate of 3 rpm. The torque required to stop after 2π revolutions is :
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A cylinder of mass 5kg and radius 10cm is moving on a horizontal surface with speed. 5m/s and angular speed about axis through C.M.10rad/s. Find the angular momentum of the cylinder about point of contact.
View SolutionA particle of mass m is moving along a trajectory given by
x=x0+acosω1t
y=y0+bsinω2t
The torque, acting on the particle about the origin, at t=0 is:
View SolutionA soild cylinder of mass 2 kg and radius 0.2 m is rotating about its owm axis without friction with an angular velocity of 3 rad s−1 . Angular momentum of the cylinder is
View SolutionA solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
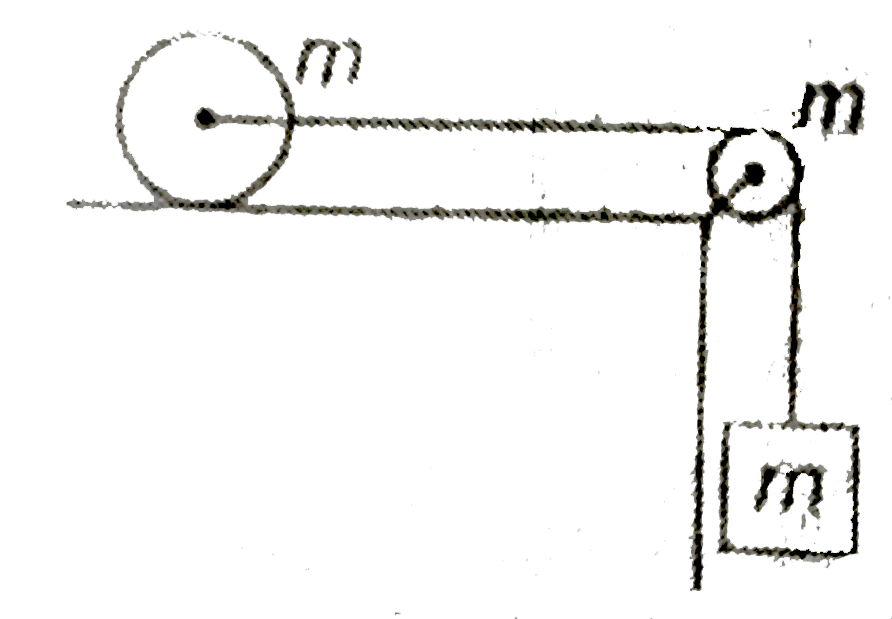
Force of friction acting on the cylinder is
View SolutionA uniform solid cylinder of mass m and radius 2R rests on a horizontal table. A string attached to it passes over a pulley (disc) of mass m and radius R that is mounted on a fricitonaless axle through its centre . A block of mass m is suspended from the free end of the spring . The string does not slip over the pulley surface and the cylinder rolls without slipping on the table.
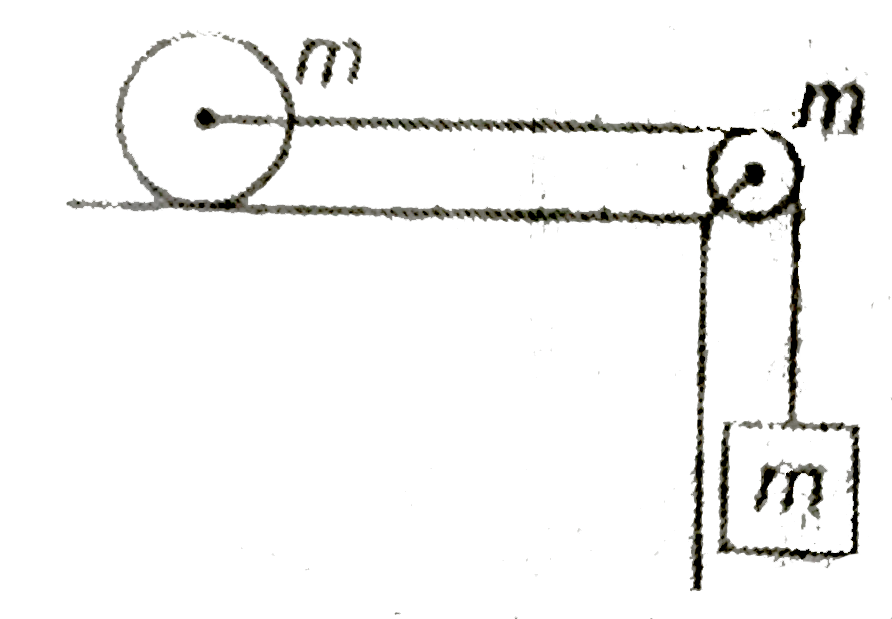
Angular acceleration of the cylinder is
View SolutionA uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
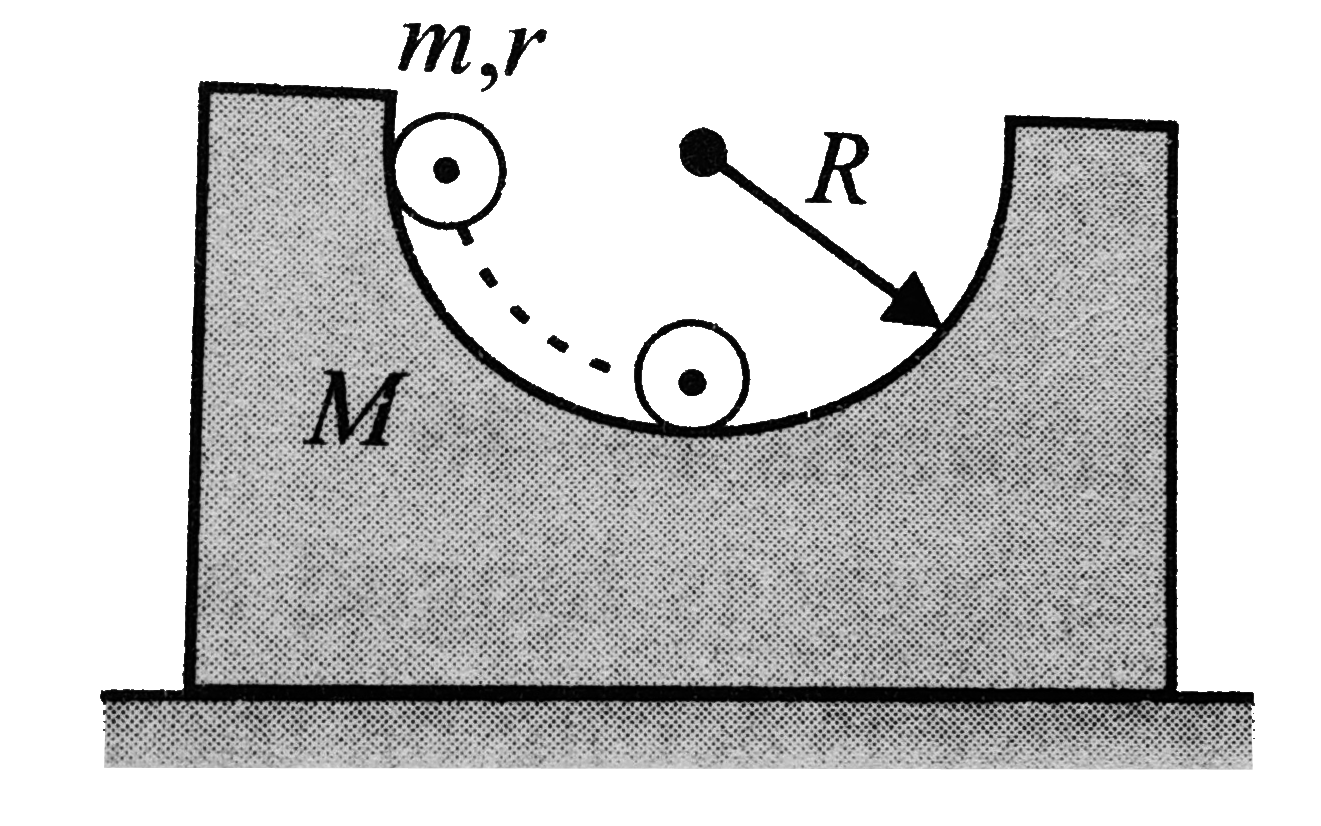
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is
View Solution
