A disc can roll wihtout slippingg, without applying any external force on a
(a)rough inclined plane
smooth inclined plane
(c)rough horizontal surface
(d)smooth horizontal surface
The correct Answer is:A, C, D
It seems that the provided transcript is not related to the question about a disc rolling without slipping. However, I will provide a step-by-step solution to the question regarding the rolling disc.
1. Understanding the Concept of Rolling Without Slipping:
- A disc rolls without slipping when the point of contact with the ground does not slide. This means that the linear velocity of the center of mass (v) is related to the angular velocity (ω) by the equation:
v=R⋅ω
where R is the radius of the disc.
2. Identifying Forces and Motion:
- When a disc rolls down an incline or on a flat surface without any external force, it experiences gravitational force acting downwards and the normal force acting perpendicular to the surface. The frictional force at the point of contact prevents slipping.
3. Using Energy Conservation:
- The total mechanical energy of the disc is conserved when rolling without slipping. The potential energy (PE) at the height is converted into kinetic energy (KE) as it rolls down:
PE=KEtranslational+KErotational
- The translational kinetic energy is given by:
KEtranslational=12mv2
- The rotational kinetic energy is given by:
KErotational=12Iω2
- For a solid disc, the moment of inertia I is:
I=12mR2
4. Relating Linear and Angular Velocities:
- Substitute ω in terms of v:
ω=vR
- Therefore, the rotational kinetic energy becomes:
KErotational=12(12mR2)(vR)2=14mv2
5. Setting Up the Energy Equation:
- The total kinetic energy when rolling without slipping is:
KEtotal=KEtranslational+KErotational=12mv2+14mv2=34mv2
- Setting the potential energy equal to the total kinetic energy:
mgh=34mv2
- The mass m cancels out:
gh=34v2
6. Solving for Linear Velocity:
- Rearranging the equation to solve for v:
v2=4gh3
v=√4gh3
Final Result:
The linear velocity v of the disc rolling without slipping is given by:
v=√4gh3
- A disc rolls without slipping when the point of contact with the ground does not slide. This means that the linear velocity of the center of mass (v) is related to the angular velocity (ω) by the equation:
v=R⋅ω
where R is the radius of the disc.
- When a disc rolls down an incline or on a flat surface without any external force, it experiences gravitational force acting downwards and the normal force acting perpendicular to the surface. The frictional force at the point of contact prevents slipping.
- The total mechanical energy of the disc is conserved when rolling without slipping. The potential energy (PE) at the height is converted into kinetic energy (KE) as it rolls down:
PE=KEtranslational+KErotational
- The translational kinetic energy is given by:
KEtranslational=12mv2
- The rotational kinetic energy is given by:
KErotational=12Iω2
- For a solid disc, the moment of inertia I is:
I=12mR2
- Substitute ω in terms of v:
ω=vR
- Therefore, the rotational kinetic energy becomes:
KErotational=12(12mR2)(vR)2=14mv2
- The total kinetic energy when rolling without slipping is:
KEtotal=KEtranslational+KErotational=12mv2+14mv2=34mv2
- Setting the potential energy equal to the total kinetic energy:
mgh=34mv2
- The mass m cancels out:
gh=34v2
- Rearranging the equation to solve for v:
v2=4gh3
v=√4gh3
The linear velocity v of the disc rolling without slipping is given by:
v=√4gh3
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
16 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
Can kinetic energy of a system be increased without applying any external force on the system?
View SolutionA particle of mass 'm' is attached to the rim of a uniform disc of mass 'm' and radius R. The disc is rolling wihtout slipping on a stationery horizontal surface as shown in the figure. At a particular instant, the particle is at the topmost position and centre of the disc has speed v0 amd its angular speed is ω. Choose the correct option (s).
View SolutionA disc is rolling without slipping with angular velocity ω. P and Q are two points equidistant from the centre C. the order of magnitude fo velocity is
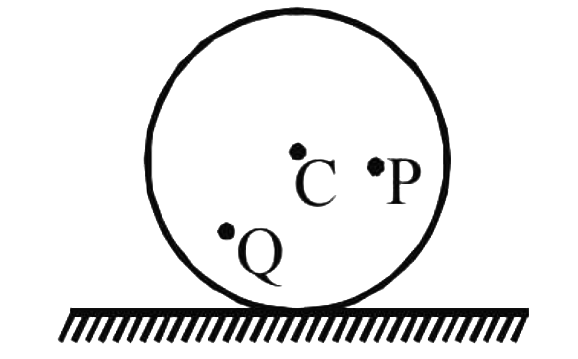
View Solution
A disc is rolling without slipping with linear velocity v as shown in figure. With the concept of instantaneous axis of rotation, find velocities of point A, B, C and D.
View SolutionA : rigid body can't be in a pure rolling on a rough inclined plane without giving any external force.
R : Since there is no torque providing force acting on the body in the above case, the body can't come in a rolling condition.
View SolutionAs shown in the figure, a disc of mass m is rolling without slipping with angular velocity ω. When it crosses point B disc will be in

View SolutionA uniform solid cylindrical roller of mass m and R is rolled on the ground , without slipping , by applying a constant horizontal force F. Find angular acceleration of cylinder .

View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionWhen a body rolls without sliding up an inclined plane the frictional force is :
View SolutionA lawn roller in the form of a thin-walled hollow cylinder of mass M is pulled horizotally with a constant horizontally force F applied by a handle attached to the axle. If it rolls without slipping. Find the acceleration and the friction forces.
View Solution
