Moment of inertia of a straight wire about an axis perpendicular to the wire passing through one of its end is I.
This wire is now framed into a circle (a ring) of single turn. The moment of inertia of this ring about an axis passing through centre and perpendicular to its plane would be
(3π2)l
(34π2)l
(π23)l
(4π23)l
The correct Answer is:B
To solve the problem, we need to find the moment of inertia of a ring formed by bending a straight wire, given that the moment of inertia of the straight wire about an axis perpendicular to it and passing through one of its ends is I.
1. Understand the Moment of Inertia of the Straight Wire:
- The moment of inertia I of the straight wire about an axis perpendicular to it and passing through one of its ends can be expressed as:
I=ML23
where M is the mass of the wire and L is its length.
2. Convert the Straight Wire into a Ring:
- When the straight wire is bent into a ring, the length of the wire remains the same. The circumference of the ring is given by:
C=2πr
where r is the radius of the ring. Setting this equal to the length of the wire:
2πr=L
From this, we can express the radius r in terms of the length L:
r=L2π
3. Find the Moment of Inertia of the Ring:
- The moment of inertia I′ of a ring about an axis passing through its center and perpendicular to its plane is given by:
I′=mr2
where m is the mass of the ring. Since the mass of the wire remains the same, we can use M for m:
I′=Mr2
Substituting the expression for r:
I′=M(L2π)2=ML24π2
4. Relate ML2 to I:
- From the moment of inertia of the straight wire, we have:
ML2=3I
Now, substitute this into the equation for I′:
I′=3I4π2
5. Final Result:
- Therefore, the moment of inertia of the ring about an axis passing through its center and perpendicular to its plane is:
I′=3I4π2
Conclusion:
The moment of inertia of the ring is 3I4π2.
- The moment of inertia I of the straight wire about an axis perpendicular to it and passing through one of its ends can be expressed as:
I=ML23
where M is the mass of the wire and L is its length.
- When the straight wire is bent into a ring, the length of the wire remains the same. The circumference of the ring is given by:
C=2πr
where r is the radius of the ring. Setting this equal to the length of the wire:
2πr=L
From this, we can express the radius r in terms of the length L:
r=L2π
- The moment of inertia I′ of a ring about an axis passing through its center and perpendicular to its plane is given by:
I′=mr2
where m is the mass of the ring. Since the mass of the wire remains the same, we can use M for m:
I′=Mr2
Substituting the expression for r:
I′=M(L2π)2=ML24π2
- From the moment of inertia of the straight wire, we have:
ML2=3I
Now, substitute this into the equation for I′:
I′=3I4π2
- Therefore, the moment of inertia of the ring about an axis passing through its center and perpendicular to its plane is:
I′=3I4π2
The moment of inertia of the ring is 3I4π2.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
16 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
Moment of inertia of a straight wire about an axis perpendicular to the wire passing through one of its end is I.
Now the same wire is bent into a ring of two turns , then the moment of inertia would be
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe mass of a uniform circular ring of radius 0.2m is 0.1kg. Calcuate the moment of inertia of the ring about an axis passing through its centre an perpendicular to its surface.
View SolutionThe moment of inertia of ring about an axis passing through its diameter is I. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View SolutionThe mass of a uniform circular ring of radius 0.2m is 0.1kg. Calculate the moment of inertia of the ring about an axis passing through its center and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
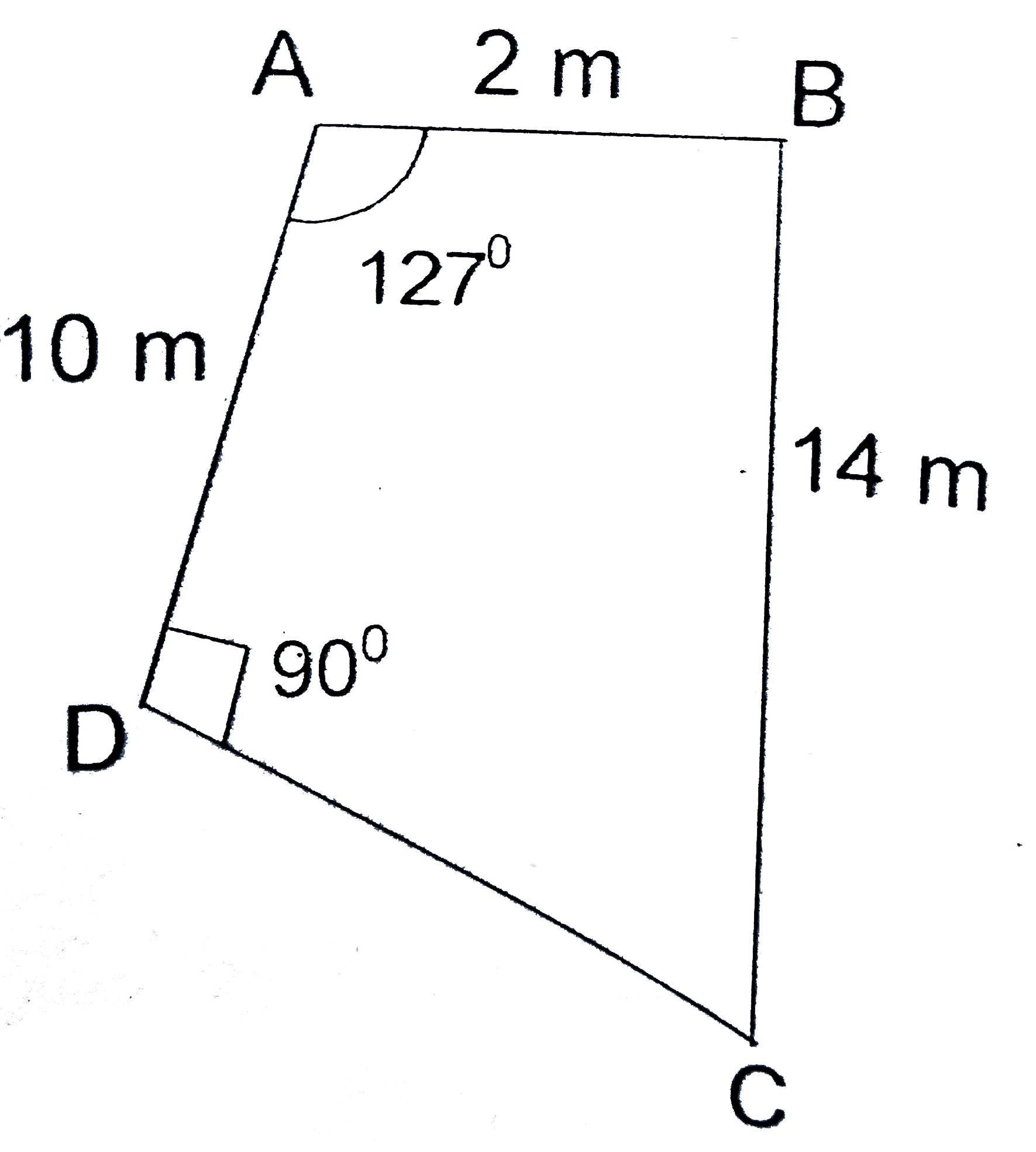
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View Solution
