A ball B of mass m is lying at rest on the top surface of a smooth horizontal table 5 m high. Another moovin ball A of same mass make an elastic colision with B slides off the table and strikes the floor at a horizonatal distance of 10 m from the table. Then select the correct alternatives (s). [g=10m/s2]
The velocity of the ball A befor collisionis 5 m/s
The kinetic energy of the ball B at the time when it strikes yhe ground is (mx100) J
the velocity of the ball A before collision is 10 m/s
The kinetic energy of the ball B at the time when it strikes the ground is (50xm) J
The correct Answer is:C,D
To solve the problem, we will analyze the situation step by step.
Step 1: Understanding the Problem
We have two balls, A and B, both with mass m. Ball B is at rest on a table that is 5 meters high. Ball A is moving and collides elastically with ball B, causing ball B to remain at rest and ball A to slide off the table.
Step 2: Determine the Velocity of Ball A Before Collision
Since the collision is elastic and both balls have the same mass, we can use the conservation of momentum and kinetic energy. After the collision, ball A will move with the same velocity that ball B had before the collision.
Using the conservation of energy:
12mv2=mgh
Where:
- h=5m
- g=10m/s2
Rearranging gives:
v2=2gh
Substituting the values:
v2=2×10×5=100
Taking the square root:
v=√100=10m/s
Thus, the velocity of ball A before the collision is 10m/s.
Step 3: Analyzing the Motion of Ball A After Collision
After the collision, ball A slides off the table horizontally. We need to find the time it takes for ball A to hit the ground.
Using the formula for the time of free fall:
h=12gt2
Substituting h=5m and g=10m/s2:
5=12×10×t2
This simplifies to:
5=5t2⟹t2=1⟹t=1s
Step 4: Finding the Horizontal Distance
Now, we can calculate the horizontal distance traveled by ball A while it is falling. The horizontal distance d can be calculated using:
d=v×t
Where:
- v=10m/s
- t=1s
Substituting the values:
d=10×1=10m
Step 5: Conclusion
The horizontal distance from the table to where ball A strikes the ground is indeed 10m, which matches the information provided in the problem.
Final Answers
1. The velocity of ball A before the collision is 10m/s.
2. The time taken for ball A to hit the ground is 1s.
3. The horizontal distance traveled by ball A is 10m.
We have two balls, A and B, both with mass m. Ball B is at rest on a table that is 5 meters high. Ball A is moving and collides elastically with ball B, causing ball B to remain at rest and ball A to slide off the table.
Since the collision is elastic and both balls have the same mass, we can use the conservation of momentum and kinetic energy. After the collision, ball A will move with the same velocity that ball B had before the collision.
12mv2=mgh
Where:
- h=5m
- g=10m/s2
v2=2gh
Substituting the values:
v2=2×10×5=100
Taking the square root:
v=√100=10m/s
Thus, the velocity of ball A before the collision is 10m/s.
After the collision, ball A slides off the table horizontally. We need to find the time it takes for ball A to hit the ground.
h=12gt2
Substituting h=5m and g=10m/s2:
5=12×10×t2
This simplifies to:
5=5t2⟹t2=1⟹t=1s
Now, we can calculate the horizontal distance traveled by ball A while it is falling. The horizontal distance d can be calculated using:
d=v×t
Where:
- v=10m/s
- t=1s
d=10×1=10m
The horizontal distance from the table to where ball A strikes the ground is indeed 10m, which matches the information provided in the problem.
1. The velocity of ball A before the collision is 10m/s.
2. The time taken for ball A to hit the ground is 1s.
3. The horizontal distance traveled by ball A is 10m.
Similar Questions
A ball A collides elasticlly with an another identical bass B with velocity 10 m//s at an angle of 30∘ from the line joining their centres C1 and C2 Select the correct alternative (s).
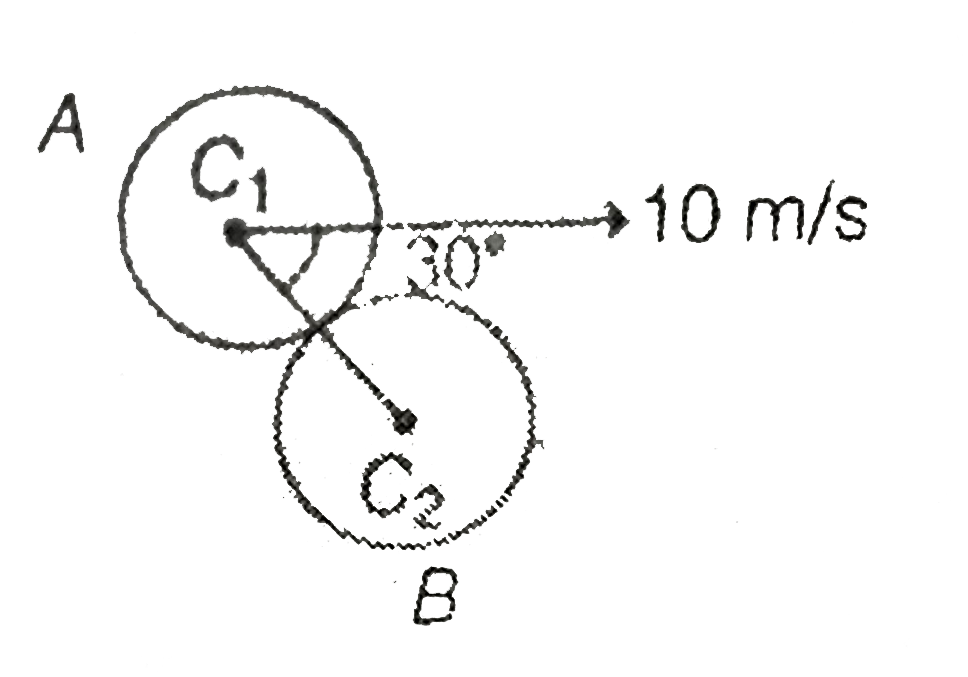
View SolutionA uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at 60∘ to AC.
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA ball rolls off the edge of a horizontal table top 4 m high. If it strikes the floor at a point 5 m horizontally away from the edge of the table, what was its speed at the instant it left the table?
View SolutionA ball of mass 2kg is thrown with velocity 10ms at an angle of 30°to the horizontal and another ball with the same mass is thrown at an angel of 60° to the horizontal with the same speed.The ratio will be their range will be
View SolutionThe sides of rectangular plate of mass 20 kg is 5 m x 4 m placed on a horizontal table. The pressure exerted by the block on the table is (Take g=10ms2)
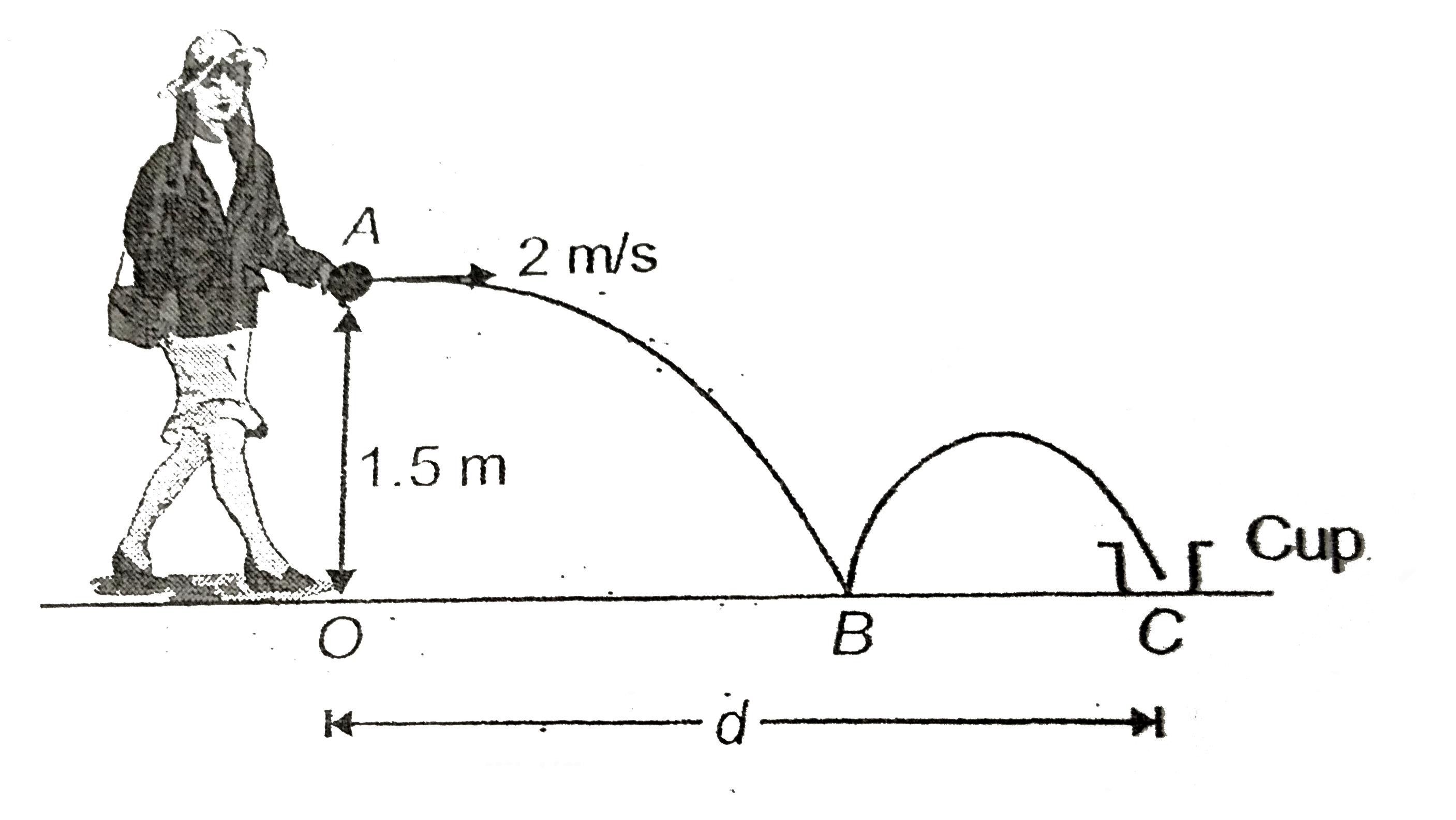
View SolutionA girl throws the ball with horizontal velocity 2m/s at the moment t=0. The ball bounces once on the smooth floor and then lands into cup C. The coefficient of restitution for the collision is 0.8. Select the correct alternative (g=10m/s2)
View SolutionA ball of mass 4 kg moving on a smooth horizontal surface makes an elastic collision with another ball of mass m at rest in the line of motion of first ball. If after collision first ball moves in the same direction with one fourth of its velocity before collision, then mass of second ball is
View Solution
