A cubical block of wood of specific gravity 0.5 and chunk of concrete of specific gravity 2.5 are fastened together. the ratio of mass of wood to the mass of concrete which makes the combination to float with entire volume of the combination submerged in water is
53
65
52
43
The correct Answer is:A
To solve the problem, we need to find the ratio of the mass of wood to the mass of concrete when they are fastened together and completely submerged in water.
1. Understanding Specific Gravity:
- Specific gravity (SG) is defined as the ratio of the density of a substance to the density of water.
- For wood, SG = 0.5, which means its density ρwood=0.5×ρwater.
- For concrete, SG = 2.5, which means its density ρconcrete=2.5×ρwater.
2. Let Volumes be Defined:
- Let the volume of wood be V1 and the volume of concrete be V2.
3. Weight of the System:
- The total weight of the system (wood + concrete) is given by:
W=mwood+mconcrete=ρwood⋅V1+ρconcrete⋅V2
4. Buoyant Force:
- The buoyant force acting on the submerged object is equal to the weight of the water displaced by the total volume V1+V2:
Fb=ρwater⋅g⋅(V1+V2)
5. Equating Weight and Buoyant Force:
- For the combination to float with the entire volume submerged, the weight of the system must equal the buoyant force:
ρwood⋅V1+ρconcrete⋅V2=ρwater⋅(V1+V2)
6. Substituting Densities:
- Substitute the densities in terms of specific gravity:
(0.5⋅ρwater)⋅V1+(2.5⋅ρwater)⋅V2=ρwater⋅(V1+V2)
- Dividing through by ρwater:
0.5V1+2.5V2=V1+V2
7. Rearranging the Equation:
- Rearranging gives us:
0.5V1+2.5V2−V1−V2=0
−0.5V1+1.5V2=0
1.5V2=0.5V1
V1V2=1.50.5=3
8. Finding the Mass Ratio:
- The mass of wood mwood=ρwood⋅V1=(0.5⋅ρwater)⋅V1
- The mass of concrete mconcrete=ρconcrete⋅V2=(2.5⋅ρwater)⋅V2
- The ratio of mass of wood to mass of concrete is:
mwoodmconcrete=(0.5⋅ρwater)⋅V1(2.5⋅ρwater)⋅V2=0.5⋅V12.5⋅V2
- Substituting V1V2=3:
mwoodmconcrete=0.5⋅32.5=1.52.5=35
Final Answer:
The ratio of the mass of wood to the mass of concrete is 35.
- Specific gravity (SG) is defined as the ratio of the density of a substance to the density of water.
- For wood, SG = 0.5, which means its density ρwood=0.5×ρwater.
- For concrete, SG = 2.5, which means its density ρconcrete=2.5×ρwater.
- Let the volume of wood be V1 and the volume of concrete be V2.
- The total weight of the system (wood + concrete) is given by:
W=mwood+mconcrete=ρwood⋅V1+ρconcrete⋅V2
- The buoyant force acting on the submerged object is equal to the weight of the water displaced by the total volume V1+V2:
Fb=ρwater⋅g⋅(V1+V2)
- For the combination to float with the entire volume submerged, the weight of the system must equal the buoyant force:
ρwood⋅V1+ρconcrete⋅V2=ρwater⋅(V1+V2)
- Substitute the densities in terms of specific gravity:
(0.5⋅ρwater)⋅V1+(2.5⋅ρwater)⋅V2=ρwater⋅(V1+V2)
- Dividing through by ρwater:
0.5V1+2.5V2=V1+V2
- Rearranging gives us:
0.5V1+2.5V2−V1−V2=0
−0.5V1+1.5V2=0
1.5V2=0.5V1
V1V2=1.50.5=3
- The mass of wood mwood=ρwood⋅V1=(0.5⋅ρwater)⋅V1
- The mass of concrete mconcrete=ρconcrete⋅V2=(2.5⋅ρwater)⋅V2
- The ratio of mass of wood to mass of concrete is:
mwoodmconcrete=(0.5⋅ρwater)⋅V1(2.5⋅ρwater)⋅V2=0.5⋅V12.5⋅V2
- Substituting V1V2=3:
mwoodmconcrete=0.5⋅32.5=1.52.5=35
The ratio of the mass of wood to the mass of concrete is 35.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
wood with specific gravity of less than 0.2 is
View SolutionA block B of specific gravity 2 and another block C of specific gravity 0.5 .Both are joined together and they are floating water such that they are completely dipped inside water , the ratio of the masses of the blocks B and C is
View SolutionA block of wood weighing 71.2N and of specific gravity 0.75 is tied by a string to the bottom of a tank of water in order to have the block totally immersed, What is the tension in the string?
View SolutionA block of wood of mass 24 kg floats in water. The volume of wood is 0.032 m. Find the volume of block below the surface of water
View SolutionA cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block of float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
View SolutionA block of wood has a mass of 25g. When a 5g metal piece with a volume of 2cm3 is attached to the bottom of the block, the wood barely floats in water. What is the volume V of the wood?
View SolutionA small block of wood of specific gravity 0.5 is subnerged at a depth of 1.2 m in a vessel filled with water. The vessel is accelerated upwards with an acceleration a0=g2. Time taken by the block to reach the surface, if it is released with zero initial velocity is (g=10m/s2)
View SolutionA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
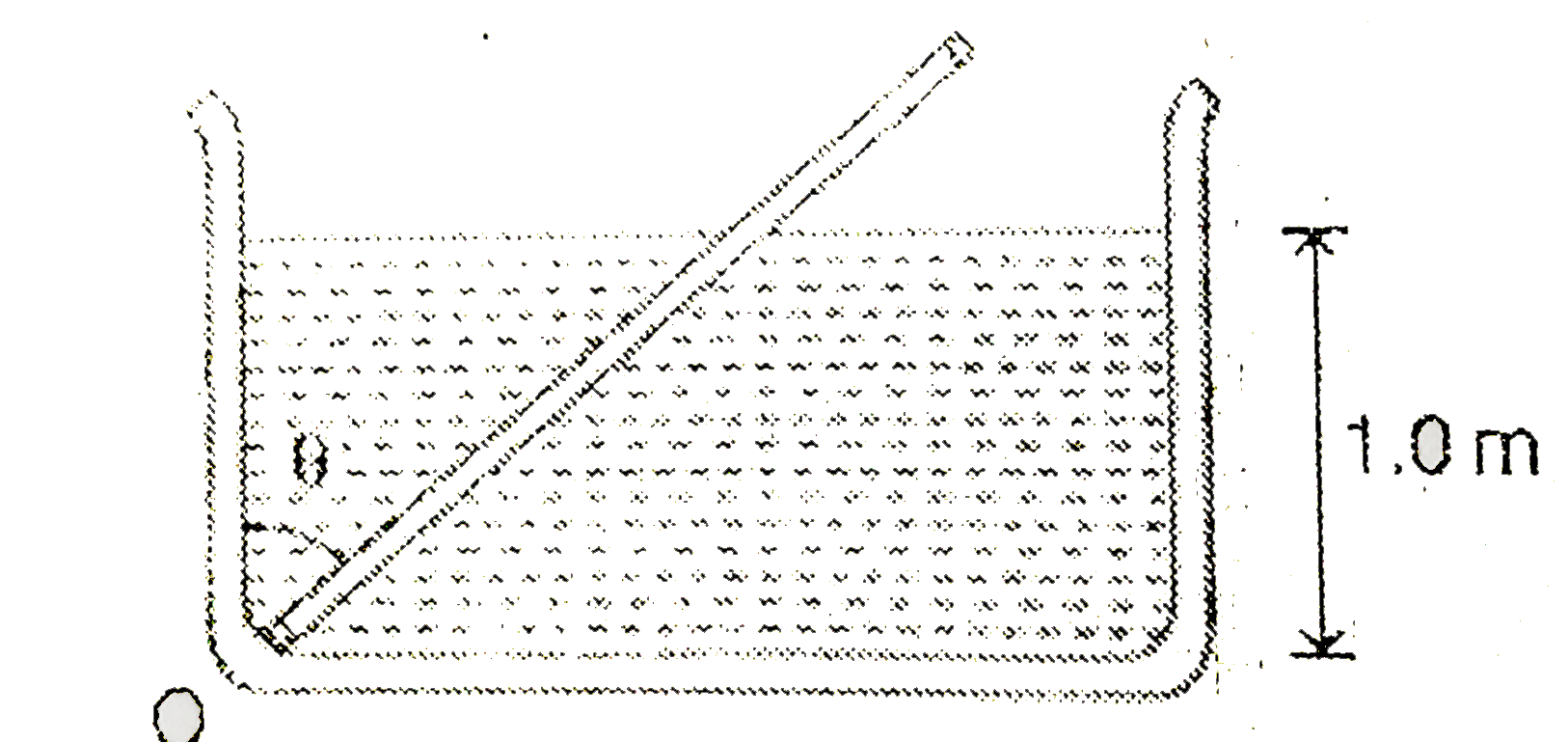
View SolutionA solution of acid having 62% by mass of acid has specific gravity of 1.8 g. If the solution is to be diluted to attain a specific gravity of 1.2 then what volume of water should be added to 100 ml of this solution?
View Solution
