A small block of wood of specific gravity 0.5 is subnerged at a depth of 1.2 m in a vessel filled with water. The vessel is accelerated upwards with an acceleration a0=g2. Time taken by the block to reach the surface, if it is released with zero initial velocity is (g=10m/s2)
0.6 s
0.4 s
1.2 s
1 s
The correct Answer is:B
To solve the problem, we need to determine the time taken by a small block of wood with a specific gravity of 0.5 to reach the surface of a water-filled vessel that is accelerating upwards with an acceleration of a0=g2. The block is submerged at a depth of 1.2 m and is released from rest.
1. Understand the Given Data:
- Specific gravity of the block, SG=0.5
- Depth of the block, h=1.2m
- Acceleration due to gravity, g=10m/s2
- Upward acceleration of the vessel, a0=g2=5m/s2
2. Calculate the Weight and Buoyant Force:
- The weight of the block W=m⋅g
- The volume of the block V=mρwood where ρwood=SG⋅ρwater=0.5⋅1000kg/m3=500kg/m3
- The buoyant force Fb=ρwater⋅V⋅g=1000⋅m500⋅g=2m⋅g
3. Determine the Net Acceleration of the Block:
- The net force acting on the block when the vessel is accelerated upwards can be calculated using:
Fnet=Fb−W=2mg−mg=mg
- The effective acceleration of the block relative to the water is:
ablock=Fnetm=g
- However, since the vessel is accelerating upwards, we need to consider the effective acceleration of the block relative to the upward acceleration of the vessel:
arelative=g−a0=g−g2=g2=5m/s2
4. Use Kinematic Equation to Find Time:
- The block starts from rest and moves a distance h=1.2m under the effective acceleration arelative=5m/s2.
- Using the kinematic equation:
h=12arelativet2
- Plugging in the values:
1.2=12⋅5⋅t2
- Rearranging gives:
t2=2⋅1.25=2.45=0.48
- Therefore, taking the square root:
t=√0.48≈0.693seconds
5. Final Calculation:
- The time taken by the block to reach the surface is approximately 0.693seconds.
Summary of the Solution:
The time taken by the block to reach the surface is approximately 0.693seconds.
- Specific gravity of the block, SG=0.5
- Depth of the block, h=1.2m
- Acceleration due to gravity, g=10m/s2
- Upward acceleration of the vessel, a0=g2=5m/s2
- The weight of the block W=m⋅g
- The volume of the block V=mρwood where ρwood=SG⋅ρwater=0.5⋅1000kg/m3=500kg/m3
- The buoyant force Fb=ρwater⋅V⋅g=1000⋅m500⋅g=2m⋅g
- The net force acting on the block when the vessel is accelerated upwards can be calculated using:
Fnet=Fb−W=2mg−mg=mg
- The effective acceleration of the block relative to the water is:
ablock=Fnetm=g
- However, since the vessel is accelerating upwards, we need to consider the effective acceleration of the block relative to the upward acceleration of the vessel:
arelative=g−a0=g−g2=g2=5m/s2
- The block starts from rest and moves a distance h=1.2m under the effective acceleration arelative=5m/s2.
- Using the kinematic equation:
h=12arelativet2
- Plugging in the values:
1.2=12⋅5⋅t2
- Rearranging gives:
t2=2⋅1.25=2.45=0.48
- Therefore, taking the square root:
t=√0.48≈0.693seconds
- The time taken by the block to reach the surface is approximately 0.693seconds.
The time taken by the block to reach the surface is approximately 0.693seconds.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A block of material of specific gravity 0.4 is held submerged at a depth of 1m in a vessel filled with water. The vessel is accelerated upwards with acceleration of ao=g/5. If the block is released at t = 0, neglecting viscous effects, it will reach the water surface at t equal to (g=10ms2) :
View SolutionA small block of wood of relative density 0.5 is submerged in water. When the block is released, it stats moving upwards, the acceleration of the block is (g=10ms−2)
View SolutionA small block of wood of density 0.4×103kg/m3 is submerged in water at a depth of 2.9m. Find
(a) the acceletation of the block towards the surface when the block is released and
(b) the time for the block to reach the surface, Ignore viscosity.
View SolutionAn open vessel containing the liquid upto a height of 15 m. A small hole is made at height of 10 m from the base of the vessel then the initial velocity of efflux is (g = 10 m/s2)
View SolutionA block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).
View SolutionThe elevator shown in figure is descending with an acceleration of 2ms2. The mass of the block A is 0.5 kg. What force is exerted by the block A on the block B?
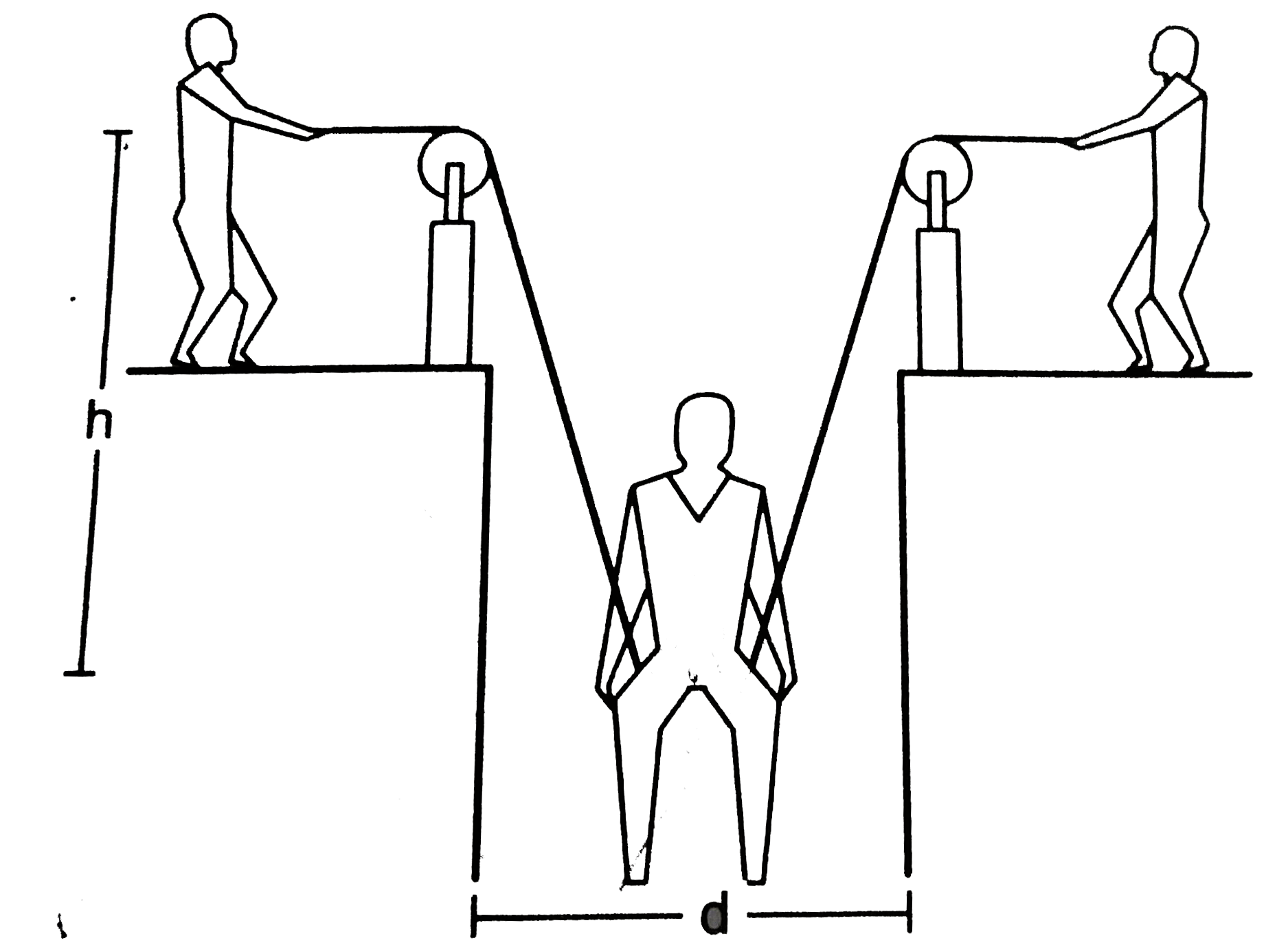
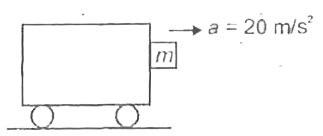
View SolutionA vehicle is moving on a road with an acceleration a=20m/s2 as shown in figure. The frictional coefficient between the block of mass (m) and the vehicle so that block is does not fall downward is (g=10m/s2)
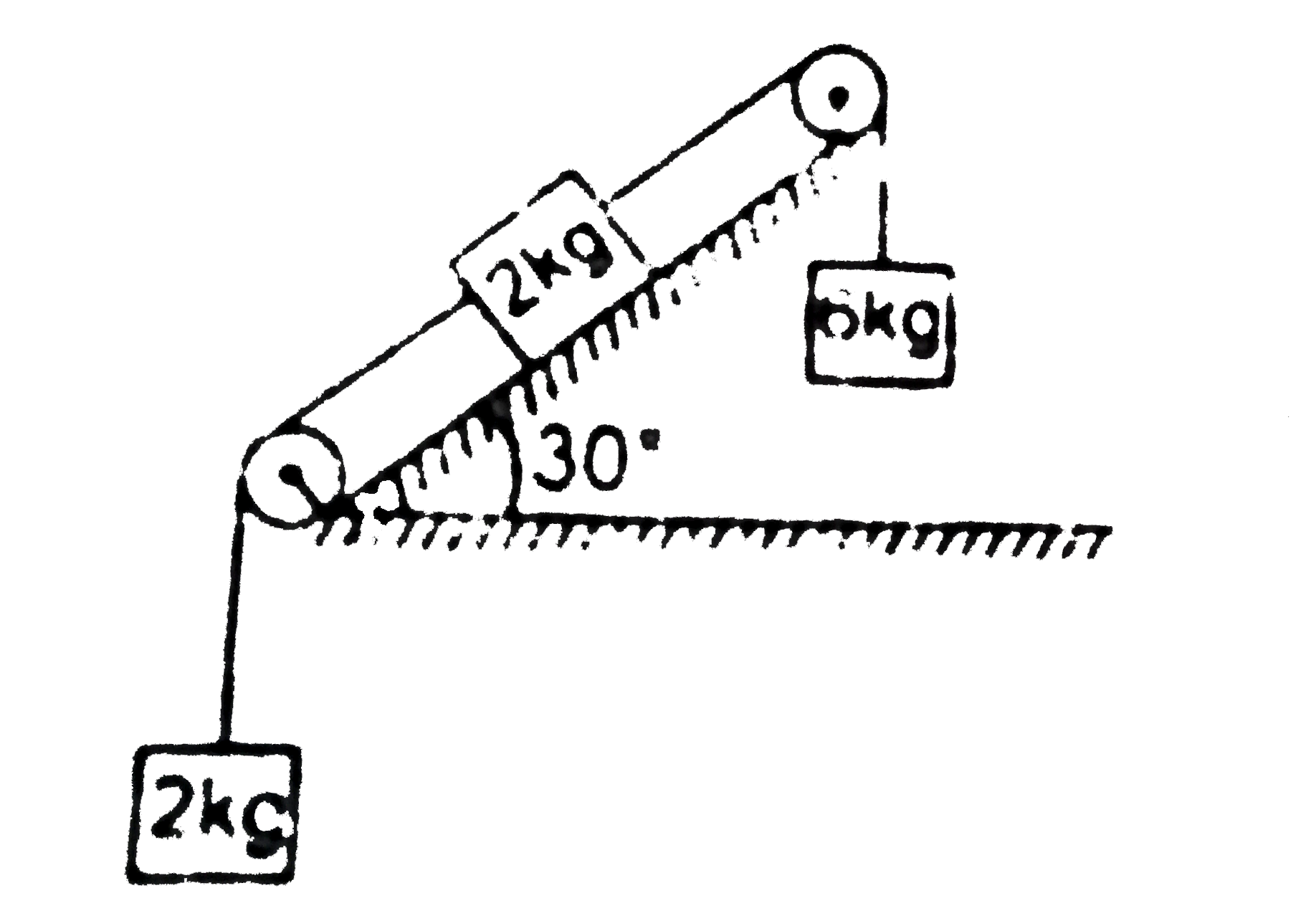
View SolutionFind the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
 .
.
View Solutiona block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12ms2. Find the displacement of the block during the first 0.2 s after the start. Take g=10ms2.
View SolutionA block is partially immeresed in a liquid and the vessel is accelerating upwards with an acceleration 'a'. The block is observed by two observers O1 and O2, one at rest and the other accelerating with an acceleration 'a' upward. The total buoyant force on the block is :
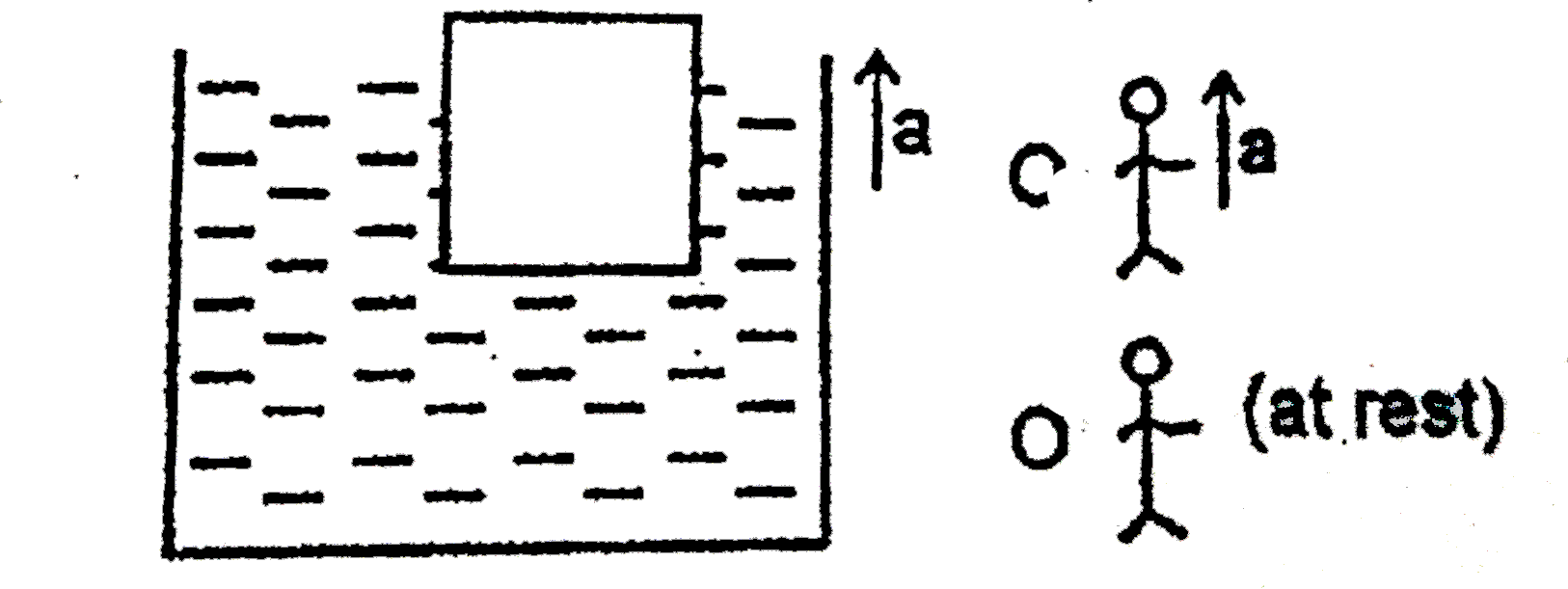
View Solution
