A load w is suspended from a wire of length l and area of cross-section A. Change in length of the wire is say Δl. Change in length Δl can be increased to two times by increasing
w by two times
l by two times
A by two times
A by four times
The correct Answer is:A, B
To solve the problem, we need to understand how the change in length (Δl) of a wire is affected by various parameters when a load (W) is applied. The relationship between the change in length of a wire and the parameters involved can be derived from Hooke's Law and the formula for stress and strain in materials.
1. Understanding the Relationship:
The change in length (Δl) of a wire under a load can be described by the formula:
Δl=W⋅lA⋅Y
where:
- W = Load applied
- l = Original length of the wire
- A = Cross-sectional area of the wire
- Y = Young's modulus of the material (a constant for a given material)
2. Doubling the Change in Length:
To increase the change in length (Δl) to two times its original value, we can manipulate the parameters in the equation. We want:
2Δl=W⋅lA⋅Y
3. Identifying Parameters to Change:
To achieve this, we can consider the following parameters:
- Increase the Load (W): If we double the load, the change in length will also double.
- Increase the Length (l): If we double the length of the wire, the change in length will also double.
- Decrease the Cross-sectional Area (A): If we reduce the area, the change in length will increase.
- Young's Modulus (Y): This is a material property and cannot be changed for a given material.
4. Conclusion:
From the analysis, we can conclude that to increase the change in length (Δl) to two times, we can either:
- Increase the load (W) to two times.
- Increase the length (l) to two times.
- Decrease the area (A) to half.
Therefore, the parameters that can be increased to achieve this are:
- Load (W)
- Length (l)
- Cross-sectional area (A) can be decreased.
Final Answer:
To double the change in length (Δl), you can increase:
- The load (W) to two times.
- The length (l) to two times.
- Decrease the cross-sectional area (A) to half.
The change in length (Δl) of a wire under a load can be described by the formula:
Δl=W⋅lA⋅Y
where:
- W = Load applied
- l = Original length of the wire
- A = Cross-sectional area of the wire
- Y = Young's modulus of the material (a constant for a given material)
To increase the change in length (Δl) to two times its original value, we can manipulate the parameters in the equation. We want:
2Δl=W⋅lA⋅Y
To achieve this, we can consider the following parameters:
- Increase the Load (W): If we double the load, the change in length will also double.
- Increase the Length (l): If we double the length of the wire, the change in length will also double.
- Decrease the Cross-sectional Area (A): If we reduce the area, the change in length will increase.
- Young's Modulus (Y): This is a material property and cannot be changed for a given material.
From the analysis, we can conclude that to increase the change in length (Δl) to two times, we can either:
- Increase the load (W) to two times.
- Increase the length (l) to two times.
- Decrease the area (A) to half.
- Load (W)
- Length (l)
- Cross-sectional area (A) can be decreased.
To double the change in length (Δl), you can increase:
- The load (W) to two times.
- The length (l) to two times.
- Decrease the cross-sectional area (A) to half.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Matrix Matching
12 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
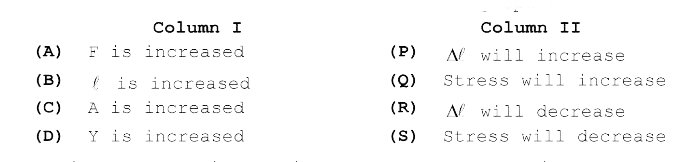
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
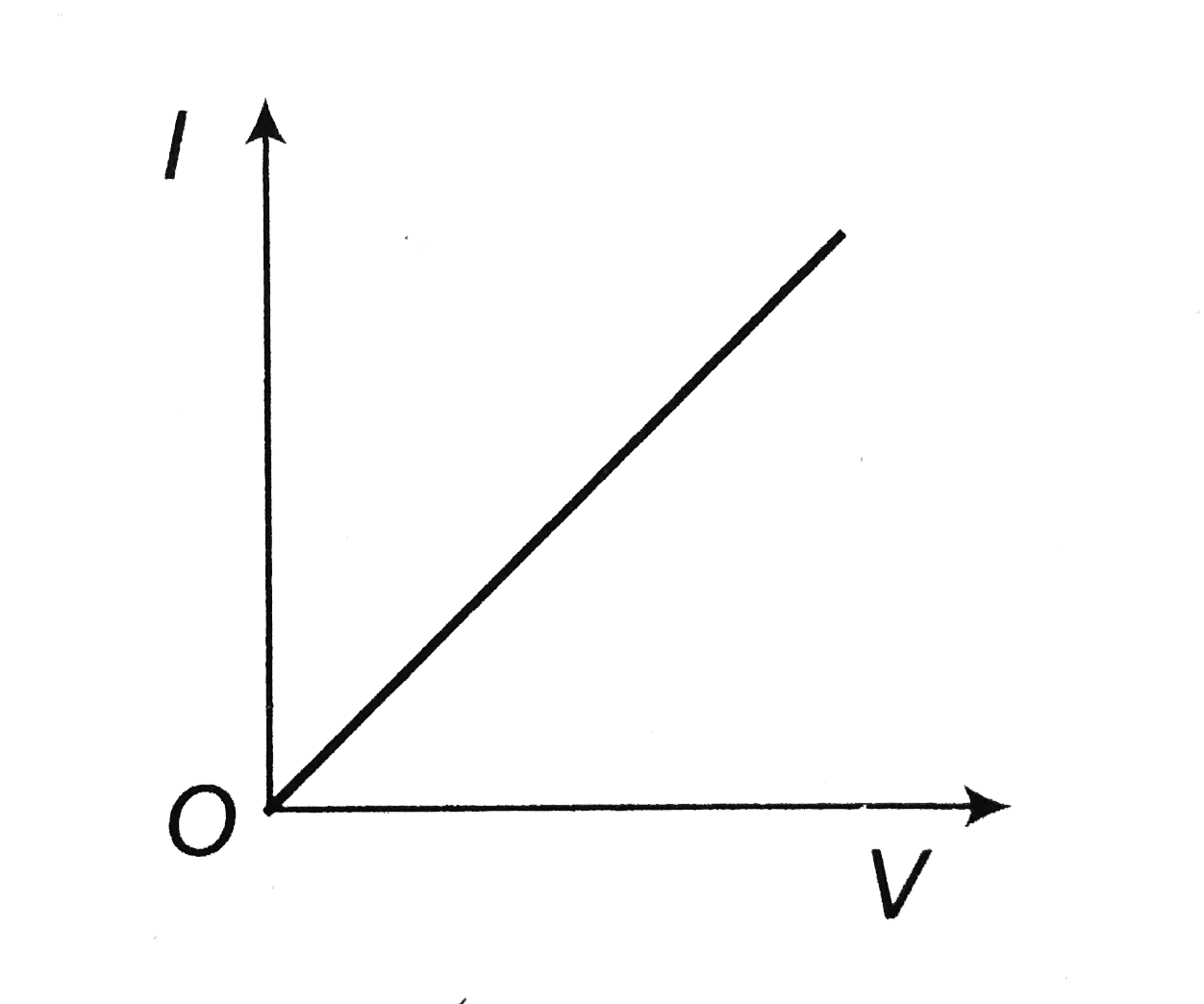
View SolutionI−V characterstic of a copper wire of length L and area fo cross-section A is shown in Fig. The slope of the curve becomes
View SolutionAn object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
View SolutionWhen a load of 10 kg is suspended on a metallic wire, its length increase by 2 mm. The force constant of the wire is
View SolutionA mass m is suspended from a wire . Change in length of the wire is Δl. Now the same wire is stretched to double its length and the same mass is suspended from the wire. The change in length in this case will become (it is suspended that elongation in the wire is within the proportional limit)
View Solution
