when a source of sound of frequency f crosses stationary observer with a speed vs(<< speed of sound v) , the apparent change in frequency Δf is given by
2fvsv
2fsvs
2fvsvs
fvsv
The correct Answer is:A
To solve the problem of finding the apparent change in frequency Δf when a source of sound of frequency f crosses a stationary observer with speed vs (where vs is much less than the speed of sound v), we can follow these steps:
1. Identify the Frequencies:
- The frequency of the source is f.
- When the source approaches the observer, the apparent frequency f1 is given by the formula:
f1=fvv−vs
- When the source moves away from the observer, the apparent frequency f2 is given by:
f2=fvv+vs
2. Calculate the Change in Frequency:
- The change in frequency Δf is defined as:
Δf=f1−f2
- Substituting the expressions for f1 and f2:
Δf=fvv−vs−fvv+vs
3. Factor Out f:
- We can factor f out of the equation:
Δf=f(vv−vs−vv+vs)
4. Combine the Fractions:
- To combine the fractions, we need a common denominator:
Δf=f(v(v+vs)−v(v−vs)(v−vs)(v+vs))
- Simplifying the numerator:
v(v+vs)−v(v−vs)=v2+vvs−v2+vvs=2vvs
- Thus, we have:
Δf=f(2vvs(v−vs)(v+vs))
5. Approximate for Small vs:
- Since vs is much smaller than v (i.e., vs≪v), we can approximate:
(v−vs)(v+vs)≈v2
- Therefore, the equation simplifies to:
Δf≈f(2vvsv2)=2fvsv
6. Final Result:
- The apparent change in frequency Δf is given by:
Δf=2fvsv
Summary:
The apparent change in frequency when a source of sound crosses a stationary observer is given by:
Δf=2fvsv
- The frequency of the source is f.
- When the source approaches the observer, the apparent frequency f1 is given by the formula:
f1=fvv−vs
- When the source moves away from the observer, the apparent frequency f2 is given by:
f2=fvv+vs
- The change in frequency Δf is defined as:
Δf=f1−f2
- Substituting the expressions for f1 and f2:
Δf=fvv−vs−fvv+vs
- We can factor f out of the equation:
Δf=f(vv−vs−vv+vs)
- To combine the fractions, we need a common denominator:
Δf=f(v(v+vs)−v(v−vs)(v−vs)(v+vs))
- Simplifying the numerator:
v(v+vs)−v(v−vs)=v2+vvs−v2+vvs=2vvs
- Thus, we have:
Δf=f(2vvs(v−vs)(v+vs))
- Since vs is much smaller than v (i.e., vs≪v), we can approximate:
(v−vs)(v+vs)≈v2
- Therefore, the equation simplifies to:
Δf≈f(2vvsv2)=2fvsv
- The apparent change in frequency Δf is given by:
Δf=2fvsv
The apparent change in frequency when a source of sound crosses a stationary observer is given by:
Δf=2fvsv
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Comprehion Type Questions
20 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS
50 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
(A) : When a source moves towards a stationary observer, the speed of source relative to the observer remains unchanged.
(R): The apparent change in frequency is due to change in the wavelength brought by the motion of the source.
View Solutionthe frequency changes by 10 % as the source approaches a stationary observer with constant speed vs. What would be the percentage change in frequency as the sources reaccedes the observer with the same speed ? Given , that vs<<v(v= speed pf sound in air )
View Solution
Knowledge Check
A sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
A109B(109)2C(1110)2D1110An observer moves towards a stationary source of sound. The percentage change in the apparent frequency is
AzeroB0.05C0.1D0.2
When both source and observer approach each other with a speed a equal to the half the speed of sound, then determine the percentage change in frequency of sound as detected by the listener.
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA source of sound and an observer are approaching each other with the same speed, which is equal to (110) times the speed of sound. The apparent relative change in frequency of source is
View SolutionA driver is riding a car with velocity vc between two vertical walls on a horizontal surface as shown in figure.A source of sound of frequency 'f' is situated on the car. (vc<<v, where v is the speed of sound in air )

Beat frequency observed by the driver corresponding to sound waves reflected from wall-1 amd wall-2 (reflected waves corresponding to waves directly coming from source ):
View SolutionWhen a source of frequency f0 moves away from a stationary observer with a certain velocity, an apparent frequency f' is observed. When it moves with the same speed towards the observer, the observed frequecy is 1.2f'. If the velocity of sound is v, then the acutual frequency f0 is
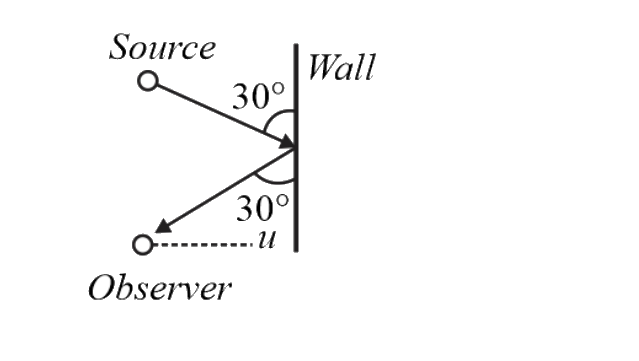
View SolutionA stationary source (see figure) emits sound waves of frequency f towards a stationary wall. If an observer moving with speed u in a direction perpendicular to the wall measures a frequency f'=118f at the instant shown, then u is related to the speed of sound Vs as
View Solution
